Теорема Кельвина о безвихревом движении

В 1849 году Уильям Томсон доказал теорему о минимальной кинетической энергии жидкости:

если на границе некоторой односвязной области вихревое движение совпадает с безвихревым, то кинетическая энергия безвихревого движения в рассматриваемой области меньше кинетической энергии вихревого движения.

[Править] Доказательство первой теоремы Кельвина

Теорему Кельвина можно доказать, основываясь на том, что скорость в безвихревом движении потенциальна (v = gradφ) и что дивергенция скорости несжимаемой жидкости равна нулю, как для безвихревого, так и для вихревого движения. В самом деле, пусть ΔЧто-то = Что-то_вихр. − Что-то_{безвихр.}. Тогда для разности кинетических энергий можно записать:

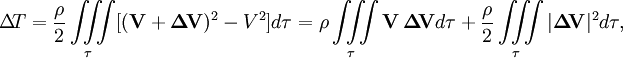
где ρ — плотность жидкости, а τ — жидкий объём. Рассмотрим далее только первый интеграл справа:

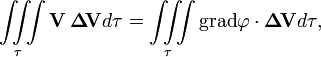
а, так как div(φa) = φ diva + gradφ·a, интеграл можно преобразовать так:

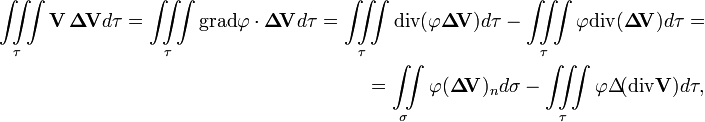
где σ — поверхность, ограничивающая объем τ, а индекс n обозначает нормальную составляющую вектора. Из условия теоремы следует, что на поверхности σ вихревое и безвихревое движения совпадают, т. е. ΔV = 0, кроме того по условию несжимаемости div V = 0. Таким образом, в последнем равенстве все слагаемые равны нулю и для разности кинетических энергий получается:

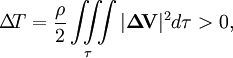
из чего и следует теорема Кельвина.

[править] Кинематическая теорема Кельвина

Кинематическая теорема Кельвина позволяет с чисто кинематической стороны предсказать поведение вихревой трубки во времени. Формулировка теоремы такова:

частная производная по времени от циркуляции скорости по замкнутому жидкому контуру равна циркуляции ускорения по этому же контуру.

[править] Доказательство второй теоремы Кельвина

Вычислим частную производную по времени от циркуляции скорости по произвольному контуру C, не делая для начала предположения о его замкнутости.

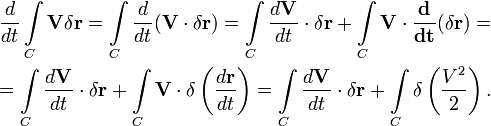
Очевидно, при замыкании контура последний интеграл обратится в нуль. Таким образом:

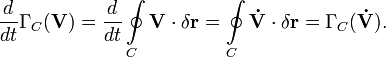
[править] Теорема Кельвина о баротропной жидкости

Теорему Кельвина о баротропной жидкости также называют основной теоремой Кельвина, которая обосновывает возможность существования безвихревого движения:

при баротропном движении жидкости идеальной жидкости под действием потенциальных сил циркуляция скорости по замкнутому жидкому контуру не изменяется.

[править] Доказательство третьей теоремы Кельвина

Теорема легко доказывается на основе предыдущей теоремы подстановкой в правую часть выражения для ускорения в случае потенциальных сил: :

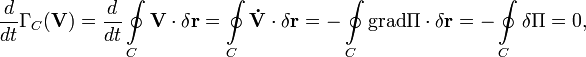
следовательно, Г — постоянная величина.

Теорема была сформулирована и доказана У. Томсоном в 1869 году.

Три теоремы Гельмгольца о вихрях.

Теорема разложения Гельмгольца

[править]

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

Теорема разложения Гельмгольца — утверждение о разложении произвольного дифференцируемого векторного поля на две компоненты:

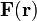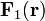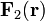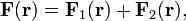
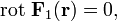
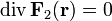
Если дивергенция и ротор векторного поля определен в каждой точке конечной открытой области V пространства, то всюду в V функция может быть представлена в виде суммы безвихревого поля и соленоидального поля : где для всех точек 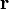области V.

Содержание [убрать] 1 Формулировка теоремы 2 Поля, определенные ротором и дивергенцией 3 Примечания 4 Литература 5 См. также