42. Условный экстремум с ограничениями типа неравенств. Необходимые условия экстремума первого и второго порядка. Пример.
Пусть требуется исследовать функцию на экстремум, т.е. определить точки ее локальных минимумов и максимумов , где .
Необходимые
условия минимума (максимума) первого
порядка. Пусть
− точка локального минимума (максимума)
в задаче. Тогда найдется такое число
,
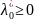и вектор
,
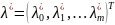не равные одновременно нулю и такие,
что выполняются следующие условия:
стационарности обобщенной функции Лагранжа по x
допустимости решения
неотрицательности для условного минимума
дополняющей нежесткости
Если
в задаче ограничения записаны в форме
то их необходимо переписать как
.
При
необходимые условия минимума (максимума)
первого порядка для выпуклых функций
(
)
будут одновременно и достаточными
условиями глобального минимума
(глобального максимума).
Из
условия дополняющей нежесткости следует,
что если ограничение в точке
пассивное, т.е.
,
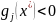то
,
а если активное, т.е.
,
то
(для минимума), и
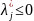(для максимума).
Необходимые
условия минимума (максимума) второго
порядка. Пусть
− точка локального минимума (максимума)
в задаче и имеется решение
системы необходимого условия первого
порядка. Тогда второй дифференциал
классической функции Лагранжа, вычисленный
в точке
,
неотрицателен (неположителен) для всех
таких, что
.
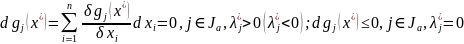43. Условный экстремум с ограничениями типа неравенств. Достаточные условия экстремума первого и второго порядка. Пример.
Достаточные
условия минимума (максимума) первого
порядка. Пусть имеется точка
,
удовлетворяющая системе необходимого
условия первого порядка при
,
число активных ограничений в точке
совпадает с числом n
переменных (при этом условие регулярности
выполняется). Если
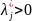для всех
,
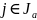то
− точка условного локального минимума.
Если
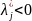для всех
,
то
− точка условного локального максимума
в задаче.
Достаточные
условия минимума (максимума) второго
порядка. Пусть имеется точка
,
удовлетворяющая системе необходимого
условия первого порядка при
.
Если в этой точке
,
(соответственно,
)
для всех ненулевых
таких, что
,
то
− точка локального минимума (максимума)
в задаче.
Алгоритм решения задачи.
Шаг 1. Составить обобщенную функцию Лагранжа
Шаг 2. Записать необходимые условия минимума (максимума) первого порядка
а)
б)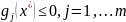
в)
(для минимума),
(для максимума)
г)
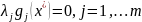
Шаг 3. Решить систему для двух случаев
1)
2) (при этом поделить условие а) на и заменить на )
В результате найти условно-стационарные точки , выделив из них полученные при (они могут быть регулярными точками экстремума).
В
каждом из двух случаев следует начинать
с рассмотрения
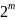вариантов удовлетворения условия "г"
дополняющей нежесткости.
Шаг 4. Для выделенных на шаге 3 точек проверить достаточные условия экстремума первого или второго порядка.
Для проверки достаточных условий первого порядка следует:
а) определить число l активных в точке ограничений;
б)
если
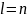и для всех
,
то в точке
− локальный минимум; если
и
для всех
,
то в точке
− локальный максимум. Если
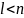или соответствующие множители
Лагранжа не удовлетворяют достаточным
условиям первого порядка, то проверить
достаточные условия второго порядка.
Для проверки достаточных условий второго порядка следует:
а)
записать выражение для второго
дифференциала классической функции
Лагранжа в точке
:
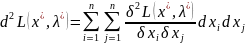
б)
записать условия, накладываемые на
первые дифференциалы активных ограничений:
в) исследовать знак второго дифференциала функции Лагранжа для ненулевых , удовлетворяющих системе выше. Если , то в точке − условный локальный минимум. Если , то в точке − условный локальный максимум.
Если достаточные условия первого и второго порядка не выполняются, следует проверить выполнение необходимых условий второго порядка, следуя аналогичной процедуре. Если они выполняются, то требуется дополнительное исследование, а если нет, то в точке нет условного экстремума.
Шаг 5. Вычислить значения функции в точках условного экстремума.