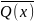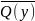Логика предикатов

Одноместным предикатом P(x) называется всякая функция одного переменного, в которой x пробегает значения из некоторого множества M, а функция при этом принимает значения 0 или 1.

Множество M, на котором задан предикат, называется областью определения предиката.

Множество I_p c M, на котором предикат принимает только истинные значение, называется областью истинности предиката P(x).

Предикат P(x) называется ТИ (ТЛ) на множестве M, если I_p Ξ M (I_p = ).

n-местным предикатом на множестве M называется функция P(x₁, x₂, …, x_n), имеющая тип 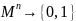, где аргумент – вектор длины n с компонентами из множества M, а значением 0 или 1.

Множество M – предметное множество. Предикаты обозначаются большими буквами латинского алфавита.

P, Q, R, Z – предикатные переменные

p, q, r, z – предметные переменные

При n = 1 одноместный предикат P(x) называют свойством.

При n = 2 двуместный предикат P(x) называют отношением.

Операции над предикатами

P(x) v Q(x)	P(x) v Q(y)
P(x) Λ Q(x)	P(x) Λ Q(y)
P(x) -> Q(x)	P(x) -> Q(y)
P(x) <--> Q(x)	P(x) <-> Q(y)

x P(x) – будем обозначать таким образом высказывание, которое истинно тогда и только тогда, когда P(x) = 1 для любых x, т. е. предикат P(x) принимает значение истина для всех x из предметной области.

P(x) не высказывание.

x P(x) – высказывание.

x P(x) – будем обозначать таким образом высказывание, которое ложно тогда и только тогда, когда P(x) = 0 при всех x из предметной области.

Операция навешивания квантора на переменную называется связыванием, и понижает мощность предиката на 1.

Символом x обозначается n-местный предикат на множестве M, зависящий от x₁, x₂, …, x_n и не зависящий от x. Он принимает значение 1 для тех и только тех векторов (a₁, a₂, …, a_n), для которых одноместный предикат P(x, a₁, …, a_n) тоже является истинным на M.

x P(x, x₁, …, x_n) называется n-местным на мн-ве M, зависит от x₁, x₂, …, x_n и не зависит от x. Он принимает значение 0 для тех векторов (a₁, a₂, …, a_n) из M, для кот-х предикат P(x, a₁, a₂, …, a_n) = 0 на M.

Определение формулы логики предикатов (лп):

1. Каждое высказывание, как переменные, так и постоянные, является формулой.

2. Если P – символ предиката, а x₁, x₂, …, x_n – предметные переменные или предметные константы, то P(x₁, x₂, …, x_n) – формула. Такая формула элементарная, в ней предметные переменные свободны, не связаны кванторами.

3. Если A, B – формулы, то A Λ B, A v B, 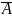, A -> B, A <--> B тоже формулы.

4. Если A(x) – формула, в которой переменная x входит свободно, то x A(x), x A(x) – формулы, предметная переменная входит связанно.

5. Других формул нет.

Из определения формулы ЛП ясно, что всякая формула АВ является формулой алгебры предикатов.

Логическое значение формулы ЛП зависит от значений 3-х переменных:

1) значений, входящих в формулу, переменных высказываний;

2) значений свободных предметных переменных на M;

3) значений предикатных переменных.

При конкретных значениях каждого из 3-х видов переменных формула ЛП становится высказыванием, имеющим истинное или ложное значение.

Две формулы ЛП A и B называются равносильными на области M, если они принимают одинаковые логические значения входящих в них переменных, отнесенных к области M.

Две формулы ЛП A и B называются равносильными, если они равносильны на всякой области (A=B).