4. Преобразования Галилея. Принцип относительности Галилея.

Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой^[1]. Термин был предложен Филиппом Франком в 1909 году.^[2] Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время»^[3]) и выполнение принципа относительности (принцип относительности Галилея (см. ниже)).

• Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.

Вид преобразований при коллинеарных осях^[4]

Если ИСО S движется относительно ИСО S' с постоянной скоростью вдоль оси , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:

или, используя векторные обозначения,

(последняя формула остается верной для любого направления осей координат).

• Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).

Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:

• Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей 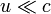(много меньше скорости света).

Формула преобразования скоростей

Достаточно продифференцировать в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.

Приведем более элементарный, но и более общий вывод — для случая произвольного движения начала отсчета одной системы относительно другой (при отсутствии вращения). Для такого более общего случая, можно получить формулу преобразования скоростей, например, так.

Рассмотрим преобразование произвольного сдвига начала отсчета на вектор ,

где радиус-вектор какого-то тела A в системе отсчета K обозначим за , а в системе отсчета K' — за ,

подразумевая, как всегда в классической механике, что время t в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени: .

Тогда в любой момент времени

и в частности, учитывая

,

имеем:

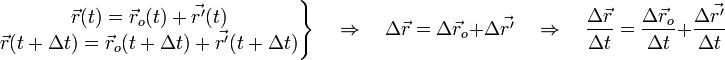
где:

— средняя скорость тела A относительно системы K;

— средняя скорость тела А относительно системы K' ;

— средняя скорость системы K' относительно системы K.

Если то средние скорости совпадают с мгновенными:

или короче

— как для средних, так и для мгновенных скоростей (формула сложения скоростей).

Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга:

Принцип относительности Галилея

Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, то есть , то ускорение тела относительно обеих систем отсчета одинаково.

Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль (см.второй закон Ньютона), то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-то конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна

Иным образом этот принцип формулируется (следуя Галилею) так: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.

Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, во многом следует форма и структура ньютоновской механики (и исторически также они оказали существенное влияние на ее формулировку). Говоря же несколько более формально, они налагают на структуру механики ограничения, достаточно существенно влияющие на ее возможные формулировки, исторически весьма сильно способствовавшие ее оформлению.