Механика

1. Кинематика поступательного движения математической точки

2. Кинематика вращательного движения математической точки.

3. Принцип инерции Галилея. Законы Ньютона.

4. Преобразования Галилея. Принцип относительности Галилея.

5. Теорема о кинетической энергии тела. Закон сохранения механической энергии.

6. Импульс тела. Закон сохранения импульса.

7. Момент импульса. Закон сохранения момента импульса.

8. Момент силы. Основной закон механики вращательного движения.

9. Определение периода колебаний математического маятника. Гармонические колебания.

10. Определение периода колебаний физического маятника.

11. Основное уравнение МКТ. Уравнение Менделеева-Клайперона.

12. I начало термодинамики. Изопроцессы.

14. Уравнение адиабаты. Адиабатический процесс. Коэффициент Пуассона.

15. Работа газа в изопроцессах.

16. Статический вес. Энтропия. III начало термодинамики.

17. Процессы переноса. Диффузия. Теплопроводность. Внутреннее трение.

Электромагнетизм

18. Напряженность и потенциал электростатического поля. Принцип суперпозиции.

19. Электрический диполь. Механический вращающийся момент.

20. Теорема Гаусса. Циркуляция и ротор электростатического поля.

21. Циркуляция вектора. Ротор. Теорема Стокса.

22. Поток вектора. Дивергенция. Теорема Остроградского-Гаусса.

23. Вектор электрического смещения. Поляризация диэлектрика.

24. Магнитное поле движущегося заряда. Закон Био-Савара-Лапласа.

25. Дивергенция и ротор магнитного поля.

26. Поле соленоида и тороида.

27. Магнитное поле в магнетиках. Намагниченность Напряженность магнитного поля.

28. Ферромагнетики. Магнитный гистерезис. Магнитная проницаемость ферромагнетиков.

29. Закон электромагнитной индукции. Самоиндукция. Энергия магнитного поля. Индуктивность.

30. Контур с током в магнитном поле(Вращающийся момент и энергия).

31. ЭДС сторонних сил. Напряжение. Закон Ома для неоднородного участка цепи.

32. Закон Джоуля-Ленца. Законы Кирхгофа для постоянного тока.

33. Вихревое электрическое поле. Ток смещения.

34. Уравнение Максвелла и их физический смысл.

Оптика

35. Волновое уравнение электромагнитных волн. Плоская электромагнитная волна. Вектор Умова-Пойнтинга.

36. Законы геометрической оптики. Принцип Гюйгенса. Принцип Ферма.

37. Тонкая линза. Формула тонкой линзы.

38. Интерференция света. Условия интерференционных максимумов, минимумов.

39. Дифракция. Принцип Гюйгенса-Френеля.

40. Метод зон Френеля. Дифракция на узкой щели.

41. Дифракционная решетка.

Ответы

1. Кинематика поступательного движения математической точки

Основные кинематические понятия

Поступательным движением твердого тела называют такое его движение, при котором каждая линия, соединяющая две любые точки тела, сохраняет неизменное направление в пространстве. Например, вагон, движущийся по прямому участку пути; кабина колеса обозрения и др.

Материальная точка  — тело, размерами которого по сравнению с характерными расстояниями данной задачи можно пренебречь. Так Землю можно считать Материальной Точкой (М. Т.) при изучении её движения вокруг Солнца, пулю можно считать М. Т. при её движении в поле тяжести Земли, но нельзя считать таковой при учете её вращательного движения в стволе винтовки. При поступательном движении в ряде случаев при помощи понятия М. Т. можно описывать и изменение положения более крупных объектов. Так, например, тепловоз, проходящий расстояние 1 метр, может считаться М. Т., поскольку его ориентация относительно системы координат в процессе движения является фиксированной и не влияет на постановку и ход решения задачи.

Радиус-вектор — Вектор, определяющий положение М. Т. в пространстве:  . Здесь r₁,r₂,...,r_n — координаты радиус-вектора. Геометрически изображается вектором, проведенным из начала координат к материальной точке. Зависимость радиус-вектора (или его координат r_i = r_i(t)) от времени   называется законом движения.

Траектория — Годограф радиус-вектора, то есть — воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется М. Т. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием, длиной пути или вульгарно — путем и обозначают буквой S. При таком описании движения S выступает в качествеобобщенной координаты, а законы движения в этом случае записывается в виде S = S(t) и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде:

,

Где :   — модуль начальной скорости, а a_S = a_τ — Тангенциальное ускорение.

Описание движения при помощи понятия траектории — один из ключевых моментов классической механики . В квантовой механике движения носит бестраекторный характер, а само понятие траектории теряет смысл.

Основные кинематические величины

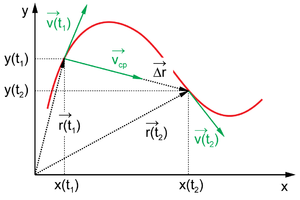
Радиус-вектора и вектор перемещения (черные стрелки). Вектора средней и мгновенных скоростей (Зеленые стрелки). Траектория (красная линия)

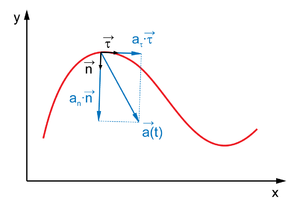
Разложение ускорения по сопутствующему базису

Перемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:

.

Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени.

Средняя скорость — векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:

.

Мгновенная скорость — векторная физическая величина, равная первой производной от радиус-вектора по времени:

.

Характеризует быстроту перемещения материальной точки. Мгновенную скорость можно определить как предел средней скорости при устремлении к нулю промежутка времени, на котором она вычисляется:

.

Единица измерения скорости в системе СИ— м/с, в системе СГС — см/с. Мгновенная скорость всегда направлена по касательной к траектории.

Мгновенное ускорение — векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:

.

Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормального и тангенциального ускорения:

.

Здесь   — единичный вектор нормали,   — единичный вектор касательной. Величина a_n называется нормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории:

.

В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности.

Величина a_τ называется тангенциальным ускорением и характеризует величину изменения модуля скорости:

.