* 38). Частица в потенциальном ящике с бесконечно высокими стенками
Будем считать: *что частица может двигаться только в направлении оси ОХ.
*стенки ямы бесконечно высокие и представляют собой параллельные плоскости
Пусть движение ограничено непроницаемыми для частицы стенками.
Такая
яма описывается потенциальной энергией
вида
Где
-
ширина «ямы» и энергия отсчитывается
от её дна.
П
отенциальная
энергия частицы в ящике равна нулю, а
за пределами ящика
.
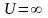Ур.
Шредингера для
такой частицы
эн.
частицы в ящике
При n=1 вероятность обнаружить частицу в яме максимальная, а по краям ямы = 0
При n=2 частица не может быть обнаружена в середине ямы, однако она одинаковое число раз бывает в левой и правой частях.
*39). Движение частицы в потенциальном ящике конечной глубины
П
отенциальная
энергия частицы: *в ящике
при
,
*вне ящика
при
Примером такой ситуации является движение коллективизированных электронов внутри металла.
Применим к частице в таком потенциальном ящике уравнение Шредингера
В
области I
.
В области II
*
40).
Прохождение частицы через потенциальный
барьер
Рассмотрим
частицу, которая движется слева на
право, встречая на своем пути потенциальный
барьер высоты U0
и ширины l
можно записать:
*
Если
то частица беспрепятственно проходит
над барьером *Если же E
меньше U0,
то частица отражается от барьера и летит
обратно
Туннельный эффект - преодоление микрочастицей потенциального барьера в случае, когда её полная энергия меньше высоты барьера.
*41).
Гармонический
осциллятор
– частица, совершающая одномерное
движение под действием квазиупругой
силы
с потенциальной энергией как у
классического осциллятора.
*42). Модель атома резерфорда (космическая модель)
*
Любой
атом состоит
из положительно заряженного ядра и
окружающей его электронной
оболочки.
*Размеры ядра менее 10-12 см, размеры же самого атома, определяемые электронной оболочкой, порядка 10-8 см, т. е. в десятки тысяч раз больше размеров ядра.
*При этом практически вся масса атома сосредоточена в ядре.
В своих рассуждениях Резерфорд принимал во внимание рассеяние α-частиц только на ядрах, поскольку заметного отклонения α-частиц электронами не может быть из-за того, что масса электронов на четыре порядка меньше массы α-частиц.
Когда α-частица пролетает вблизи ядра, *ее траектория представляет собой гиперболу *причем угол отклонения α-частицы — угол θ — равен углу между асимптотами гиперболы
Для
угла θ
было получено выражение
*43). Постулаты Бора. 1). постулат стационарных состояний: Атом может длительное время находиться только в определенных, которые характеризуются дискретными значениями энергии E1, E2, Е3, ... В этих состояниях, атом не излучает.
2). Правило частот: при переходе атома из стационарного состояния в другое происходит, излучение фотона: ħω =E2-E1.
Опыты Франка и Герца дали прямое доказательство дискретности атомных состояний
Идея
опытов:
*При неупругих столкновениях электрона
с атомом происходит передача энергии
от электрона атому.
*Если внутренняя энергия атома изменяется
непрерывно,
то атому может быть передана любая
порция энергии.
Боровская модель атома водорода Бор предположил, что электрон в атоме водорода движется только по тем круговым орбитам, для которых его момент импульса M=nħгде n — квантовое число.
С помощью этого правила квантования можно найти радиусы круговых стационарных орбит водородоподобных систем (Н, Не+, Li++...) и соответствующие им энергии.
44). Квантово-механическая модель строения атома
В основу КММ положена квантовая теория атома, согласно которой электрон обладает как свойствами частицы, так и свойствами волны. Т.е. о местоположении электрона в определенной точке можно судить не точно, а с определенной долей вероятности. Поэтому в КММ орбиты Бора заменили орбиталями (эдакие "электронные облака" - области пространства в которых существует вероятность пребывания электрона). Состояние электрона в атоме описывают с помощью 4 квантовых чисел: 1). n-главное (энергетический уровень орбитали, 1, 2, 3...) 2). L-орбитальное (Форма орбитали, от 0 до n-1) 3). M-квантовое (ориентация, -1 до +1) 4). ms – Спиновое (Спин электрона, +½ и -½)