3.2 Геометрическая интерпретация векторов Ортононормированный базис в пдск

Если заданы векторы такие, что

-

- все три имеют общим началом начало координат;

- каждый из векторов сонаправлен -

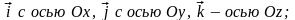
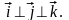- (см. Рис.24)

Рис.24

Теперь понятно, что значит «ортонормированный»:

- «орто» - все три вектора взаимно перпендикулярны или, что тоже самое, ортогональны;

- «нормированный» - все они «нормированы на единицу», т.е. имеют одинаковую, равную единице длину.

А вот «базис» означает то, что любой вектор может быть представлен в виде суммы проекций на соответствующие оси, т.е. может быть произведено разложение вектора по ортонормированному базису.

Разложение вектора по ортонормированному базису

Любой вектор в ПДСК может быть разложен на сумму его проекций на оси координат:

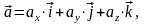
где a_x, a_y, a_z – величины проекций вектора 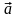на соответствующие оси координат. Уж, коль скоро, речь идет о «величине», то она, как и величина отрезка, может быть и положительной и отрицательной. Наряду с термином «величина проекции» используется и термин «координата вектора». Второй термин вполне приемлем, но, в отличии от первого часто создает путаницу. Разберемся с этой путаницей раз и (мы надеемся!) навсегда.

Нахождение координат вектора

Найти координаты вектора , если M₁(x₁; y₁; z₁) и M₂(x₂; y₂; z₂). Для того, что бы найти величину проекции на ось необходимо вычесть из координат конца координаты начала вектора. В нашем случае

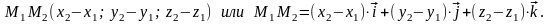
Нагляднее всего это продемонстрировать с вектором на плоскости.

Пример 24(координаты вектора на плоскости)

Найти координаты вектора , если он имеет своим началом точку М₁, а концом точку М₂, если он изображен на Рис.25.

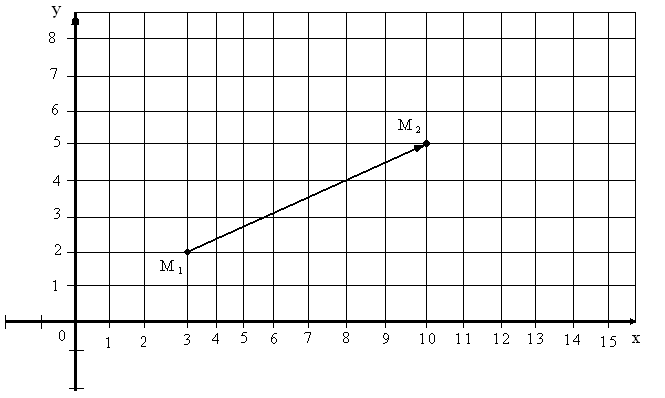
Рис.25

Решение

Из чертежа видно, что точка М₁ имеет координаты x₁ = 3, y₁ =2, т.е. М₁(3; 2) и точка М₂(10; 5), тогда вектор имеет координаты

,

или, окончательно

Ответ

Свободные векторы

Свободный вектор – вектор, который вполне определен своими координатами: он не привязан ни к какой точке пространства и при параллельном переносе (с сохранением направления и длины) его координаты не изменяются. Если вектор задан в координатной форме, то никто не скажет, где он расположен.

Пример 25 (свободные векторы)

На рисунке 26 представлены три вектора. Один из них – вектор уже был рассмотрен в Примере 24.

Рис.26

Не трудно убедиться в том, что

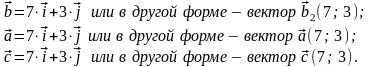
3.3 Основные арифметические действия над векторами

Здесь и далее предполагается, что векторы заданы в координатной форме

Длина вектора

Длина вектора определяется выражением

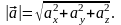
Скалярное произведение (координатная форма)

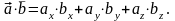
Угол между векторами

Если φ – угол между векторами , то

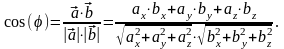
Условие ортогональности векторов

Два вектора ортогональны при условии равенства нулю их скалярного произведения

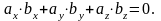
Сумма (разность) векторов

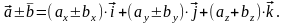
3.4 Векторное произведение векторов

Векторным произведением векторов называется вектор, обозначаемый символом ( или ), который определяется условиями

1. , где φ – угол между векторами ;

2. вектор 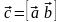такой, что 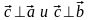одновременно;

3. вектор ориентирован по отношению к сомножителям по правилу буравчика.

Правило буравчика

Вектор , как результат векторного произведения ориентирован по отношению к сомножителям так же, как координатная ось Oz по отношению к осям Ox и Oy (cм. Рис. 27). Т.е., при вращении от первого сомножителя ко второму буравчик ввинчивается в направлении вектора .

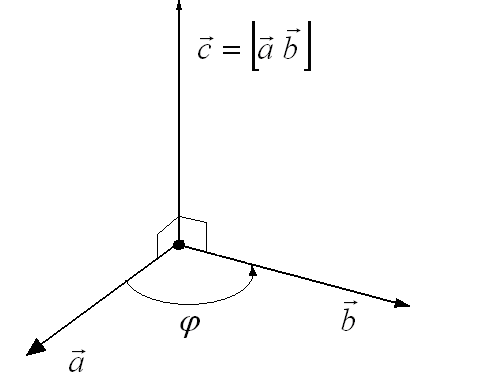
Рис.27

Условие коллинеарности векторов

Если векторы коллинеарны (лежат на одной прямой или на параллельных прямых) т.е. угол между ними или 0, или 180⁰, то их векторное произведение равно нулю

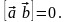
Геометрический смысл векторного произведения

Если векторы приведены к общему началу (что параллельным переносом возможно сделать всегда, поскольку мы работаем только со свободными векторами), то длина вектора равна площади параллелограмма, построенного на перемножаемых векторах (см.Рис.28).

Рис.28

Свойства векторного произведения

1. Свойство антикоммутативности

2. Свойство ассоциативности по отношению к скалярному множителю λ

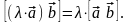
3. Распределительное свойство относительно операции сложения

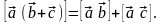
Пример 26 (раскрытие скобок в выражении с векторами)

Раскрыть скобки в выражении

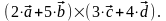
Решение

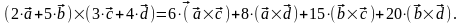
Пример 27 (вычисление площади параллелограмма)

Вычислить площадь параллелограмма, построенного на векторах 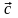и , если

;

;

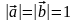Решение

Прежде всего, площадь параллелограмма, построенного на векторах и , определяется как

.

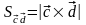Т.е. найдем векторное произведение векторов c и d, а потом длина полученного вектора численно будет равна искомой площади параллелограмма.

Шаг 1

Ищем векторное произведение, при этом активно используем свойства векторного произведения

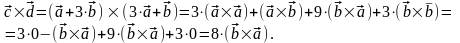
Шаг 2

Ищем, собственно площадь