4. Векторы

Представление о векторах как о направленном отрезке на много менее эффективно и продуктивно, чем алгебраическая интерпретация векторов.

3.1 Алгебраическая интерпретация векторов

Упорядоченный одномерный упорядоченый массив из n чисел x₁, x₂, x₃…x_n называется n-мерным вектором, сами числа x₁, x₂, x₃…x_n при этом называются координатами вектора.

Пример 21 (алгебраический вектор)

Некоторое предприятие специализируется на выпуске n видов продукции. За некоторый период выпущено x₁ единиц продукции первого типа, x₂ единиц второго типа и т.д. Т.о. образован вектор

X = (x₁, x₂, x₃…x_n).

Вектор X при этом называется вектором выпуска продукции.

Как только мы определили вектор упорядоченный одномерный массив чисел, так сразу же мы дали себе право рассматривать вектор как матрицу размерности или . А это дает нам право применять к ним всю мощь матричной алгебры: понятия равенства, суммы или разности, произведение вектора на число и их свойства не надо рассматривать вновь, достаточно вспомнить, как это делалось в разделе «Линейная алгебра».

Но операцию умножения имеет смысл рассмотреть особо.

Скалярное произведение векторов

Пусть векторы X и Y заданы в алгебраической форме, тогда их скалярным произведением назовем число равное сумме произведений соответствующих координат, т.е. если

X = (x₁, x₂, x₃…x_n)

Y = (y₁, y₂, y₃…y_n),

т.о., скалярное произведение X∙Y определяется выражением

Замечание к определению скалярного произведения

Очень часто скалярное произведение векторов 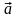и определяют как

,

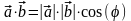где 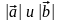- длины векторов, а φ угол между векторами, откуда, как следствие определяется угол между векторами.

Угол между векторами

Казалось бы, вполне симпатичное определение, но… Такое определение работоспособно, как правило, только для векторов, определенных как «направленный отрезок»: длину измерили линейкой, а угол – транспортиром. А как быть с алгебраическим вектором (чаще всего именно он используется в не инженерно-физических задачах), где координат может быть много и никакой линейкой их длину не измерить?! Вот здесь-то и становится необходимым то определение скалярного произведения, которое дали мы.

Пример 22 (скалярное произведение и общая цена выпущенной продукции)

Пусть некоторое предприятие выпустило партию товара n видов в количествах x₁, x₂, x₃,…, x_n каждого вида. Цена единицы каждого вида товара равна y₁, y₂, y₃,…,y_n рублей. Какова цена всей партии товара?

Решение

Идея решения понятна: умножить цену единицы каждого вида товара на количество этих единиц, а потом все эти произведения сложить. Но уже здесь видна продуктивность данного выше определения скалярного произведения векторов: сумма произведений соответствующих координат. А потому сформируем два вектора:

- вектор X = (x₁, x₂, x₃,…, x_n) – вектор выпуска продукции;

- вектор Y = (y₁, y₂, y₃,…,y_n) – вектор цен за единицу каждого вида товара.

Тогда цена всей партии товара найдется как скалярное произведение X∙Y.

Ответ

Цена всей партии товара равна

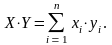
Пример 23 (о количестве сырья, необходимого для выпуска продукции)

Предположим, что некоторое сырье используется для производства n видов продукции так, что для выпуска продукции i-го вида требуется m_i единиц данного сырья. Найти полную потребность q предприятия в сырье в сырье данного вида.

Решение

Сформируем два вектора:

- вектор M = (m₁, m₂, … , m_n) – вектор норм расхода на каждый вид продукции;

- вектор P = (p₁, p₂, … , p_n) – вектор-план выпуска продукции.

Тогда q определится как скалярное произведение M∙P.

Ответ

Полная потребность производства в сырье данного вида определится как