41 Билет

Критерий подобия — безразмерная величина, составленная из размерных физических параметров, определяющих рассматриваемое физическое явление. Равенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие физического подобия этих систем.

В гидромеханике важнейшими критериями подобия являются:

• Число Рейнольдса:

. Определяет, в частности, переход от ламинарного режима к турбулентному.

• Число Маха:

.

• Число Фруда:

В этих примерах

 — плотность жидкости или газа,

 — характерный размер,

 — скорость течения,

 — динамический коэффициент вязкости,

 — кинематический коэффициент вязкости ,

 — местная скорость распространения звука в движущейся среде.

Каждый из критериев подобия имеет определенный физический смысл как величина, пропорциональная отношению однотипных физических величин. Так, число   характеризует отношение инерционных сил при движении жидкости или газа к силам вязкости, а число   — отношение инерционных сил к силам тяжести.

Основными критериями подобия процессов теплопередачи между жидкостью (газом) и обтекаемым телом являются число Прандтля  , число Нуссельта  , число Грасгофа  , а также число Пекле   и число Стэнтона  . Здесь α — коэффициент теплоотдачи^{[источник не указан 381 день]}, λ — коэффициент теплопроводности, c_p — удельная теплоёмкость жидкости или газа при постоянном давлении,   — коэффициент температуропроводности, b — коэффициент объёмного расширения, ΔT — разность температур поверхности тела и жидкости (газа). Два последних числа связаны с предыдущими соотношениями: Ре = Pr×Re, St = Nu/Pe.

теоремы подобия

1 )Подобные явления имеют идентичные соответствующие критерии подобия. Используя эту теорему, можно ответить на вопрос, какие величины следует измерять в опытах,- измерению подлежат те величины, которые входят в состав критериев подобия.

2) Любая зависимость между переменными, описывающими определенное явление, может быть представлена в виде зависимости между критериями подобия (или безразмерными комплексами этих величин): Данная теорема указывает на то, что результаты измерений следует обобщать в виде уравнений, в которых переменными являются критерии подобия. Это существенно сокращает число переменных и, таким образом, упрощает обобщение результатов измерений.

3) Чтобы два явления были подобными, они должны иметь идентичные, так называемые определяющие критерии подобия и подобные условия однозначности. Согласно этой теореме, полученные результаты опытов можно распространить на подобные случаи, для которых определяющие критерии подобия будут идентичными, условия же однозначности будут подобными.

Билет 42

Теплоотдача при свободном ламинарном движении вдоль вертикальной пластины Пусть вертикальная пластина с неизменной температурой поверхности, равной t_c, находится в жидкости или газе. Жидкость вдали от пластины неподвижна (вынужденное течение отсутствует), температура жидкости вдали от пластины постоянна и равна t₀. Для простоты вычисления примем, что t_c>t₀ (однако полученные результаты будут справедливы и для обратного соотношения температур). При этом у пластины появляется подъемное движение нагретого слоя жидкости. Вдали от пластины скорость по-прежнему равна нулю. Расположим начало координат у нижней кромки пластины, а ось Оу нормально к ее поверхности (рис. 10.1). Будем полагать, что пластина вдоль оси Oz бесконечна. Процесс стационарный.

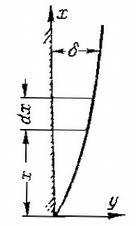
Рис. 10.1. К выводу формулы для коэффициента теплоотдачи при свободной тепловой конвекции

Для упрощения решения задачи примем следующие допущения:

1. силы инерции пренебрежимо малы по сравнению с силами тяжести и вязкости;

2. конвективный перенос теплоты, а также теплопроводность вдоль движущегося слоя жидкости можно не учитывать;

3. градиент давления равен нулю;

4. физические параметры жидкости (исключая плотность) постоянны; плотность является линейной функцией температуры.

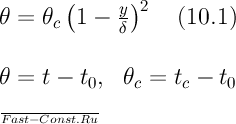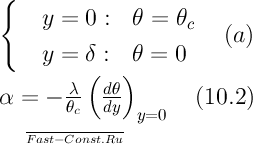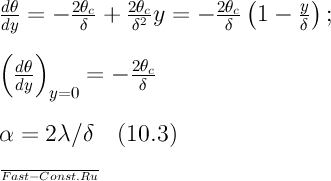Будем полагать, что температура в движущемся слое жидкости изменяется по уравнению согласно условию задачи θ_c=const. Уравнение (10.1) удовлетворяет граничным условиям (a); коэффициент теплоотдачи определяется уравнением (10.2): Из уравнения (10.1) следует, что Подставляя значение (dθ/dy)_y=0 в уравнение теплоотдачи (10.2), получаем выражение (10.3). Толщина движущегося слоя жидкости переменна по высоте и связана со скоростью движения в этом слое. Поле скоростей описывается уравнением движения. При принятых условиях течение происходит в основном в направлении оси Ох, поэтому используем уравнение движения только в проекциях на ось Ох. Для стационарного течения т с учетом ранее принятых допущений уравнение движения упрощается. В результате вместо уравнения (4.18) будем иметь: 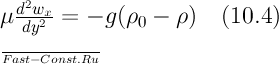При линейной зависимости плотности от температуры 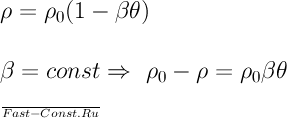Подставляя значение θ согласно (10.1) в уравнение (10.4) и учитывая последнее соотношение для плотности, уравнение движения можно написать следующим образом: 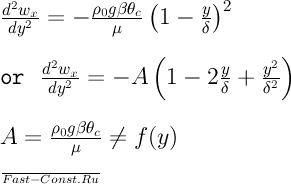Интегрирование уравнения движения даёт Примем следующие граничные условия для скорости: ω_x=0 как при у=0, так и при у=δ. Отметим, что, строго говоря, при y=δ (θ=0) скорость может быть не равна нулю. Это объясняется действием сил вязкости. Движущиеся частицы могут увлекать за собой слои жидкости, находящиеся в изотермических условиях. 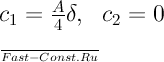При принятых граничных условиях из уравнения (b) следует, что Подставив значения c₁ и с₂ в уравнение (b) и произведя некоторые преобразования, получим следующее уравнение распределения скоростей в движущемся слое жидкости: 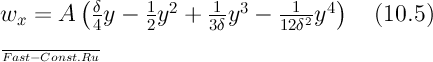На рис. 10.2 приведено распределение скоростей согласно уравнению (10.5). Здесь же представлена кривая температур согласно уравнению (10.1). 

Рис. 10.2. Распределение температуры и скорости согласно уравнениям (10.1) и (10.5)

Максимум скорости соответствует значению Заметим, что распределение скоростей при y=δ не удовлетворяет условию (dω_x/dy)_y=δ=0. Производная при у=δ имеет конечное значение. Это обстоятельство является следствием приближенности решения. Характер изменения скорости на внешней границе движущегося слоя показан пунктирной линией. Согласно уравнению (10.5) среднеинтегральная скорость равна: Для простоты решения среднюю температуру жидкости в слое определим приближенно как среднеинтегральную по сечению слоя (интегрирование согласно формуле (6.1) дает:   что при малых θ_снезначительно отличается от θ_с/3) и получим выражение (10.7). Таким образом, при принятых условиях величина средней температуры слоя не зависит от координаты x. Расход жидкости через поперечное сечение слоя 6·1 равен: Расход жидкости определен по плотности ρ₀. При этом полагаем, что жидкость плотностью ρ₀, вовлекаясь в движущийся слой, приобретает в среднем скорость  . Подставляя в (c) значение  согласно уравнению (10.6), получаем: 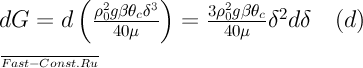В движение вовлекается жидкость с первоначальной температурой t₀. В движущемся слое эта жидкость нагревается до различных температур, лежащих в интервале от t₀ до t_c. Можно считать, что в среднем жидкость нагревается до температуры  . На этот нагрев затрачивается теплота 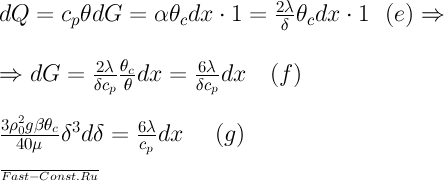Приравнивая правые части уравнений (d) и (f), получаем дифференциальное уравнение, описывающее изменение δ по высоте стенки - выражение (g). Интегрируя это уравнение получаем: 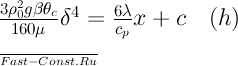Постоянную интегрирования с найдем из условия, что при х=0 δ=0. Отсюда с=0. Из уравнения (h) следует, что 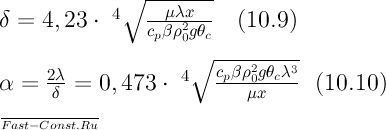Согласно уравнению (10.3)  =2λ/δ. Подставляя сюда значение δ, получаем выражение (10.10). Приведем уравнение (10.10) к безразмерному виду, для чего левую и правую части уравнения умножим на х и разделим на λ. После некоторых преобразований получим: