Первый замечательный предел

Доказательство

Рассмотрим односторонние пределы и и докажем, что они равны 1.

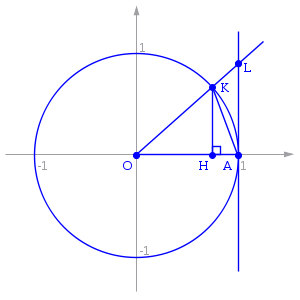
Пусть . Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

(1)

(где S_sectOKA — площадь сектора OKA)

(из : | LA | = tgx)

Подставляя в (1), получим:

Так как при :

Умножаем на sinx:

Перейдём к пределу:

Найдём левый односторонний предел:

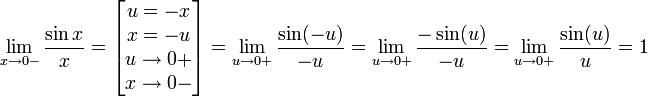
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

Вторым замечательным пределом называется предел

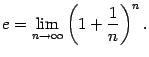
Следствия

1. 

2. 

3. 

4. 

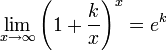
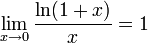
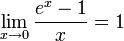
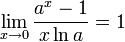5. для ,

6. 

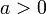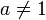
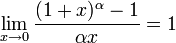
#47

Формула Тейлора

Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Теорема:

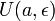
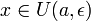
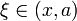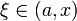Пусть функция f(x) имеет n + 1 производную в некоторой окрестности точки a, Пусть Пусть p — произвольное положительное число, тогда: точка при x < a или при x > a:

#48

Экспонента:

Натуральный логарифм:

для всех

В частности:

• Квадратный корень:

для всех

для всех | x | < 1

Тригонометрические функции:

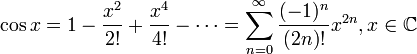
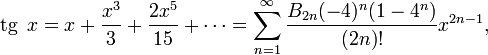для всех где B_2n — Числа Бернулли

для всех

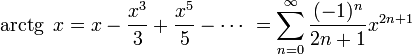для всех

#49

Достаточные признаки возрастания и убывания функции.

На основании достаточных признаков находятся промежутки возрастания и убывания функции. Вот формулировки признаков:

• если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X;

• если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

• найти область определения функции;

• найти производную функции;

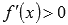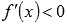• решить неравенства и на области определения;

• к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

Достаточные признаки экстремума функции.

Для нахождения максимумов и минимумов функции можно пользоваться любым из трех достаточных признаков экстремума. Хотя самым распространенным и удобным является первый из них. Первое достаточное условие экстремума. Пусть функция y = f(x) дифференцируема в -окрестности точки , а в самой точке непрерывна. Тогда

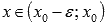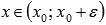• если при и при , то - точка максимума;

• если при и при , то - точка минимума.

Другими словами:

• если в точке функция непрерывна и в ней производная меняет знак с плюса на минус, то - точка максимума;

• если в точке функция непрерывна и в ней производная меняет знак с минуса на плюс, то - точка минимума.

Алгоритм.

• Находим область определения функции.

• Находим производную функции на области определения.

• Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (эти точки называют точками возможного экстремума, проходя через эти точки, производная как раз может изменять свой знак).

• Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).

• Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак.

Второй достаточный признак экстремума функции. Пусть ,

• если 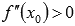, то - точка минимума;

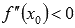• если , то - точка максимума.

Третий достаточный признак экстремума функции. Пусть функция y = f(x) имеет производные до n-ого порядка в -окрестности точки и производные до n+1-ого порядка в самой точке . Пусть и . Тогда,

• если n – четное, то - точка перегиба;

• если n – нечетное, то - точка экстремума.

Причем,

• если 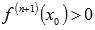, то - точка минимума;

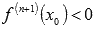• если , то - точка максимума.

Сформулируем теорему, которая позволяет определять промежутки выпуклости функции. Если функция y = f(x) имеет конечную вторую производную на интервале Х и если выполняется неравенство ( ), то график функции имеет выпуклость направленную вниз (вверх) на Х.

Сформулируем необходимое условие перегиба графика функции. Пусть график функции y = f(x) имеет перегиб в точке и имеет при непрерывную вторую производную, тогда выполняется равенство .

Второе достаточное условие перегиба графика функции. Если , а , тогда является абсциссой точки перегиба графика функции y = f(x).