
- •8) Робочі газоподібні тіла поділяються на ідеальні та реальні. Одне й те ж робоче тіло відноситься до ідеального газу чи реального в залежності від термодинамічного ста-ну, в якому воно знаходиться.
- •1000 Молей. Введемо для кіломоля позначення , . Тоді добуток є об’ємом кіломолю газу , .
- •16) Розрізняють також істинні та середні теплоємкості.
- •20) Ізобарний, ізотермічний, ізохорний, адіабатний.
- •25) Поняття колового процесу чи циклу виникло в тд у зв’язку з вивченням процесів,
- •2 Розглянемо довільний прямий оборотний цикл , зображений на рисунку 5.
- •27) Ентропія є шостим параметром стану робочого тіла. Ентропія характеризує напря-
- •3 Введення поняття ентропії дозволяє застосувати для дослідження термодинаміч-них процесів нову (замість введеної раніше - діаграмі) прямокутну систему коор-
- •2 8) Ізохорним називають процес, який протікає при постійному об’ємі, його
- •29) Процес, який протікає при постійному тиску, називають ізобарним. Рівняння
- •30) Процес, який протікає при постійній температурі ( або , нази-
- •31) Адіабатним називається процес, який здійснюється без теплообміну між газом і зовнішнім середовищем. В такому процесі теплота не підводиться і не відводиться,
- •32) Розділення речовини на газ і пару умовне, бо між ними не існує будь - якої межі.
- •33) ) Розглянемо процес перетворення води в пару в Рv- координатах при деякому постійному тиску р. Нехай при даному тиску р 1 кг води з температурою 0 займає об’єм (точка а на рисунку 5).
- •34) Процес пароутворення в Тs – діаграмі
- •Питання 2 Зображення термодинамічних процесів водяної пари в Рv -, Тs - та і,s – діаграмах
- •3 Процеси змішування двох потоків.
- •41) Згідно закону Фур’є вектор щільності теплового потоку пропорційний вектору градієнту температури, але направле-ний в протилежний бік
- •42) Коефіцієнт теплопровідності, його залежність від різних факторів
- •43) Теплопровідність плоскої одношарової стінки
- •44) Теплопровідність багатошарової плоскої стінки
- •46) Теплопровідність циліндричної багатошарової стінки
- •51) Теплопередача крізь плоску стінку
- •52) Температури на зовнішніх поверхнях стінки і на межі двух будь - яких шарів у багатошаро-
- •53) 2 Теплопередача через циліндричну стінку
- •54) Для багатошарової циліндричної стінки відповідні формули мають вигляд
- •55) Особливістю променистого теплообміну є відсутність безпосереднього стикання тіл. Теплообмін може відбуватися при великій відстані від одного тіла до іншого.
- •Випромінювання.
- •57) Закон Планка встановлює зв’язок енергії власного випромі- нювання абсолютно чорного тіла з довжиною хвилі і температурою
16) Розрізняють також істинні та середні теплоємкості.
Істинною
теплоємкістю називається
відношення кількості теплоти
 ,
яка на-дається в елементарному процесі
1 кг газу, до нескінченно малої зміни
температури
,
яка на-дається в елементарному процесі
1 кг газу, до нескінченно малої зміни
температури
 :
:
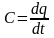 (27)
(27)
Середньою
теплоємкістю
 називається кількість
теплоти, яка в середньому витрачається
в процесі нагрівання 1 кг газу на 1
в інтервалі температур від
називається кількість
теплоти, яка в середньому витрачається
в процесі нагрівання 1 кг газу на 1
в інтервалі температур від
 до
до
 :
:
 (28)
(28)
Кожному певному значенню температури відповідає певне значення теплоєм-кості, яка і є істинною (рисунок 4). А середня теплоємкість в інтервалі температур від до до – це середнє арифметичне між всіма значеннями істинних теплоємкос-
тей, які відповідають кожній температурі з цього інтервалу. Чим менша різниця
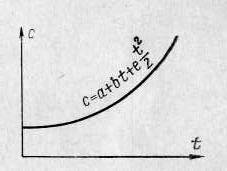 (
( ),
тим більше значення середньої теплоєм-
),
тим більше значення середньої теплоєм-
кості наближається до істинної.
Рисунок 4 - Нелінійна залежність
теплоємкості від температури.
Так вираз середньої масової теплоємкості має вигляд:
 ,
(29)
,
(29)
де
 і
і
 - середні масові нелінійні теплоємкості
від 0
до
і від 0
- середні масові нелінійні теплоємкості
від 0
до
і від 0
до , .
Звичайно
вивчають теплоємкості тільки двох
найбільш важливих процесів нагрі-вання
газів: ізохорного ( )
та ізобарного (
)
та ізобарного ( ).
).
Теплоємкість
газу в ізохорному процесі (
)
називається ізохорною
і по-значається:
 -
масова,
-
масова,
 -
об’ємна,
-
об’ємна,
 -
мольна.
-
мольна.
Теплоємкість
газу в ізобарному процесі (
)
називається ізобарною
і по-значається:
 -
масова,
-
масова,
 -
об’ємна,
-
об’ємна,
 -
мольна.
-
мольна.
Між ізохорними та ізобарними теплоємкостями існують певні співвідношен-ня, які називаються рівняннями Майєру.
При
термодинамічних дослідженнях часто
використовується відношення ізо-барної
теплоємкості до ізохорної. Воно
позначається буквою
 ,
яка називається по-казником адіабати:
,
яка називається по-казником адіабати:
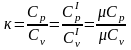 (30)
(30)
Приблизні чисельні значення коефіцієнта складають:
для
одноатомних газів
 ;
для двохатомних
;
для двохатомних
 ;
;
для
трьохатомних
 .
.
Теплоємкості газів змінюються разом із зміною температури, а отже, зміню-ється і коефіцієнт . Так, з рівняння (30) одержують:
 ,
(31)
,
(31)
тобто з підвищенням температури теплоємкість збільшується і, отже, коефіцієнт зменшується.
З рівняння (31) можна отримати вирази для визначення масових ізохорної та ізобарної теплоємкостей
 і
і

17) Закон збереження і перетворення енергії встановлює, що енергія не створюється з нічого і не щезає безслідно, а лише переходить із однієї форми в іншу, від одного тіла до іншого в різних фізичних, хімічних та інших процесах. Перехід енергії одного виду в другий відбувається за зако-ном еквівалентності (пропорційності), тобто певній кількості енергії одного виду завжди відпові-дає одна й та ж кількість енергії другого виду.
Еквівалентність між теплотою і роботою виражається рівняннями
 або
або
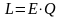 ,
(21,22)
,
(21,22)
де L
– робота, що переходить в теплоту,
 ;
;
Q – теплота, що отримана за рахунок роботи, ккал;
А - коефіцієнт пропорційності, який називають термічним еквівалентом;
Е – механічний еквівалент теплоти.
Значення механічного еквіваленту теплоти приймають рівним
 ,
а термічного
,
а термічного
 .
.
В подальшому для вимірювання теплоти і роботи буде використовуватися одиниця системи СІ - джоуль (1Дж). Крім цього, є ще позасистемна одиниця вимірювання – кілокалорій (1 ккал):
1 ккал = 4,19 кДж.
18) Види внутрішньої енергії
Внутрішня енергія газу є сумою внутрішніх кінетичної і потенційної енергій
U = Uкин + Uпоm. (23)
Внутрішня кінетична енергія залежить від швидкості руху і маси молекул і складається з енергії поступального, обертального руху молекул, а також енергії коливального руху атомів в са-мих молекулах. Ці види енергій залежать тільки від температури і при її рості підвищуються.
Внутрішня потенційна енергія обумовлюється силами взаємодії між молекулами і зале-жить від відстані між ними і, отже, від питомого об’єму газу. Питомий об’єм у свою чергу зале-жить від температури газу і тиску.
Отже, внутрішня енергія реального газу залежить від параметрів стану газу: Р, Т і v.
В ідеальному газі сили взаємодії між молекулами відсутні і тому внутрішня енергія ідеаль-ного газу дорівнює його внутрішній кінетичній енергії і залежить тільки від температури Т.
В кожному стані газ має певний запас внутрішньої енергії, тому сама внутрішня енергія характеризує його стан, тобто є параметром стану робочого тіла. Вона позначається буквою u, в
системі СІ
виміряється в
 .
Користуються також поза
системною одиницею
.
Користуються також поза
системною одиницею
 .
Між ними існує співвідношення 1
=
4,1868
.
Між ними існує співвідношення 1
=
4,1868
 4,19
.
4,19
.
В ТТД визначається
не абсолютне значення внутрішньої
енергії
 ,
а її зміна під час переходу газу з одного
стану в інший -
,
а її зміна під час переходу газу з одного
стану в інший -
 .
Вважається, що внутрішня енергія газу
дорівнює нулю при нормальних умовах,
тобто при t
= 0 о
С і P
= 760 мм
рт. ст.
.
Вважається, що внутрішня енергія газу
дорівнює нулю при нормальних умовах,
тобто при t
= 0 о
С і P
= 760 мм
рт. ст.
Робота розширення
Робота здійснюється тільки при зміні об’єму газу. Якщо відбувається розширення газу, то в цьому випадку робота здійснюється проти зовнішніх сил. При стисненні, навпаки, газ сприймає роботу зовнішніх сил.
Нехай у циліндрі переміщається без тертя невагомий поршень площею F з положення І в положення ІІ. Це переміщення відбувається при розширенні газу з абсолютним тиском Р, котрий знаходиться в циліндрі з лівого боку поршня (рисунок 1).
При переміщенні поршня на нескінченно малу відстань ds 1 кг газу здійснює елементарну роботу, яка дорівнює
 ,
(24)
,
(24)
де
Р – повна сила, яка діє на поршень.
– повна сила, яка діє на поршень.
Через те, що
абсолютний тиск Р
– величина позитивна, то d і dv
за знаком однакові. Якщо
dv
0,
тобто коли газ розширюється, то і d
0,
отже, робота розширення позитивна. Якщо
dv
і dv
за знаком однакові. Якщо
dv
0,
тобто коли газ розширюється, то і d
0,
отже, робота розширення позитивна. Якщо
dv 0,
тобто газ стискується, то
і d
0,
отже, робота стиснення
негативна.
0,
тобто газ стискується, то
і d
0,
отже, робота стиснення
негативна.
Припустимо, що при переміщенні поршня з положення І в положення ІІ питомий об’єм газу збільшився від v1 до v2. Тоді повна робота може бути визначена за формулою
 .
(25)
.
(25)
В Рv – діаграмі робота розширення (стиснення) зображується площею, що обмежується зверху кривою процесу, віссю абсцис знизу і крайніми ординатами (рисунок 2).
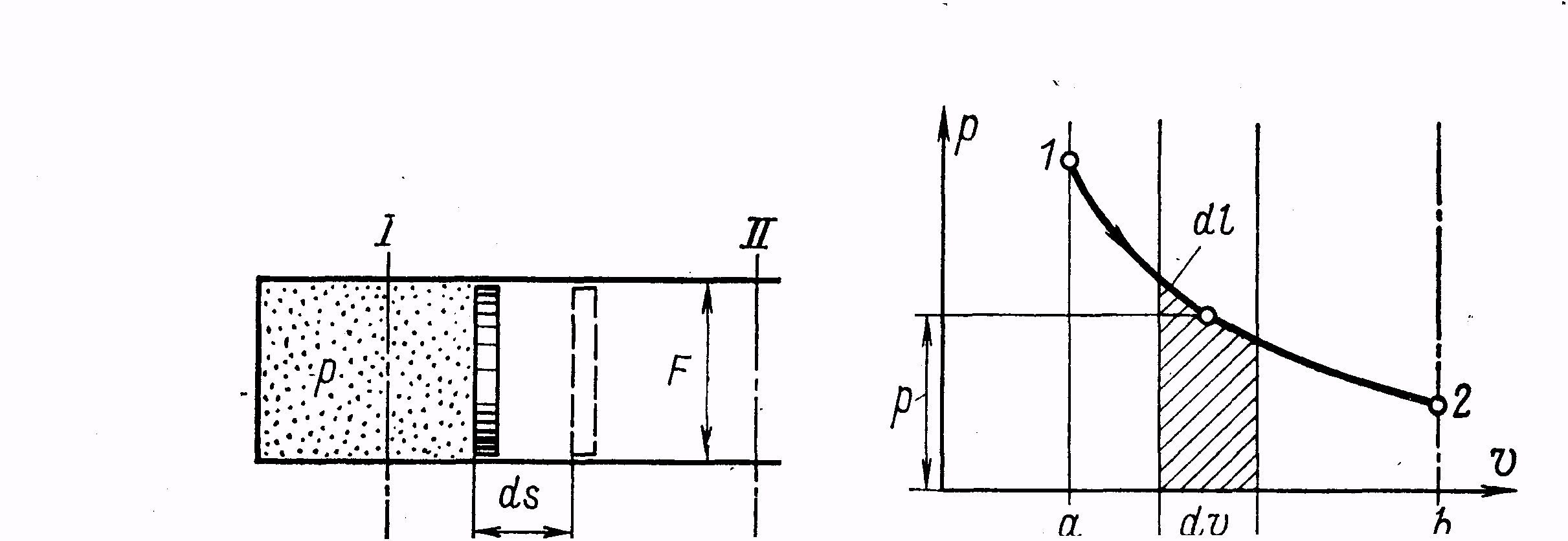
Рисунок 1 - Розширення газу Рисунок 2 - Зображення роботи розширення
в циліндрі газу в Рv – діаграмі
19)
Нехай 1 кг газу здійснює
довільний процес за рахунок теплоти
 ,
яка підводиться ззовні, при цьому
температура та об’єм газу збільшуються.
В результаті підвищення температури й
збільшення об’єму газу його внутрішня
енергія підвищується. Якщо на початку
процесу внутрішня енергія газу дорівнює
,
яка підводиться ззовні, при цьому
температура та об’єм газу збільшуються.
В результаті підвищення температури й
збільшення об’єму газу його внутрішня
енергія підвищується. Якщо на початку
процесу внутрішня енергія газу дорівнює
 ,
а в кінці
,
а в кінці
 ,
тоді повна зміна внутрішньої енергії
дорівнює:
,
тоді повна зміна внутрішньої енергії
дорівнює:
 .
(34)
.
(34)
Крім
цього, збільшення об’єму газу означає,
що він здійснює роботу проти зовнішніх
сил, оскільки газ оточений середовищем,
тобто роботу розширення
 .
.
Якщо в процесі не змінюється зовнішня кінетична енергія газу і в ньому не відбуваються хімічні і будь – які інші зміни, то згідно закону збереження і перетво-рення енергії для процесу, котрий розглядається, баланс енергії виражається рівнянням
 (35)
(35)
Це рівняння є математичним виразом першого закону термодинаміки для кін-цевого процесу. З рівняння (35) витікає, що в загальному випадку теплота, яка підводиться, витрачається на зміну внутрішньої енергії і на здійснення зовнішньої роботи (проти зовнішніх сил).
Отриманий вираз першого закону термодинаміки можна надати в наступному вигляді:
 ,
(36)
,
(36)
або в диференційній формі
 (37)
(37)
Кожна з
величин, котрі входять в рівняння (35) -
(37), може бути позитивною, негативною і
рівною нулю. В ТТД теплота, яка підводиться
до тіла, є позитивною ( ), а та, що відводиться, - негативною (
), а та, що відводиться, - негативною ( ). Зміна внутрішньої енергії вважаєть-ся
позитивною (
). Зміна внутрішньої енергії вважаєть-ся
позитивною ( )
при підвищенні температури газу і
негативною (
)
при підвищенні температури газу і
негативною ( )
при її зменшенні.
)
при її зменшенні.
Ентальпія
У багатьох теплових розрахунках використовується величина, яку називають ентальпією
(або тепловмістом).
Ентальпія – це кількість теплоти, яка
міститься в 1 кг робочого тіла. Вона
по-значається буквою
і та виміряється в
системі СІ в

Ентальпія може бути визначена за формулою
 =
u+R
=
u+R =
=
 +R
=
+R
=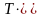 (Cv+R
)=
(Cv+R
)= ,
(26)
,
(26)
де
u
– внутрішня енергія,
 ;
;
Р – абсолютний тиск, Па;
v – питомий об’єм, ;
R
– газова постійна,
 ;
;
Сv і Сp – відповідно масові ізобарна та ізохорна теплоємкості, .
Через те, що u, Р, v – параметри стану робочого тіла, то й ентальпія те ж є параметром ста-ну. З рівняння (26) виходить, що ентальпія - це величина, що визначає стан тіла і залежить від тем-ператури Т для ідеального газу.
Рівняння І закону термодинаміки через ентальпію має вигляд
dq = di
– v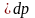 - в диференційній формі
(27)
- в диференційній формі
(27)
або
q
=
 i
– v
i
– v p.
(28)
p.
(28)
