№ вар	Уравнение	x0	y0	h0	a	b
15	y' = y2(2 – x)	0	-1	0.4	0	4

1. Задание для численного решения обыкновенных дифференциальных уравнений:

• дифференциальное уравнение y' = y²(2 – x);

• интервал [0;4];

• начальные условия x₀=0, y₀=-1;

• шаг интегрирования h₀=0.4_.

2. Точное аналитическое решение заданного дифференциального уравнения

Н айдем точное аналитическое решение заданного дифференциального уравнения (решение y=y(x)) методом разделения переменных. Для этого запишем уравнение в виде и проинтегрируем с учетом начальных условий.

Получим . Из начальных условий следует, что с=1.

Аналитическое решение дифференциального уравнения .

3. Значения точного решения ОДУ – y(x)

Вычислим значения полученного решения y(x_i) на отрезке [0;4] с шагом изменения аргумента h=0.4:

4. Численное решение заданного ДУ методом Эйлера

Найдем значения численного решение ОДУ методом Эйлера ( ) в точках отрезка [0;4] с шагом h=0.4. Для этого ДУ записывают в виде y’=f(x,y) . Тогда общая формула для определения очередного значения функции по методу Эйлера имеет вид y_i+1=y_i+h×f(x_i,y_i), где , :

xi
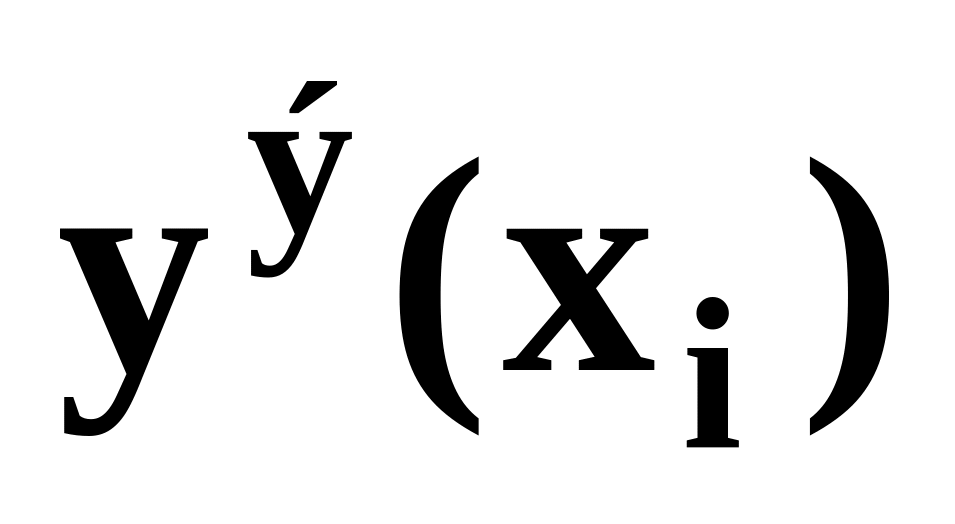
0
0.4	-0.2
0.8	-0.1744
1.2	-0.1598006
1.6	-0.151629
2	-0.1479504
2.4	-0.1479504
2.8	-0.1514527
3.2	-0.1587928
3.6	-0.1708961
4	-0.1895876

5. Значения погрешностей

Вычислим значения погрешностей для , , :

xi	Ei
0
0.4	0.3813953
0.8	0.2641965
1.2	0.2133337
1.6	0.1908368
2	0.1853829
2.4	0.1945154
2.8	0.2216816
3.2	0.2798037
3.6	0.4104992
4	0.8104124

Схема алгоритма и программа решения ОДУ методом Рунге-Кутты 4-го порядка с автоматическим выбором шага

Схема алгоритма

Процедура решения ОДУ в очередной точке

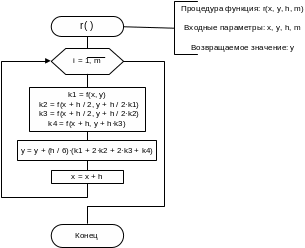
Процедура решения ОДУ методом Рунге-Кутты с автоматическим выбором шага

n=((b - x0) / h0) + 1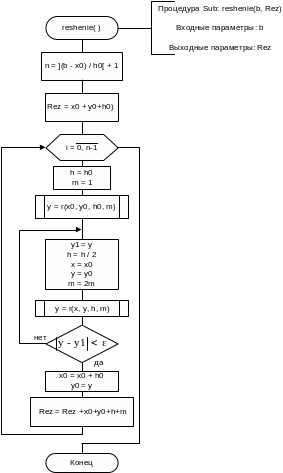

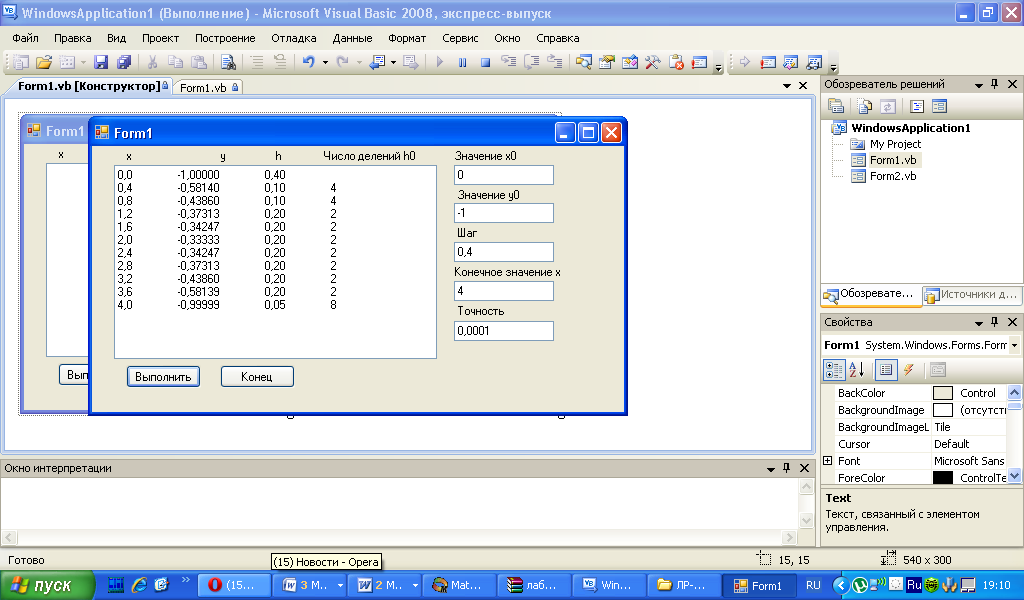
Решение:

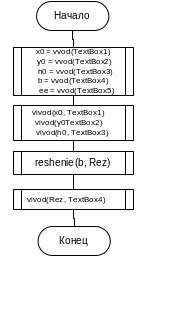
Программный код

Option Explicit On

Imports System.Math

Public Class Form1

Public x0 As Single

Public y0 As Single

Public ee As Single

Public h0 As Single

Public b As Single

'Процедура ввода исходных данных'

Function vvod(ByVal T As TextBox) As Single

Return CSng(T.Text)

End Function

'Описание процедуры функции'

Function f(ByVal x As Single, ByVal y As Single) As Single

Return CSng((y ^ 2) * (2 - x))

End Function

'Процедура вывода результата в TextBox'

Sub vivod(ByVal s As String, ByVal T As TextBox)

T.Text = s

End Sub

'Процедура решения ОДУ в очередной точке'

Function r(ByVal x As Single, ByVal y As Single, ByVal h As Single, ByVal m As Integer) As Single

Dim k1, k2, k3, k4 As Single

Dim i As Integer

For i = 1 To m

k1 = f(x, y)

k2 = f(x + h / 2, y + h / 2 * k1)

k3 = f(x + h / 2, y + h / 2 * k2)

k4 = f(x + h, y + h * k3)

y = y + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4)

x = x + h

Next

Return y

End Function

Sub reshenie(ByVal b As Single, ByRef Rez As String)

Dim n, i, m As Integer

Dim h, y, y1, x As Single

n = CInt(Fix((b - x0) / h0) + 1)

Rez = CStr(FormatNumber(x0, 1)) + Space(15) + CStr(FormatNumber(y0, 5)) + Space(15) + CStr(FormatNumber(h0, 2)) + vbCrLf

For i = 1 To n - 1

h = h0

m = 1

y = r(x0, y0, h0, m)

Do

y1 = y

h = h / 2

x = x0

y = y0

m = 2 * m

y = r(x, y, h, m)

Loop Until Abs(y - y1) < ee

x0 = x0 + h0

y0 = y

Rez = Rez + CStr(FormatNumber(x0, 1)) + Space(15) + CStr(FormatNumber(y0, 5)) + Space(15) + CStr(FormatNumber(h, 2)) + Space(15) + CStr(m) + vbCrLf

Next

End Sub

Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click

Dim Rez As String

Rez = ""

x0 = vvod(TextBox1)

y0 = vvod(TextBox2)

h0 = vvod(TextBox3)

b = vvod(TextBox4)

ee = vvod(TextBox5)

reshenie(b, Rez)

vivod(Rez, TextBox6)

End Sub

Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click

End

End Sub

End Class

Результат выполнения программы