29. Применение закона Био-Савара-Лапласа к расчету магнитного поля возле прямолинейного проводника.

, dlsina=rda; r=b/sina; . Интегрируем от 0 до π. b=r. . Если длина определена, то

30. Применение закона Био-Савара-Лапласа к расчету магнитного поля на оси кругового тока.

В центре. ; Угол между элементом dl и радиус-вектором r равен π/2, поэтому sina=1. Проинтегрируем по dl где l от 0 до 2πR.

На оси. Для нахождения вектора В достаточно сложить проекции векторов dB на ось Z. ; так как угол между dl и r равен π/2, поэтому синус равен 1. Проинтегрируем по окружности, cosβ=R/r, r²= R² + h² . h - расстояние от окружности до точки. .

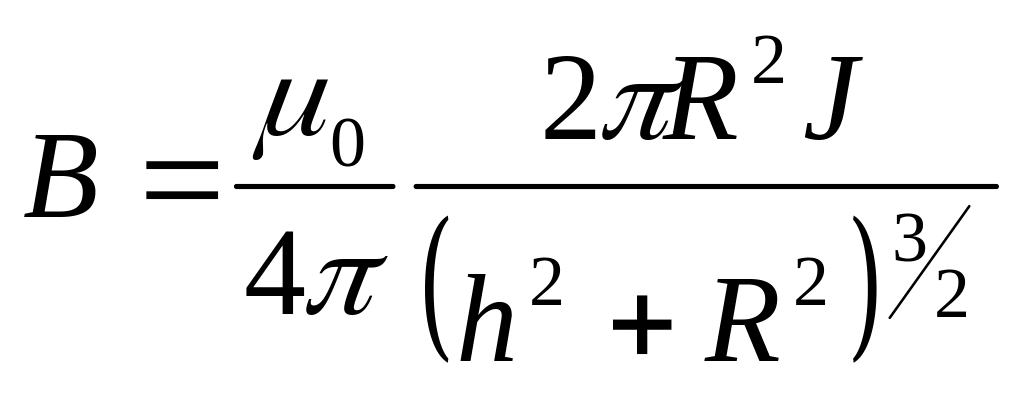32.Сила Лоренца. Движение заряженных частиц в магнитном поле. Принцип действия цилиндрических ускорителей.

На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. ; .

Заряд, движущийся вдоль линии магнитного поля силы не испытывает. Сила Лоренца работы не совершает. Если скорость заряженной частицы перепенд магнитному полю, то под действием силы Лоренца частица будет двигаться по окружности.

В циклотроне заряженная частица, помещенная между полюсами электромагнита, многократно проходит через электрическое поле, каждый раз увеличивая свою энергию на величину от нескольких сотен до нескольких тысяч электронвольт. С увеличением скорости частицы радиус орбиты увеличивается, поэтому частица в циклотроне будет двигаться по спирали.

33. Контур с током в магнитном поле. Момент сил, действующих на рамку с током.

На контур с током в магнитном поле действует сила. На стороны контура не перепенд вектору В силы не действуют. На стороны, перепндикулярные В действует сила F=BIa. Эти силы стремятся повернуть контур, чтобы его плоскость стала ортогональной В. Момент пары сил M=Fh=Flcosα=BIalcosα, где h=lcosα – плечо пары сил.

Величина, численно равная IS (S=al) называется магнитным моментом P_m. P_m=IS. M=B P_m cosα. P_m совпадает с положительным направлением нормали к плокости контура.

33. Циркуляция вектора индукции магнитного поля. Законы полного тока.

Поток вектора В сквозь поверхность S, ограниченную замкнутым контуром, не зависит от формы поверхности S, т.к. линии вектора В нигде не прерываются и их число не зависит от S .

- циркуляция. Вычислим по окружности: Если контур охватывает несколько токов

33. Применение закона полного тока к расчету магнитного поля прямолинейного проводника.

Используем теорему о циркуляции для круглого контура L вне проводника. Тогда B2πr=μ₀I.

Внутри проводника. B2πr=μ₀I_r , где I_r = (r/a)².

33. Применение закона полного тока к расчету магнитного поля тороида.

R- радиус оси тороида. Выделим контур (окружность радиуса r) внутри тороида, он охватывает ток NI. По теореме B2πr=μ₀IN. Отсюда

Вне тороида магнитное поле отсутствует.

33. Магнитный поток. Теорема Гаусса для магнитного поля.

Магн потоком через малую поверхность площадью dS называется скалярная физическая величина, равная , где n – единичный вектор нормали к dS, а Bn – проекция вектора B на нормаль. Магн поток через произвольную замкнутуя поверхность равен . Так как в природе отсутствуют магнитные заряды, поэтому поток вектора В через замкнутую поверхность равен нулю. Таким образом - теорема Гаусса для вектора B (магнитный поток через любую замкнутую поверхность равен нулю)