19. Параметрирование коэффициентов линейной формы

Здесь рассмотрим три варианта параметрирования, отличающихся своими возможностями.

1. Коэффициенты критерия изменяются линейно от параметра:

C()=C+V,

а вектор V задается аналогично случаю изменения ресурсов.

Тогда задача параметрирования имеет вид:

(С+V)^TXmax

AX  B

X  0.

Запишем соответствующую двойственную задачу:

B^TUmin

A^TU  C+V

U  0

Очевидно, что она представляет собой задачу параметрирования вектора ограничений, решение которой может быть получено вышеописанным методом. В результате найдем диапазон изменения параметра  (0   < ), в котором базис двойственной задачи остается неизменным. В строке Z оптимальной таблицы двойственной задачи находятся переменные прямой задачи (двойственные к двойственной). Но значения z_j зависят только от базиса, поэтому в найденном диапазоне  оптимальное решение также не меняется. Изменяться будет только критерий. При достижении критического значения  произойдет смена базиса (оптимальной вершины), а значит, и оптимального решения прямой задачи. Проследить дальнейшее изменение решения можно после повторного решения двойственной задачи с векторм

Т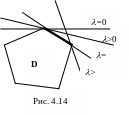 акое поведение следует и из геометрических представлений (рис. 4.14). Изменение коэффициентов линейной формы изменяет наклон линии уровня критерия, но не влияет на допустимое множество. При наличии критических значений  изменение коэффициентов приводит к скачкооб­разному изменению оптимального решения – переходу из вершины в вершину (смежную).

2. Для небазисных переменных весьма просто можно определить диапазон изменения C_j, в котором оптимальное решение остается неизменным.

Действительно, пока при изменения C_j все Δ_j 0 оптимальное решение исходной задачи сохраняет свой статус. Так как

Δ_j = Z_j-C_j,

то уменьшение C_j не может изменить знак оценки. Поэтому интерес представляет увеличение C_j. Пусть + _j, _j .0. Тогда

Δ^’_j = Z_j – C_j - _j = Δ_j - _j  0.

Отсюда следует, что при _j  Δ_j исходное решение остается оптимальным.

3. Этот вариант основан на формуле вычисления относительных оценок в модифицированном симплекс-методе:

.

Она позволяет исследовать влияние изменения любых коэффициентов С_j. В общем случае эти коэффициенты являются некоторыми функциями параметра : C_j(). Тогда условия оптимальности запишутся в виде

Здесь обратная матрица соответствует оптимальному базису. Пока при изменении коэффициентов (т.е. ) эти неравенства выполняются, оптимальное решение не изменяется. Значение , при котором хотя бы одно из условий становится равенством, и будет критическим. Практически оно находится так: каждое условие записывается как равенство и определяются его корни; из всех корней выбирается наименьшее положительное. Это и будет

Очевидно, что данный вариант параметрирования пригоден как для линейных, так и нелинейных зависимостей от параметра. Однако в последнем случае его применение ограничено возможностью нахождения корней нелинейного уравнения.

Пример 4.8. Пусть ожидается изменение коэффициентов критерия в примере 4.2 (разд. 4.9.7) по закону: C₁()=7 - 2, C₂()=5 + . Необходимо определить критическое значение , если таковое имеется.

В оптимальной симплекс-таблице базисные индесы расположены в следующем порядке: 6, 2, 5, 1. Значит, Вычисляем:

Из условий оптимальности Δ₃0, Δ₄ 0 записываем уравнения

Первое уравнение имеет отрицательный корень, корень второго равен 11/8. Таким образом, До этого значения  оптимальное решение не изменяется, при =11/8 имеем альтернативные оптимальные решения (линии уровня L( )=34/8x₁ + 51/8x₂=Const параллельны границе 2x₁ + 3x₂=19), а при >11/8 оптимальное решение переместится в вершину В (рис. 4.3).▲

Как отмечалось выше, параметрические решения могут быть получены также при одновременном изменении правых частей и коэффициентов критерия по линейной зависимости от одного параметра

при линейном изменении столбца условий A_j+V_j или строки a_i+V_i.

В других случаях изменения модели поведение оптимального решения определяется решениями задачи одним из методов ЛП при разных значениях изменяемых параметров модели.