17. Двойственный и модифицированный симплекс-метод Модифицированный алгоритм

Этот алгоритм отличается от рассмотренного в разд. 4.9.6 тем, что основан на обратной матрице базиса. Для простоты расссмотрим случай с односторонними ограничениями на переменные. Тогда небазисные переменные равны нулю, а система условий задачи принимает вид

A_bX_b=B, (4.26)

где A_b – базисная матрица mxm, X_b – вектор базисных переменных. Так как определитель базисной матрицы не равен нулю, существует обратная матрица . Из (4.26) следует, что базисные переменные можно вычислять по формуле

(4.27)

Теперь покажем, что относительные оценки также можно определять по обратной матрице. Для этого выполним ряд преобразований:

(4.28)

Вектор найдем из разложения вектора условий A_j по базису

(4.29)

Подставляя (4.29) в (4.28), получаем

Произведение не зависит от индекса j, поэтому окончательно будем иметь

, (4.30)

где

(4.31)

Таким образом, для решения задачи модифицированным симплекс-методом достаточно вести не всю таблицу, а только обратную матрицу. При единичном начальном базисе обратную матрицу вычислять не надо – она также единичная. Имея обратную матрицу текущего решения, вычисляем сначала вектор по формуле (4.31), а затем оценки небазисных переменных по формуле (4.30). Если признак оптимальности не выполняется, находим минимальную оценку Коэффицинты разложения _ir вектора А_r по текущему базису находятся по формуле (4.29):

где A_r – вектор условий вводимой переменной x_r, который берется из канонической модели. Столбец _r добавляем к обратной матрице в качестве направляющего. Далее действуем, как в стандартном методе, то есть для положительных _ir вычисляем , находим направляющую строку и направляющий элемент. Затем получаем новую обратную матрицу путем симплекс-преобразования теущей обратной матрицы. После выполнения признака оптимальности решение находится по формуле (4.27).

Очевидно, что преимущество этого метода перед стандартным тем выше, чем больше разница между общим числом переменных и числом базисных переменных канонической модели. Однако обнаружение неразрешимости задачи из-за неограниченности критерия может происходить на более поздних итерациях: только тогда, когда соответствующее условие имеет место в направляющем (добавляемом) столбце.

Новую обратную матрицу можно находить не только симплекс преобразованием старой, но и по формуле

,

где E_k – почти единичная матрица (только k-й столбец отличается от единичного). Если эту формулу применять на всех итерациях, то для l-й обратной матрицы получим

.

Такое представление обратной матрицы называют мультипликативным. По сравнению с обычным симплекс-преобразованием оно уменьшает объем вычислений на каждой итерации и тем сильнее, чем меньше плотность матрицы условий.

Учет двусторонних ограничений

В общем случае на переменные могут накладываться двусторонние ограничения _j x_j_j. Каждое такое ограничение порождает 2 равенства в канонической модели и, следовательно, увеличивает размер симплекс-таблицы на 2 строки. Если сместить начало отсчета на _j, ограничение примет вид 0 x_j d_j, где d_j=_j - _j, и таблица будет увеличиваться только на 1 строку. Однако, если такие ограничения накладываются на многие переменные, увеличение размеров симплекс-таблицы будет значительным.

Идея метода с двусторонними ограничениями состоит в учете ограничения сверху аналогично условию x_j 0. Как было показано в разд. 4.9.2, выполнение этого условия обеспечивается выбором направляющей строки, т.е. значения вводимой переменной, равного ₀. Чтобы переменные в новом базисном решении помимо неотрицательности были не больше d_j, усложним выбор значения вводимой переменной. Предельное значение  по условию неотрицательности, вычисляемое по формуле (4.9), обозначим , а предельное значение по ограничению сверху ­– . Из формулы (4.11) следует, что верхнего значения могут достигать только переменные с отрицательными коэффициентами _ir. Приравнивая эти переменные значениям d_j, получаем формулу для вычисления : 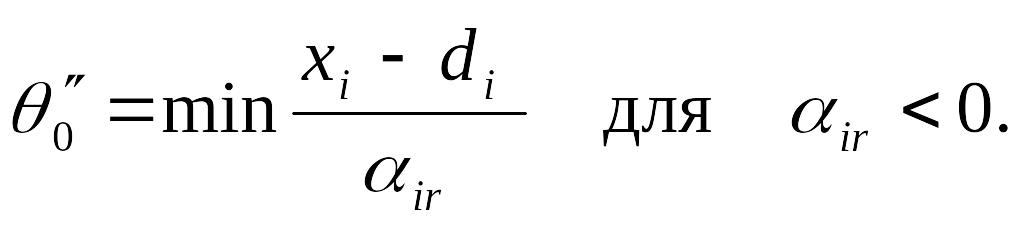(4.24)

Новое базисное решение будет определяться по формуле (4.13), в которой ₀ берется из соотношения

₀=min( ). (4.25)

Соответственно и направляющая строка выбирается по ₀. В симплекс-таблице вместо одного столбца для  удобнее иметь два: для ^’ и ^’’. Кроме того, добавляется одна строка (сверху), в которой записываются значения небазисных переменных: выводимая из базисного решения переменная x_k равна нулю, если в (4.25) < , и равна d_k в противном случае.

Изменяется также признак оптимальности базисного решения. Условие Δ_j0 остается в силе только для нулевых небазисных переменных. К нему добавляется условие для небазисных переменных на верхнем уровне: Δ_j0. Поэтому в случае неоптимальности текущего решения направляющий столбец выбирается по max| Δ_j| из отрицательных для x_k=0 и положительных для x_k=d_k. Симплекс-преобразование (пересчет таблицы) не изменяется.