Метод Хюккеля

Метод МО ЛКАО в варианте Хюккеля был разработан для расчета вполне определенного класса соединений - ненасыщенных углеводородов, обладающих системой сопряженных двойных связей. Несмотря на очевидную грубость использованных приближений, в рамках этого метода удалось уже в 1931 году, задолго до появления первых ЭВМ, описать электронное строение полиенов и сформулировать известное правило Хюккеля.

Специфика строения сопряженных непредельных углеводородов позволяет предположить, что многие их химические свойства определяются электронами π-системы, то есть электронами на орбиталях, антисимметричных относительно плоскости молекулы. Можно строго показать, что электроны связей, расположенных в плоскости молекулы, на вид π МО не влияют, и задача нахождения вида и энергий π МО может быть решена отдельно от описания σ-электронов. В таком случае можно считать, что каждый углеродный атом может быть представлен одной-единственной 2р АО, располагающейся перпендикулярно плоскости молекулы, и исключить из рассмотрения атомы водорода. Это приближение (σ-π-приближение) позволяет сильно упростить задачу. Например, для молекулы бензола в σ-π-приближении достаточно рассмотреть 6 МО, построенных из 6 АО, и разместить на них 6 электронов. Полный же расчет этой молекулы должен включать 36 АО, из которых следует построить 36 МО и заполнить их 42 электронами.

Следующее приближение заключается во введении в теорию двух параметров: параметра α описывающего взаимодействие электрона 2р АО атома углерода со своим ядром, и параметра β характеризующего взаимодействие между двумя соседними атомами углерода, представленными своими 2р АО. Оба эти параметра имеют размерность энергии и отрицательны по величине. Взаимодействием между не связанными непосредственно атомами углерода пренебрегают.

Введенные приближения позволяют свести уравнение Шредингера для молекулы, содержащей n углеродных атомов, к системе n+1 уравнений, неизвестными в которых являются n коэффициентов , квадраты которых определяют вклад АО в МО , и энергия МО . Полная энергия молекулы в приближении Хюккеля определяется как суммарная энергия всех π-электронов, энергия каждого из π-электронов соответствует энергии занимаемой им МО.

Молекула этилена

Рассмотрим применение этого для расчета энергетических характеристик молекулы этилена (риc. 2, а).

В молекуле этилена имеется двенадцать валентных электронов. Из них десять образуют пять σ-связей, т.е. одну связь С-С и четыре связи С-Н. Рассмотрим два π-электрона, которые образуют одну π-связь (риc. 2, б).

Молекулярную орбиталь φ можно представить в виде линейной комбинации двух атомных 2p -орбиталей χ и χ :

φ = c χ + c χ (4)

Коэффициенты с и c можно определить, используя вариационный принцип

= Минимум (5)

где Е — энергия молекулярной орбитали; Н — эффективный одно-электронный гамильтониан. Н, φ и Е относятся к одному π-электрону (одноэлектронное приближение).

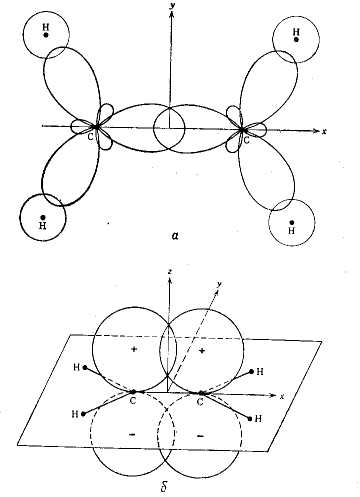
Рис. 2. Изображение σ- и π-связей в молекуле этилена.

Уравнения (4) и (5) по форме совершенно идентичны уравнениям (*) и (**).

(*)

W=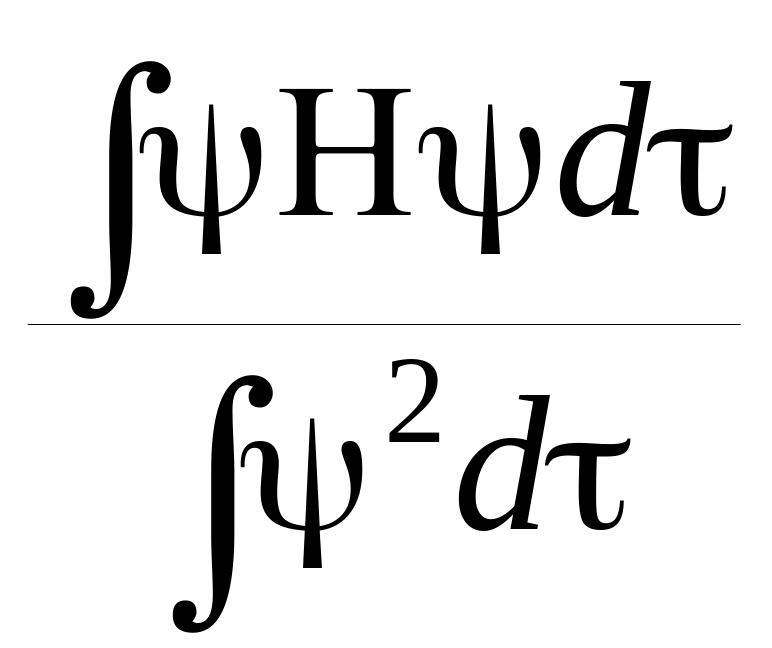 =минимум(**)

(Символы H,W и Ψ, входящие в уравнения относятся не к одному электрону, а ко всей π-электронной системе молекулы).

Вследствие математической идентичности указанных выражений можно записать следующее, полагая, что обе АО нормированы, т. е

(6)

введем следующие обозначения:

Кулоновские интегралы:

(7)

Резонансные интегралы:

(8)

Интеграл перекрывания:

(9)

Кулоновский интеграл , равен энергии одного электрона, принадлежащего атому углерода 1. Эта энергия обусловлена в основном силой притяжения между электроном и ядерным остовом атома углерода 1. При бесконечном удалении электрона от атома углерода эту энергию принимают равной нулю. Таким образом, при конечном расстоянии от атома

<0 и <0

Поскольку оба атома углерода в этилене эквивалентны, разумно предположить, что

(10)

Резонансный, или обменный, интеграл, впервые введенный в квантовой механике, играет очень важную роль в теории химической связи. В отношении знака резонансных интегралов можно предположить, что

<0 и <0

Кроме того, можно показать, что

(11)

Условие (5.8) не ограничивается случаем двух эквивалентных атомов, а является общим соотношением [ср. с уравнением (1 )].

(1 )

Интеграл перекрывания S отражает степень перекрывания двух

атомных орбиталей и , а его величина может находиться в пределах от 0 до 1. Значение S, равное единице, отвечает условию полного совпадения двух АО, т. е. = [уравнение (6)] . Для соседних атомов углерода в молекуле бензола S равен приблизительно 0,25, но при увеличении расстояния между атомами интеграл перекрывания очень быстро уменьшается.

Как мы видели, при соответствующей замене символов уравнение (4) превращается в уравнение (*), а уравнение (5) — в уравнение (**). Сравним теперь условие нормировки (6) с условием (2 ) [ ],а также обозначения уравнений (7) и (8) с уравнением (3 ) [ ; ; ; ] и уравнение (9) с уравнением (2 ). Из сравнения становится ясно, что решение должно дать ряд уравнений, аналогичных уравнениям (4 ) [ ] и (5 ) [ ], а именно:

с ( )+с =0

с +c ( )=0 (12)

Первое равенство (12) получено заменой C ,C H ,H и W в уравнении (4 ) величинами с ,с , , и Е. Аналогично из уравнения (5 ) получают второе равенство (12).

Предположим для простоты, что

S = 0 (13)

В этом случае равенства (12) упрощаются:

c ( )+c =0

c +c ( )=0 (14)

При условии, что коэффициенты с и с не равны нулю, система (14) имеет решение, которое находят с помощью выражения:

=0 (15)

Уравнение (15), называемое вековым уравнением, легко решить:

= 0

или

( )( )=0

Следовательно, это уравнение имеет два корня — и :

(16)

После подстановки значения в уравнение (14) получим

с ( ) + с =0

при

, c =с (17)

Теперь раскроем условие нормировки для МО φ:

или

Каждая АО также нормирована [уравнение (6)], поэтому

(18)

и в предположении, что S = 0,

= 1 (19)

Поскольку ,

=

Молекулярную орбиталь, для которой ,обозначим .Следовательно,

(20)

Для молекулярной орбитали , энергия которой равна , аналогичным путем получают выражение

= (21)

Итак, мы нашли две молекулярные орбитали и , определяемые уравнениями (20) и (21), со значениями энергии и соответственно, которые можно вычислить по уравнению (16).

МО более устойчива, чем МО . Поскольку резонансный интеграл отрицателен, состояние с наинизшей энергией отвечает сумме . Следовательно,

< < = (22)

На рис. 3. схематически изображены МО и . Между функциями и или их квадратами и имеется заметное различие. В точке на середине расстояния между атомами углерода и , равны нулю, т. е. электрон в центре связи отсутствует. Это соответствует утверждению, что не может участвовать в образовании связи. В отличие от для МО характерна высокая электронная плотность в центре связи, так что орбиталь способна к образованию связи. Поэтому часто называют связывающей орбиталью, а - разрыхляющей орбиталью.

Молекула этилена имеет два π-электрона. В основном состоянии молекулы эти электроны должны занимать самую низкую

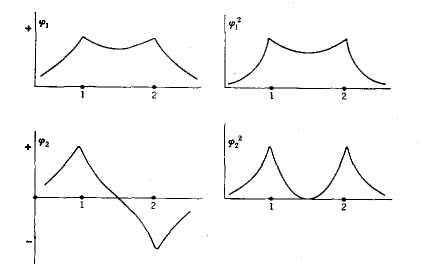
Рис. 3. Молекулярные орбитали и распределение зарядов в молекуле этилена.

по энергии МО . Полная энергия этого состояния равна

W= = 2 (23)

При возбуждении один или два электрона могут промотироваться на МО .Поэтому возможны два состояния с энергиями

W= =

и

W= = (24)

Исходными для этой молекулы являются , и 2р АО углеродных атомов, на каждой из которых расположено по одному электрону с энергией α (в теории Хюккеля нет необходимости использовать численные значения параметров, все энергетические характеристики принято выражать через α и β). В результате расчета (рис. 4) получены две МО: π — связывающая с энергией и π* — разрыхляющая с энергией . Отрицательному знаку при на схеме (рис. 4) соответствует изменение знаков у лепестков p АО на противоположные. В основном состоянии молекулы этилена оба электрона занимают нижнюю МО и π-электронная энергия составляет 2α+2β. Энергия π-связи в этилене, таким образом, равна 2β. Другая экспериментальная характеристика, которая может быть оценена в расчете, — энергия перехода электрона с орбитали на , также равная .

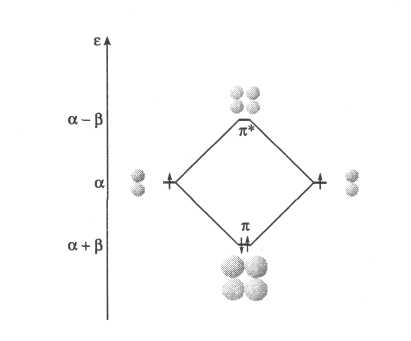
Рис. 4. π-МО в молекуле этилена.