Элементарные операции над частичными функциями:

1. Композиция (подстановка)- ставит в соответствие каждой паре функции f из (N)ⁿ в (N)^m g из (N)ⁿ в (N)^p h = g ° f из (N)^m в (N)^p Которая определяется как D(g ° f) = f^-1 (D(g)) = {x(N)m, D(f) f(x) D(g) f(x) D(g)} (g ° f)(x) = g(f(x))

2. Соединение ставит в соответствие f_i из (N)ⁿⁱ I = 1…K (fⁱ…f^k) из (N)_n в (N)_n1 = (N)_nk

3. h из (N)ⁿ⁺ⁿ в N определяется рекурсией по последнему аргументу.

4. Операция m, которая ставит в соответствие частичную функцию h из (N)ⁿ в N, которая определяется как h(x₁…x_n)=min {X_n+1 f(x₁…x_n)(x+1)=1} Операция m позволяет вводить в вычисление перебор объектов для отыскания нужного в бесконечном семействе.

Теперь, когда определены элементы операции можно дать следующие определения:

1. Последовательность частичных функций f1…fn называют частично-рекурсивным соответствием примитивно-рекурсивным описанием функции f_n = f, если f₁ – одна из простейших функций f_i, для всех i ≥ 2 либо является простейшей функцией, либо получается применением одной из элементарных операций к некоторым из функций f₁…f_n-1 (соответственно одной из элементарных операций кроме n).

2. Функций f называется частично-рекурсивной (соответственно примитивно рекурсивной), если она допускает частично-рекурсивные описания. Теперь можно привести тезис Чёрча в обычной форме. Функция f полувычислима, если, и только если, она частично-вычислима.

3. Функция f вычислима, если, и только если, рекурсивная f и характеристическая функция. (О_о бреееед :D).

Тезис Чёрча может использоваться как определения алгоритмической неразрешимости.

Пусть имеется чёткая последовательность задач P1, P2,…, которые имеют ответ «да» или «нет. Такая последовательность носит название массовой проблемы.

Свяжем с ней функцию f из множества чисел из n в m.

D(f) = {i|P_i имеет ответ да} и f(i) = 1, если i € D(f).

Массовая проблема P называется алгоритмически разрешимой, если функция f и характеристическая функция частично рекурсивны, в противном случае P называется алгоритмически неразрешимой.

Множества.

Мод множеством M понимается совокупность некоторых объектов, которые будут называется элементами множества M. Элементы множества могут сами являться множествами.

Множества можно задать перечислением принадлежащих ему элементов. M = {X₁,X₂,…X_n} или указанием свойств, которым элементы множества должны удовлетворять {X € M| X обладает свойством P}

N – натуральные числа

Z – целые числа

Q – рациональные числа

R – действительные числа

I – иррациональные числа

C – комплексные числа

Операции над множествами:

1 . Объединение множеств (сумма) C= A и B

Множество A и B называются равными, если они состоят из одних и тех же элементов.

2 . Пересечение множеств (произведение) C = A ∩ B

3. Разность множеств. A – B

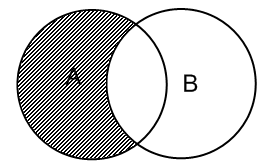
4. Симметричная разность множеств. A\B