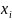5. После того как исходная симплекс-таблица составлена, необходимо выбрать включаемую в базис переменную, исключаемую переменную, а также разрешающий элемент.

Для того чтобы улучшить значение целевой функции переменную, включаемую в базис, необходимо выбирать из условия, если

то s – номер включаемой переменной – номер разрешающего столбца. Таким образом, s – номер столбца с минимальной отрицательной оценкой из оценочной строки.

Исключаемая переменная выбирается по принципу, если

то k – номер исключаемой переменной – номер разрешающей строки. Значит, k – номер строки с минимальным отношением правой части к элементам разрешающего столбца.

На пересечении разрешающей строки и столбца будем иметь разрешающий элемент ( ). В таблице 1.2 выделены разрешающий столбец и строка.

Таблица 1.2 – Исходная симплекс таблица с выделенными разрешающими столбцом, строкой и элементом

			4	5	7	9	0	0	0	0
i		Базис					( )	( )	( )	( )	Решение
1	0		1	3	0	4	1	0	0	0	550
2	0		7	1	3	2	0	1	0	0	350
3	0		5	0	6	5	0	0	1	0	650
4	0		2	4	2	2	0	0	0	1	650
			-4	-5	-7	-9	0	0	0	0	0

6. После того как определены разрешающие элементы исходной симплекс-таблицы, необходимо определить значения всех элементов новой симплекс-таблице соответствующей улучшенному значению целевой функции. Значение новых элементов разрешающей строки определяются делением предыдущих соответствующих значений элементов на разрешающий элемент. Значения остальных элементов новой симплекс таблице определяются по формуле:

Результаты вычислений представлены в таблице 1.3.

Таблица 1.3 – Симплекс-таблица №2

			4	5	7	9	0	0	0	0
i		Базис					( )	( )	( )	( )	Решение
1	0		-3	3	-4,8	0	1	0	-0,8	0	30
2	0		5	1	0,6	0	0	1	-0,4	0	90
3	9		1	0	1,2	1	0	0	0,2	0	130
4	0		0	4	-0,4	0	0	0	-0,4	1	390
			5	-5	3,8	0	0	0	1,8	0	1170

7. Поскольку в индексной строке остались отрицательные оценки, то это приближение не соответствует оптимальному решению задачи. Производим следующие итерации (повторение шагов с 5 по 7) до тех пор, пока в индексной строке остаются отрицательные оценки.

На основании выше сказанного и соответствующих вычислений были получены данные, которые отражены в таблицах 1.3, 1.4 и 1.5.

Таблица 1.3 – Симплекс-таблица №3

			4	5	7	9	0	0	0	0
i		Базис					( )	( )	( )	( )	Решение
1	5		-1	1	-1,6	0	0,33	0	-0,27	0	10
2	0		6	0	2,2	0	-0,33	1	-0,13	0	80
3	9		1	0	1,2	1	0	0	0,2	0	130
4	0		4	0	6	0	1,33	0	0,67	1	350
			0	0	-4,2	0	1,67	0	0,47	0	1320

Таблица 1.4 – Симплекс-таблица №4

			4		5		7		9		0		0		0		0
i		Базис								( )		( )		( )		( )		Решение
1	5		3,36	1		0		0		0,09		0,73		-0,36		0		68,18
2	7		2,73	0		1		0		-0,15		0,45		-0,06		0		36,36
3	9		-2,27	0		0		1		0,18		-0,55		0,27		0		86,36
4	0		-12,36	0		0		0		-0,42		-2,73		1,03		1		131,82
			11,45	0		0		0		1,03		1,91		0,21		0		1372,73

8. Поскольку в последней строке таблицы 1.4 нет отрицательных значений оценки, то она будет соответствовать оптимальному решению данной задачи оптимизации производства. Поскольку оптимальное решение имеет вид:

а в таблице 1.4 присутствуют только аргументы , , , , то решение в нашем случае будет иметь вид:

9. Проверим правильность расчетов. Правильность расчетов проверяется по формуле

Расчет подтверждает правильность сделанных вычислений.

Решение к заданию 2

1. Для определения коэффициентов необходимо определить значения следующих выражений для каждого опыта: 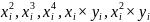. Результаты вычислений были сведены в таблице 2.

Таблица 2 – Результаты вычислений

i
1	87,5	7656,25	669921,9	58618164	292	25550	2235625
2	84	7056	592704	49787136	283	23772	1996848
3	77,8	6052,84	470911	36636872	270	21006	1634267
4	63,7	4057,69	258474,9	16464848	235	14969,5	953557,2
5	46,7	2180,89	101847,6	4756281,2	197	9199,9	429635,3
6	36,9	1361,61	50243,41	1853981,8	181	6678,9	246451,4
∑	396,6	28365,28	2144103	168117283	1458	101176,3	7496384

2. На основании рассчитанных данных (таблица 2) была построена система уравнений. Система уравнений имеет следующий общий вид:

С учетом данных представленных в таблице 2 система уравнений примет вид:

3. Решив данную систему уравнений, получим значения искомых коэффициентов . Так искомые коэффициенты имеют следующие значения:

а₀ = 7,425×10^-3;

а₁ = 1,304;

а₂ = 121,691.

4. После того как значения коэффициентов определены, искомая зависимость примет вид:

На рисунке 1 представлен график, на котором построены экспериментальные данные и аппроксимирующая функция.

Рисунок 1 – График функции (x)

Решение к заданию 3

1. Для перевода натуральных переменных в кодовые значения необходимо знать нулевые уровни, интервалы варьирования, нижние и верхние уровни, для каждой переменной. На основании исходных данных была составлена таблица 3.1 содержащая все необходимые данные.

Таблица 3.1 – Таблица кодирования переменных на двух уровнях

Интервал варьирования и уровень факторов	Скорость резания, м/с	Подача, мм/об	Глубина резания, мм
Нулевой уровень	80	0,3	4,5
Интервал варьирования	10	0,09	0,5
Нижний уровень	70	0,21	4
Верхний уровень	90	0,39	5
Кодовое обозначение

2. Составим план матрицу эксперимента. Отметим, что при составлении план матрицы эксперимента для уровни чередуются в каждом опыте, для – через два опыта, для – через четыре и так далее. В таблице 3.2 представлена план матрица данного эксперимента.

Таблица 3.2 – План матрица эксперимента

Опыт
1	-1	-1	-1	1	1	1	-1	981,7	986	983,85
2	1	-1	-1	-1	-1	1	1	930	912	921
3	-1	1	-1	-1	1	-1	1	673,3	654,2	663,75
4	1	1	-1	1	-1	-1	-1	876	878,7	877,4
5	-1	-1	1	1	-1	-1	1	826,7	881,8	854,25
6	1	-1	1	-1	1	-1	-1	842,7	981,2	911,95
7	-1	1	1	-1	-1	1	-1	775	757,8	766,4
8	1	1	1	1	1	1	1	1005	1006,7	1005,85

Отметим, что количество независимых управляемых факторов (n) в данном эксперименте равно 3, число всевозможных неповторяющихся комбинаций уровней независимых управляемых факторов (N) равно 8.

3. Проверка однородности оценки дисперсии (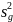 ). В данном эксперименте выполняли по два опыта на одинаковых параметрах, поэтому значение оценки дисперсии в каждой точке плана можно определить по формуле

где – разность между параллельными опытами.

В соответствии с вышесказанным и данными представленными в таблице 3.2 получим следующие значения оценки дисперсии для каждого эксперимента

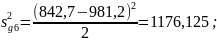
Для проверки гипотезы об однородности оценок дисперсии следует пользоваться критерием Кохрэна (G), который основан на законе распределения отношения максимальной оценки дисперсии к сумме всех сравниваемых оценок дисперсий. Следовательно, значение критерия Кохрэна можно определить по формуле

С учетом выше рассчитанных данных критерий Кохрэна имеет в данном случае следующее значение

Для воспроизводимости процесса необходимо выполнение следующего неравенства

где – критическое значение критерия Кохрэма.

Критически значение критерия Кохрэма является табличным значением и зависит от количества опытов и числа степеней свободы. Количество опытов в каждом эксперименте (m) равно двум, число степеней свободы можно определить по формулам

С учетом имеющихся данных . Для данных условий значение критического коэффициента Кохрэма в соответствии со справочными данными принимаем равным 0,6789.

Как видно из выше представленных данных данный процесс воспроизводим (0,474 0,6789).

4. Определение ошибки опыта. Поскольку процесс воспроизводим необходимо определить ошибку опыта или дисперсию воспроизводимости, которая может быть определена по формуле

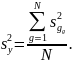
5. Расчет коэффициентов регрессии. После того как подтверждена воспроизводимость процесса необходимо определить коэффициенты регрессии. Расчет коэффициентов регрессии ведется по формулам

В соответствие с выше представленными данными и формулами коэффициенты регрессии примут следующие значения:

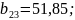
6. Оценка значимости коэффициентов регрессии. Оценка значимости коэффициентов регрессии производится с помощью критерия Стьюдента ( ). Коэффициент считается значимым, если выполняется неравенство

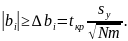
Критическое значение коэффициента Стьюдента зависит от , которое определяется по формуле

В соответствие со справочной литературой при , , тогда 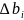равно

Исходя из выше сказанного получаем, что значимым являются коэффициенты регрессии , незначимыми коэффициенты – .

Зная значения значимых коэффициентов регрессии можно составить функцию отклика. В данном случае функция отклика будет иметь вид

7. Проверка адекватности линейной модели. Для проверки адекватности линейной модели пользуются критерием Фшера (F), который определяетя по формуле

где – дисперсия адекватности.

Дисперсия адекватности определяется по формуле

где k – коэффициент равный 3;

– значения полученные путем подстановки соответствующих данных в полученную функцию отклика.

Для упрощения расчетов была составлена таблица 3.3, в которой приведены средние значения откликов, полученных экспериментальным путем, а так же полученных на основании расчетов по составленной функции отклика.

Таблица 3.3 – Сравнение экспериментальных и расчетных данных

Опыт
1	983,85	938,574	0,076
2	921	933,15	147,623
3	663,75	675,9	147,622
4	877,4	877,076	0,075
5	854,25	854,524	0,075
6	911,95	854,8	147,623
7	766,4	754,8	147,622
8	1005,85	1006	0,076

С учетом данных представленных в таблице 3.3 дисперсия адекватности будет равна

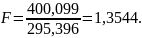
Линейная модель будет адекватна в случае выполнения неравенства

где 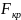– критическое значение критерия Фишера.

Критическое значение критерия Фишера является табличным значение и определяется в зависимости от числа значимых коэффициентов (d) и степеней свободы , которые определяются по формулам

При данных условия и в соответствии со справочной литературой критическое значение критерия Фишера в нашем случае равно 4,07.

Как показывают выше приведенные вычисления составленная линейная модель адекватна (1,3544 4,07).