Автоматизация геометрического проектирования
Для представления объекта новой степени сложности.
Типы математических моделей геометрических объектов:
Структурные математические модели – модели представляются графами, вершины отражают элементы объекта (отдельные геометрические фигуры, точки), дуги – отображают связь между объектами. Если дугам присваивается вес, то такие модели отображают параметрические свойства объекта.
Рецепторные модели. Геометрический объект отображается в пространстве рецепторов.
При сечении пространства плоскостями, перпендикулярными плоскостными координатами, образуется пространственная сетка, каждый элемент которой является рецептором. Рецептору может присваиваться 2 значения.
1 – если этот рецептор содержит элемент объекта
0 – если не содержит.
Рецепторная модель для двухмерного случая.
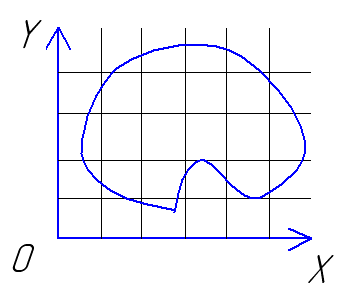
На основании результатов пересечения строится рецепторная модель в виде матрицы.
После составления матрицы определяются координаты каждого дискрета и составляется матрица координат с которой проводятся все дальнейшие преобразования. Точность рецепторной модели зависит от величины дискрета.
Аналитическая модель – наиболее компактная модель, которая задается в виде уравнений и неравенств, но аналитические модели отображают небольшое количество объектов.
Аналитические модели бывают 2 видов:
–уравнения могут быть записаны в явном виде и не в явном.
Y=f(x) – уравнения в явном виде
-уравнения прямой, параллельной оси х: х=а
Неудобна,
т.к.
Тогда
получаем функцию: f(x,y)=0;
,
x-a=0
Аналитическо-логические модели. Могут отображать широкий класс сложных объектов.
В логико-аналитической модели части объекта отображаются аналитическими выражениями. Между собой составные части объекта соединяются с помощью логической функции: пересечение логических функций (u), объединение логических функций (или) и вычитание одного объекта из другого (не).
Пример: f1
– окружность с единичным радиусом в
центре начальных координат f1:
x2+y2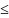
1
f2
– полуокружность уравнения записываются
y>=0.5. Результирующая
фигура f3: f1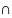
f2
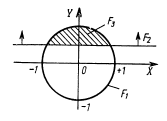
П
ример
2
Цилиндр шар
В результате получили:
U
функции
функция
f2-f1
f2-f1
Каркасные модели
2 вида каркасных моделей:
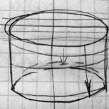
Основан на понятиях образующей и направляющей.
Образующая – в плоскости задаются аналитическим методом. При непрерывном перемещении образующей по заданной траектории, которая определяется направляющими через заданный шаг фиксируются точки пересечения направляющих их и образующих и составляется матрица координат точек пересечения, в которой производятся геометрические преобразования.
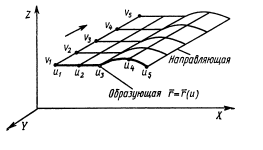V1-V5
– направляющие, U1-U5 -
образующие
Построен на понятии определителя в которое входят две составляющие геометрическая и алгоритмическая. Геометрическая составляющая определяет исходную форму объекта.
Алгоритмическая – определяет правило перемещения объекта.
Каркасная модель получается путем пересечения точек, которые принадлежат исходному объекту при перемещении его с заданным шагом и плоскостей перпендикулярных относительно наблюдателя.
