Билет 4. 1) Виды управления динамическими системами: детерминированное и управление с учетом стохастических факторов.

Нас будет интересовать управление системами, обладающими поведением. Под системой будем понимать совокупность элементов, находящихся в связях (причинно-следственных отношениях) и мыслимых как некоторое единое целое. Природа элементов может быть произвольна. Систему будем характеризовать своим состоянием в момент времени t [0, T], которое будем описывать набором числовых величин-переменных состояния зависящих от времени. Собственно под поведением и будем понимать изменение со временем этих величин.

Обозначим через y(t) – состояние системы в момент времени t. Если переменные состояния – действительные числа и их всего n, то . Таким образом исключаем из нашего рассмотрения так называемые «распределенные» системы, где состояние системы зависит от t и от точки пространства. Отображение описывает эволюцию, движение, поведение системы. Будем предполагать, что эволюция системы описывается некоторой моделью. Здесь возможны самые разнообразные ситуации. Модели могут быть детерминированными, со случайными факторами, с запаздыванием и т.п. Функция в свою очередь может быть непрерывной – разрывной, регулярной (дифференцируемой) – нерегулярной (недифференцируемой) и т. д. Мы ограничимся только детерминированным и стохастическим случаями без запаздывания, приводящими к непрерывной функции состояния системы состояния системы y(t). В детерминированном случае модель чаще всего такова, что y(t) есть решение задачи для дифференциального уравнения с начальными данными: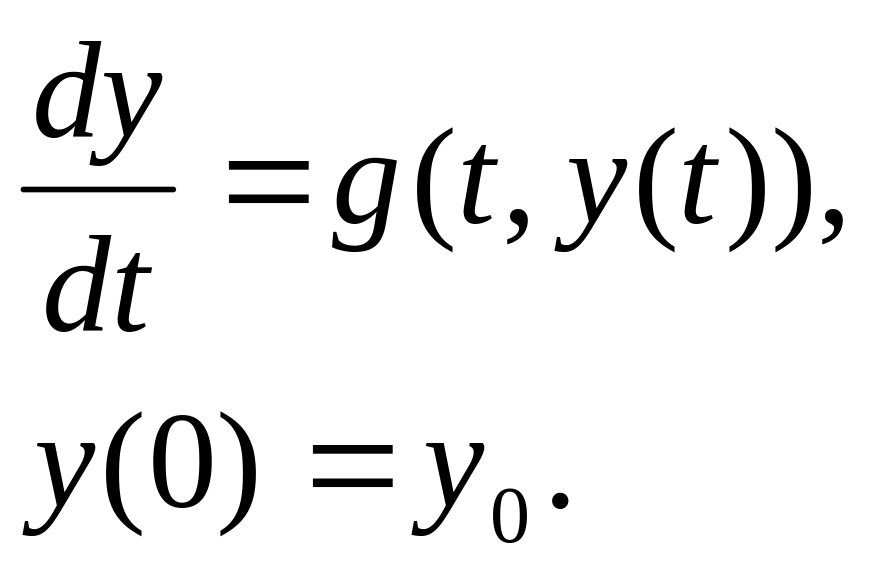 (1)

Пример 1. Система чашка кофе описывается моделью

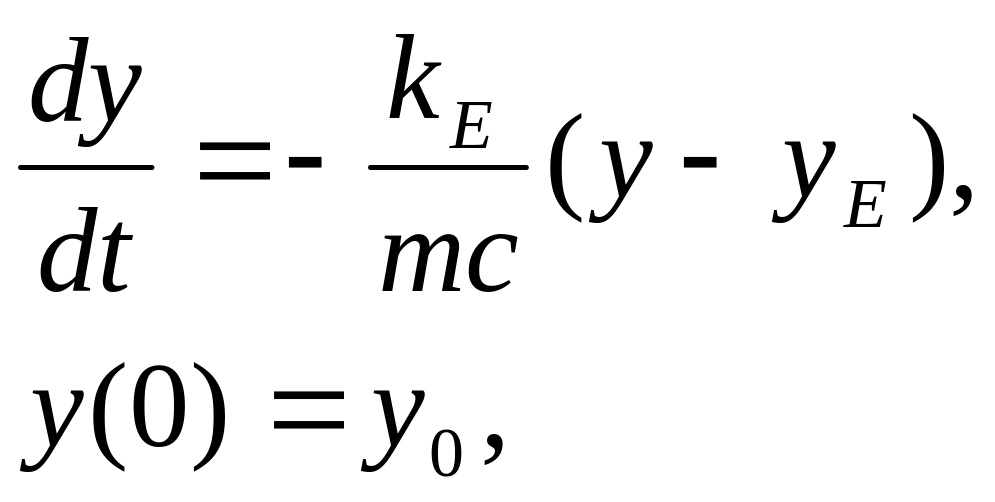где y = y(t) – «средняя» температура системы, y₀ – начальная температура, y_E – температура окружающего чашку воздуха, принимаемой постоянной за время остывания кофе, k_E – коэффициент теплоотдачи, m – масса и с – удельная теплоемкость чашки кофе.

Пример 2. Народонаселение земного шара может быть описано с точки зрения динамики ее численности моделью

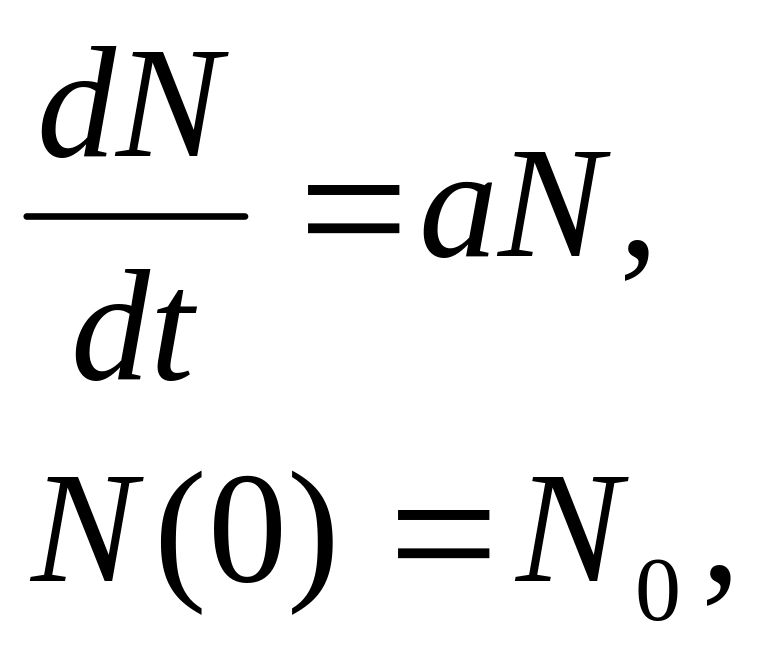где N = N(t) – общая численность, a – коэффициент воспроизводства, N₀ – начальная численность населения Земли.

В общем случае, когда аналитического решения нет или мы не в состоянии его определить, то (1) практически отражает факт изменения состояния системы между t и , где - малый интервал между наблюдениями, как

(2)

где y(t) – состояние системы в текущий момент времени t. Так что состояние системы в момент времени описывается как

(3)

Состояние (3) тем точнее, чем меньше . Такое свойство модели – способность описывать состояние системы в будущем будем называть прогностической функцией модели. С состоянием (3) может быть связана и другая функция модели – объяснительная. При изучении системы мы можем высказать ряд гипотез и построить на их основе модель функционирования системы. Если она достаточно точно описывает наблюдаемое поведение системы, то мы можем с определенной уверенностью утверждать о справедливости высказанных гипотез. Если нет, то вернуться к высказанным гипотезам и подвергнуть их соответствующей модификации.

Если при моделировании мы решили учитывать и случайные факторы, то изменение состояния системы будет уже случайной величиной. В этом случае естественно предположить, что к правой части (2) добавляются случайные поправки. При отсутствии информации о характеристиках случайных процессов (средние, дисперсия, закон распределения) проще всего предположить, что эта случайная поправка распределена по нормальному закону со средним значением равным нулю и дисперсией, зависящей, в общем, и от y(t). Тогда, если две поправки, соответствующие двум не пересекающим интервалам времени независимы, в общем случае можно принять модель (4)

где - матрица, а распределено по нормальному закону со средним О и дисперсией (E – единичная матрица). Соотношение (4) представляет эволюцию системы в виде суммы двух процессов: детерминированного и случайного. Последний может представляться как описание воздействия на систему со стороны окружающей среды.

Важным моментом представления (4) является требование того, что для непересекающихся интервалов времени и были независимы. Это означает, что мы требуем, чтобы случайный процесс был Марковским, независимым от прошлого. Будущее системы будет определяться только его настоящим, так как мы решили процесс запаздывания не рассматривать. В этом случае достаточно предположить, что w(t) есть так называемый n-мерный Винеровский процесс и

(5)

Тогда требуемое свойство независимости от прошлого выполняется. Если , то в общем случае (4) можно записать в виде равенства дифференциалов

(6)

а не в форме производных (1), ибо винеровский процесс, будучи непрерывным и имеющим ограниченную вариацию, не является дифференцируемым. Примером винеровского процесса является, например процесс броуновского движения частиц. Он находит широкое применение при анализе будущих изменений цен активов в финансовых задачах. Именно по этой причине он здесь и упоминается. Уравнение (6) называется стохастическим дифференциальным уравнением. Решение уравнения (6) – непрерывный Марковский процесс, называемый диффузным процессом с приращением процесса g и матрицей - называемой диффузным членом. Если матрица невырождена, т. е. , Е – единичная матрица, а неравенство понимается в смысле для любого вектора , то dy(t), а значит и y(t), может принимать любые значения из Rⁿ с отличной от нуля вероятностью в силу того свойства закона нормального распределения. Это может вносить неудобства при описании содержательных ситуаций в ряде предметных областей, где на y(t) накладываются смысловые (содержательные) ограничения.