
- •Часть 3. Динамика
- •Лекция 1 введение в курс динамики материальной точки и механической системы
- •1.1. Материальная точка
- •1.2. В каком смысле масса есть мера инертности?
- •1.3. Аксиомы классической динамики материальной точки
- •Первая или прямая задача
- •Вторая или обратная задача динамики
- •2.2. Алгоритм решения задач динамики точки
- •2.3. Примеры решения задач динамики точки
- •1. Основная задача внешней баллистики
- •2. Задача о коническом маятнике
- •3. Задача о динамическом давлении транспортного средства типа «трамвай» на рельсы (Как создавать образ математической модели) (рис. 2.3, 2.4)
- •Лекция 3 Динамика относительного движения точки
- •Теорема сложения скоростей
- •Теорема Кориолиса сложения ускорений
- •1. Об Эйлеровых силах инерции
- •2. Условия инерциальности системы координат
- •3. Условия относительного покоя
- •Лекция 4 примеры решения задач
- •1. Уклонение линии отвеса от направления на центр Земли Зависимость ускорения свободного падения от широты места
- •2. Отклонение падающих тел к востоку
- •3. Задача о размыве берегов рек
- •Лекция 5 примеры решения задач (продолжение) Задача о неинерциальном движении шарика вдоль трубки при ее вращении с постоянной .
- •Возможны три случая движения шарика вдоль трубки
- •Рассмотрим вариант зависания шарика
- •Рассмотрим 3-й вариант: решения задачи
- •Лекция 6
- •6.1. Введение в динамику системы. Масса механической системы
- •6.2. Способы определения положения центра масс системы
- •Частные случаи определения цм
- •1 . Метод симметрии (рис. 6.3)
- •2. Метод разбиения на тела (рис. 6.4)
- •3. Метод отрицательных масс (рис. 6.5)
- •Лекция 7
- •7.1. Введение в динамику систем постоянного состава
- •7.1.1. Свойства внутренних сил системы
- •7.1.2. Уравнения движения системы в форме Ньютона-Эйлера
- •7.2. Общие теоремы динамики системы
- •(2)Теорема о движении центра масс системы
- •(3) Теорема об изменении кинетического момента системы
- •Когда и где применяется эта теорема?
- •Лекция 8
- •8.1. Вычисления кинетической энергии системы
- •8.2. Кинетическая энергия тела при простейших его движениях
- •3. Плоское движение твердого тела
- •4. Сферическое движение твердого тела
- •5. Произвольное движение твердого тела.
- •Пример 2. Работа силы тяжести
- •9.4. Мощность и работа реакций идеальных связей
- •9.5. Мощность и работа диссипативных сил и пар сил как реакций неидеальных связей
- •Лекция 10
- •10.2. Радиус инерции
- •Что есть радиус инерции?
- •Лекция 11
- •11.1. Теоремы о движении центра масс системы и об изменении количества движений системы
10.2. Радиус инерции
В данной задаче i2 есть радиус инерции составного второго тела.
Что есть радиус инерции?
С
точки зрения физических
основ механики,
во-первых,
радиус инерции ТТ
(i)
равен
приведенной длине
 эквивалентного
математического маятника той же
массы
и того же
момента инерции составного тела
относительно оси вращения
эквивалентного
математического маятника той же
массы
и того же
момента инерции составного тела
относительно оси вращения
 .
.
Или,
во-вторых, радиус
инерции
равен
приведенному радиусу тонкого
обруча,
имеющего ту же массу и тот же момент
инерции относительно оси вращения.
Здесь
 .
.
Вычислим моменты инерции тел 2 и 3, входящих в систему:
 .
.
Скомпонуем выражение кинетической энергии системы.
В прикладной механике активно используется прием, когда исходная система с S=1 приводится по кинетической энергии к эквивалентной (приведенной) массе mпр, движущейся с искомой скоростью v и ускорением a, или эквивалентному диску с приведенным моментом инерции. Покажем это:


 ,
,

Таким
образом,
для системы с одной степенью свободы
структура выражения кинетической
энергии принимает вид:
 ,
вне
зависимости от структурной сложности
рассматриваемой системы.
,
вне
зависимости от структурной сложности
рассматриваемой системы.
7.
Вычислим левую часть теоремы: .
.
8. Вычислим суммарную мощность в правой части теоремы. Заметим, что мощность и работа идеальных связей равны нулю. Поэтому такие силы и пары сил можно не изображать на расчетной схеме. Тогда


 ,
,
 ,
,

Заметим,
что для систем с S
= 1 структура
выражения мощности
при постоянных силах всегда
будет иметь вид
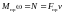
9.
Скомпонуем теорему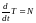 :
:

 .
.
10. Найдем решение задачи:


 ,
,
возьмем
 ,
получим
,
получим
 .
.
2-я часть задачи
Получим ответ на поставленный во второй части вопрос, привлекая выкладки предыдущей задачи:
1)
 ;
;
2)

 .
.
Вывод
Для любых по структуре систем с одной степенью свободы при постоянных силах и парах сил, действующих на нее, задачи такого типа являются типовыми с одинаковыми по структуре ответами.
Лекция 11
11.1. Теоремы о движении центра масс системы и об изменении количества движений системы
Рассмотрим движение системы как целого, в котором можно выделить некоторую поступательную часть ее движения. Тогда, чтобы отбросить вращательную часть движения системы, достаточно просуммировать уравнения Ньютона–Эйлера по точкам.
 ,
,
Быстрота изменения количества движения системы равна главному вектору только внешних сил.
Из этого вытекают три следствия.
Следствие 1
Только внутренние силы непосредственно не могут изменить количество движения системы. В классической механике невозможно самовозбуждение движения под действием только внутренних сил. Однако опосредованно можно: через возбуждение внешних диссипативных сил. Например, сил кулоновского, вязкого, магнитного и других видов трения.
Следствие 2
Если
 ,
то
,
то

Если главный вектор внешних сил равен нулю для всех t, то количество движения сохраняется и имеет место “закон сохранения количества движения системы”.
В математике в этом случае говорят: имеет место первый интеграл уравнений движения – интеграл импульсов.
Следствие 3
Если
 ,
то
,
то

Количество движения (импульс) по выделенному направлению при этом условии сохраняется.
Вывод теоремы о движении центра масс.
 так
как
так
как
 ,
то
,
то
 .
.
Если
,
то
 .
.
Если
,
то

