3.1. Краткие сведения из теории

Частотные характеристики систем (звеньев) заключают в себе полную информацию о динамических свойствах так же, как и диффе­ренциальные уравнения и передаточные функции, которыми они опи­сываются.

Частотные характеристики вытекают из комплексного коэффициента усиления системы (звена), который может быть представлен в виде:

, (3.1)

где – модуль комплексного коэффициента усиления;

– аргумент комплексного коэффициента усиления;

и – действительная и мнимая части комплексного ко­эффициента усиления соответственно.

Изменение модуля и аргумента комплексного коэффициента усиления в функции частоты , представленное в виде годографа на комплексной плоскости, называют амплитудно-фазовой характеристикой (рис. 3.1 ).

Модуль и аргумент комплексного коэффициента усиления как функции частоты представляют собой две частотные характерис­тики – амплитудно-частотная и фазочастотная.

Действительная и мнимая части комплексного коэффициента усиления представляют собой вещественную и мнимую частотные характеристики.

К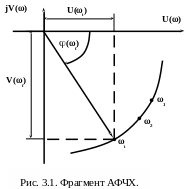 аждая из этих характеристик может быть определена через дру­гие частотные характеристики

;

; (3.2)

;

.

Одним из достоинств применения частотных характеристик является возможность их экспериментального получения. Эксперимент заключается в следующем. На вход системы (звена) подается синусоидальный сигнал

,

а на выходе системы (звена) измеряются параметры выходного сину­соидального сигнала – амплитуда и его фазовый сдвиг по отношению к входному сигналу. Причем, частота входного сигнала изменяется в ходе измерений от нуля до бесконечности (теоретически).

Для каждого значения частоты подсчитываются значения комплекс­ного коэффициента усиления и, в дальнейшем, по полученным данным строятся частотные характеристики.

В данной работе для апериодического, реального дифференцирующего и колебательного звеньев определяются частотные характеристики: комплексный коэффициент усиления (амплитудно-фазовая частотная характеристика звена); вещественная и мнимая частотные характеристики; амплитудная и фазовая частотные характеристики; логарифмические амплитудная и фазовая частотные характеристики.

При графическом построении последней пары характеристик удобно использовать логарифмический масштаб, откладывая по оси абсцисс частоту в логарифмическом масштабе, а по оси ординат:

а) усиление в децибелах для амплитудной частотной характеристики;

б) угол  в радианах или градусах для фазовой характеристики.

3.2. ОБОСНОВАНИЕ МЕТОДА

Пусть на вход исследуемой системы поступает комплексное гармоническое воздействие

. (3.3)

Тогда установившийся входной сигнал системы определится как произведение частотной характеристики на входной сигнал

(3.4)

.

Сопоставление соотношений (3.3) и (3.4) показывает, что, проходя через стационарную линейную систему (звено), косинусоидальная (или синусоидальная) составляющая входного сигнала усиливается в раз, а её фаза сдвигается на угол . Это обстоятельство позволяет определять частотную характеристику одним из экспериментальных методов, исследуя реакцию системы на реальное гармоническое воздействие . Последнее может быть подано, например, с генератора гармонических колебаний. Так на вход исследуемого динамического звена с выхода генератора гармонических колебаний подается напряжение постоянной амплитуды при изменении частоты от 0 до бесконечности (практически этот диапазон равен полосе существенных частот звена). Одновременно этот сигнал подается на вход X электронного осциллографа для измерения его величины. Выходной сигнал динамического звена подается на вход Y – для измерения его величины и фазы.

Величина модуля и фаза частотной характеристики определяются с помощью осциллографа по форме и размерам фигуры Лиссажу.

Рассмотрим фигуру Лиссажу, полученную на экране осциллографа при подаче на его клеммы горизонтальной и вертикальной разверток входного и выходного сигналов звена соответственно (рис. 3.2).

Б удем считать, что масштаб по осям экрана Х и У выбран одинаково. В силу изложенного в предыдущем пункте, математическая запись входного и выходного сигналов имеет вид

; (3.5)

. (3.6)

На экране осциллографа амплитуды и изображены соответст­венно половинками отрезков А и В, т.е.

; , (3.7)

где М – масштаб экрана.

Поэтому модуль частотной характеристики для фиксированной час­тоты  может быть найден, как отношение этих отрезков:

. (3.8)

Сдвиг фазы  находят следующим образом. После подстановки соотношение (3.6) дает

. (3.9)

Из соотношения (3.9) вытекает, что в масштабе экрана ос­циллографа выражается отрезком , т.е.

. (3.10)

Отсюда следует (см. (3.9), (3.10), (3.7)), что для фиксированной частоты сдвиг фаз может быть найден по формуле

. (3.11)

В лабораторной работе формулы (3.8) и (3.11) могут быть приняты за исходные при экспериментальном определении частотных ха­рактеристик исследуемых звеньев.

3.3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1 . Собрать схему получения частотных характеристик звеньев со­гласно рис. 3.3. В качестве модели исследуемого звена (блок ) собрать схему моделирования апериодического звена (рис. 2.3,а).

2. Удалить перемычку управления яркостью луча электронного ин­дикатора. Включить 1–й режим работы АВК–6 .

3. После проверки набранной схемы преподавателем включить АВК–6 кнопкой "СЕТЬ". Установить амплитуду сигнала треугольной формы в соответствии с максимальной разверткой измерительных отрезков и вертикальной оси на экране электронного индикатора.

4. Установить коэффициенты и .

5.Произвести необходимые измерения для экспериментального по­лучения частотных характеристик исследуемого звена:

изменяя амплитуду сигнала синусоидальной формы, установить удобный для измерений масштаб (в процессе замеров его можно ме­нять); изменяя чистоту генератора, произвести измерения отрезков А, В и С (рис. 3.2 ), занося результаты в таблицу вида табл. 3.1. Из­мерения производить по цифровому вольтметру, перемещая измери­тельные отрезки на необходимый уровень делителем Д (рис. 3.3 ). Количество точек замеров должно быть достаточным для воспроизве­дения всей кривой АФЧХ (10 – 15 точек). Интервал частот между замерами можно менять.

Таблица 3.1

Замер	мс	, в	, в	, в

6. Собрать схему моделирования реального дифференцирующего звена (рис. 2.3,б) и подключить к схеме (рис. 3.3) . Не изменяя положения регуляторов и повторить п. 5.

7. Собрать схему моделирования колебательного звена (рис.2.3, в) и подключить к схеме. Не изменяя положения регуляторов и повторить п. 5.

8. По полученным данным, используя формулы (3.8) и (3.11), посчитать , , а также ; ; . Результаты занести в табл. 3.2.

Таблица 3.2

Замер	f, Гц	,

9. Построить экспериментальные частотные характеристики звень­ев: амплитудно-частотную, фазочастотную, логарифмическую ампли­тудную, вещественную и мнимую.

Вывести соотношения для частотной характеристики каждого из исследуемых звеньев, взяв за основу выражения для их переда­точных функций. Рассчитать и построить теоретические кривые амплитудно-частотной, фазочастотной, логарифмических амплитудной и фазовой характеристик, а также вещественной и мнимой на одних графиках с экспериментальными кривыми (результаты расчета свести в таблицу вида табл. 3.2). Сравнить их.

3.4.СОДЕРЖАНИЕ ОТЧЕТА

1.Краткое описание задачи и метода исследования.

2. Схемы моделирования звеньев и схема получения частотных ха­рактеристик.

3. Результаты эксперимента, сведенные в таблицу.

4. Результаты расчета по экспериментальным данным, сведенные в таблицу.

5.Выведенные соотношения для теоретического построения частотных характеристик.

6.Результата расчета по теоретическим данным, сведенные в таблицу.

7.Графики теоретических и экспериментальных кривых частотных характеристик.

8.Выводы о работе.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Воронов А. А. Основы теории автоматического управления: Автоматическое регулирование непрерывных линейных систем. М.: Энергия, I960. – 310 с.

2. Воронов А. А. Основы теории автоматического регулирования и управления. – М.: Высш. шк., 1977. – 618 с.

З. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. – М.: Наука, 1972. –768 с.

4. Попов Е.П. Теория линейных систем автоматического регу­лирования и управления. – М.: Наука, 1978. – 256 с.

5. Архангельский Е.А. Моделирование на аналоговых вычислительных машинах, –л.: Сергия, 1972. – 308 с.

6. Алексаков Г.Н., Гаврилин В.В., Федоров Э–А» Методичес­кие рекомендации по работе с персональным –аналоговым компьютером АВК–6.(Ч.1–Ч.6).– М.: Инженерный центр МИФИ, 1989. – 285 с.

Учебное издание

Методические указания к выполнению лабораторных работ по курсу "Теория автоматического управления"