1) Высказыванием называют любое повествовательное выражение, о котором можно сказать истинно оно или ложно.

Существует высказывание, которое при определенных условиях, является истинным, а в других условиях ложным, такие высказывания называют переменными.

С высказываниями можно выполнить следующие логические операции:

- дизъюнкция АVB – высказывание ложно только тогда, когда оба исходных высказывания ложно.

- конъюнкция АВ – высказывание истинно только тогда, когда оба исходных высказывания истинно.

- отрицание - высказывание истинно тогда, когда исходное высказывание ложно и наоборот.

- импликация А=>В(из А следует В, если А то В) – высказывание ложно только в одном случае, когда первое высказывание истинно, а второе ложно.

- эквивалентность АВ(А эквивалентен В) – высказывание истинно тогда и только тогда, когда оба высказывания вместе истинно или вместе ложно.

2) Формула логики. Понятие формулы логики вводится индуктивно: а)любое высказывание – формула; б)если А,В – формулы, то , АVB, АВ, А=>В, А=>В, а так же выражения со скобками так же являются формулами. Логическим значением формулы, называют истинность ее или ложность.

Таблицей истинности формулы логики называют таблицу из двух столбцов, в первом приводятся все возможные логические значения входящих в формулу переменных, во втором соответствующие логические значения формул.

x	y	z	x =>z
0 0 0 1 1 1 1 1	0 0 1 0 0 0 1 1	0 1 0 0 0 1 0 1	1 1 1 1 0 1 1 1

Тождественно истинная формула (тавтология) – всегда истинное высказывание АVВ.

Тождественно ложная формула (противоречие) – всегда ложное высказывание (АVВ)

3) Две формулы называются равносильными, если у них одинаковые таблицы истинности. Для получения раносильных формул используют следующие законы логики( тавтологии).

1) Идемпотентность AVA=A; AA=A

2) Коммутативность AVB=BVA; AB=BA

3) Ассоциативность (AVB)VC=AV(BVC); (AB)C=A(BC)

4) Дистрибутивность AVBC=(AVB)(AVC); A(BVC)=ABVAC

5) Закон двойного отрицания =A

6) Закон де Моргана ;

7) Склеивание ABVA =A; (AVB)(AV )=A

8) Поглощение AVAB=A; A(AVB)=A

9) Действие с константами AV0=A; AV1=1; A0=0; A1=A

10) Исключение импликации A=>B= VB

11) Исключение эквивалентности AB=ABV

4) n-мерным булевым вектором называют любой набор n-переменных, каждая из которых может принимать только два значения(0 или 1).

2 булевых вектора отличающиеся одной координатой называются соседними.

Пары векторов все координаты, которых противоположны называются противоположными.

Существует 8 трехмерных булевых векторов, которые можно изобразить в пространственной системе координат, вершинами 1-ого куба.

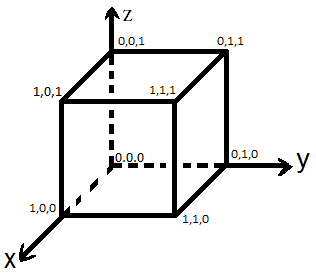
По аналогии с рассмотренным, множество всех n-мерных булевых векторов называют n-мерным единичным кубом.

Пусть имеется произвольный k-мерный булев вектор. Получим из него (k+1)-мерный вектор добавив еще одну координату(x1,x2,…,xk,0)=>(x1,x2,xk,1). Т.о. из каждого k-мерного вектора можно получить 2(k+1)-мерных векторов. Значит с добавлением одной координаты вектора , число векторов увеличивается ровно в два раза. Тогда число всех n-мерных булевых векторов равно .

5) Булевой функцией называют отображение, которое каждому двоичному вектору ставит соответствие 0 или 1.

Булеву функцию можно задавать таблицей, в ее первом столбце перечисляют все возможные булевы векторы, а во втором значение функции на каждом из векторов.

Так как набор значений булевой функции n-переменных, состоит из , нулей и единиц, то она представляет собой - мерный булев вектор, поэтому число различных булевых функции n-переменных, равно числу различных -мерных векторов, т.е. равно .

6) Выпишем все булевы функции 2 переменных.

x	y	0	xy	x	x	y	y	x+y	xVy	x↓y	xy		y=>x		x=>y	x│y	1
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Из приведенной таблицы видно, что основными логическими функциями являются:

-константы 0,1;

-конъюнкция &,●;

-дизъюнкция V;

-отрицание ¯;

-импликация =>;

-эквивалентность ;

-сумма Жегалкина x+y;

-стрелка Пирса ↓;

- штрих Шеффера │;

Булевы функции обладают теми же свойствами что и аналогичные логические операции.

7) Элементарной конъюнкцией называют конъюнкцию переменных или их отрицание.

Элементарная конъюнкция называется совершенной, если каждая переменная входит в нее ровно 1 раз с отрицанием или без него.

СДНФ называют запись булевой функции в виде дизъюнкций совершенных элементарных конъюнкций, каждая из которых встречается только 1 раз.

Элементарной дизъюнкцией называют дизъюнкцию переменных или их отрицание.

Элементарная дизъюнкция называется совершенной, если каждая переменная входит в нее ровно 1 раз с отрицанием или без него.

СКНФ называют конъюнкцию совершенных элементарных дизъюнкций.

8) ДНФ называют минимальной , если оно содержит наименьшее количество логических операций. Записав функцию в виде СДНФ или СКНФ, можно попытаться с помощью преобразований по закону логики, преобразовать ее к минимальной форме, но это не всегда может получиться.