Количество информации

Основные умения: осуществлять измерение информации и расчет энтропии; использовать знания об измерении энтропии и количестве информации в практической деятельности педагога.

Основные понятия.

Мощность алфавита – это количество различных символов, которые можно получить с помощью кодовой цепочки, состоящей из I битов. Биты для измерения информации используются тогда, когда каждый элемент цепочки может принимать 2 устойчивых состояния.

N=2^I (1)

Информационная емкость символа, т.е. количество информации, которое несет один знак, зависит от количества символов в алфавите:

I = ­ log₂ N (2)

Количество информации, которое содержит сообщение V, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак I, умноженному на количество знаков в сообщении n.

V=In (3)

Пример 1: Каждый символ закодирован одним байтом. Оцените информационный объем (в битах) следующего предложения в этой кодировке:

В одном килограмме 1000 грамм.

Решение.

Количество символов в фразе n=30. Каждый символ равен 1 байту, следовательно, фраза будет занимать 30 байт информации, что составит:

I = 30 · 8 =240 бит информации.

Пример 2: Пользователь компьютера, хорошо владеющий навыками ввода ин­формации с клавиатуры, может вводить в минуту 100 знаков. Мощ­ность алфавита, используемого в компьютере, равна 256. Какое ко­личество информации в байтах может ввести пользователь в компьютер за 12 минут?

Решение.

Найдем количество символов n, которые пользователь может ввести за 12 минут: n=12100=1200 символов. Информационная емкость символа при мощности N=256 составит: I = ­ log₂ 256=8 бит=1 байт на 1 символ. Следовательно, количество информации, которое может ввести пользователь V=1байт1200=9600 =1200 байт.

Информация может рассматриваться как уменьшение неопределенности состояния системы, а количество информации определяется как разность энтропий:

I(X)=H(X)-H'(X). (4)

Для случая, когда система имеет n состояний, и все они равновероятны, используется формула Хартли:

I = ­ log₂ n. (5)

Пример 3: Световое табло состоит из лампочек, каждая из которых может находиться в двух состояниях ("включено" или "выключено"). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

Решение.

Количество сигналов n=50, лампочки могут находиться в 2-х состояниях, следовательно, необходимо найти показатель степени (целое число), в которое необходимо возвести 2, чтобы получилось число большее 50, и наиболее близко к нему расположено: I = log₂ 50  6; минимально потребуется 6 лампочек, т.к. с помощью 5-ти лампочек можно закодировать лишь 32 сигнала.

Из формул (4) и (5) можно получить:

I=log₂n₁–log₂n₂=log₂ n₁/ n₂. (6)

Пример 4: В стопке дисков находятся 8 дисков с прикладными программами, 6 дисков с обучающими программами и 10 игр. Какое количество информации получено, если известно, что случайно извлеченный диск – это диск с обучающей программой?

Решение.

Первоначально количество исходов извлечения диска n₁=8+6+10=24, после получения сообщения n₂=6, можно применить формулу 6:

I = log₂ 24 – log₂ 6 = log₂ 24/6 = log₂4 =2 бита информации.

Под собственной информацией будем понимать информацию, содержащуюся в данном конкретном сообщении, которое дает получателю информацию о возможности существования конкретного состояния системы. Тогда количество собственной информации, содержащееся в сообщении S_i, определяется как:

I(S_i)= –log ₂ P(S_i) (7)

Собственная информация имеет следующие свойства:

1. Неотрицательна.

2. Чем меньше вероятность возникновения сообщения, тем больше информации оно содержит.

3. Информация равна 0, если вероятность возникновения сообщения равна 1.

4. Количество собственной информации нескольких независимых сообщений равно их сумме.

I(X_i, Y_i)= –log ₂ P(X_i) – log ₂ P(Y_i)= I(X_i)+ I(Y_i).

Пример 5: У скупого рыцаря в сундуке золотые, серебряные и медные монеты. Каждый вечер он извлекает из сундука одну из лежащих в нем 96 монет, любуется ею, и кладет обратно в сундук. Количество информации, содержащееся в сообщении «Из сундука извлечена серебряная монета», равно 4 бита. Информационный объем сообщения «Из сундука извлечена золотая монета» равен 5 бит. Сколько медных монет было в сундуке.

Решение.

Обозначим сообщение «Из сундука извлечена золотая монета» за S₁; а сообщение «Из сундука извлечена серебряная монета» за S₂; k₁ – количество золотых монет; k₂ – количество серебряных монет; k₃ – количество медных монет; общее количество монет k = k₁+ k₂ + k₃=96.

По формуле (7) I(S_i)= -log₂ P(S_i) = log₂

и соотношения можно найти:

I(S₁)=5 бит, ;

– в сундуке 3 золотых монеты

I(S₂)=4 бита, ;

– в сундуке 6 серебряных монет

k₃ = k – ( k₁+ k₂ )= 96 – (6+3) =87 – в сундуке 87 медных монет.

Теорема Шеннона. Если система X обладает дискретными состояниями, их количество равно n, а вероятность нахождения в каждом из состояний p(A₁), p(A₂) ,…, p(A_n), то энтропия система H(X) равна:

(8)

Свойства энтропии

1. H=0 в двух случаях: Какая-либо из P(A_j)=1, следовательно, все остальные P(A_i)=0 (i  j) или все P(A_i)=0.

2.  и  независимые опыты: H()=H()+H().

3.  и  зависимые опыты: H()=H()+H_(), где

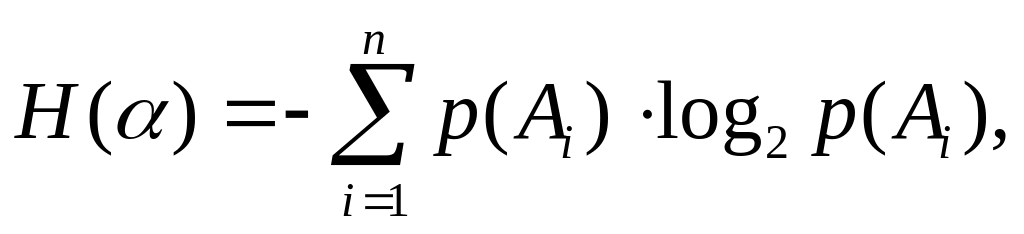
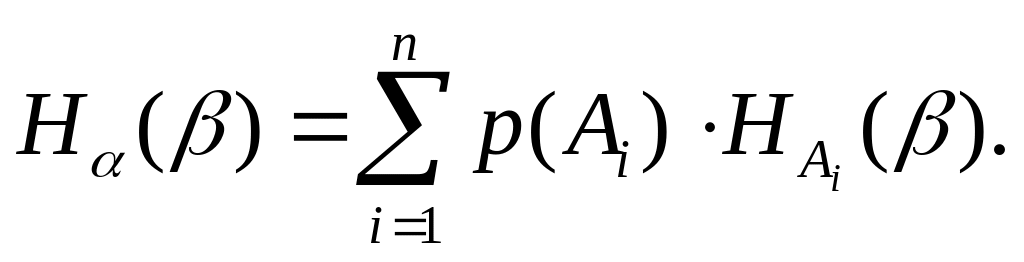
Пример 6: Имеются 2 ящика, в каждом по 12 шаров. В первом 3 белых, 3 черных и 6 красных. Во втором – каждого цвета по 4. Опыт состоит в извлечении по одному шару из каждого ящика. Найти энтропию извлечения.