
- •1. Задание № 46
- •Общие указания
- •Образец оформления титульного листа
- •Математическая статистика.
- •Теория вероятностей
- •Тема 1. Классическая формула
- •Тема 2. Основные теоремы
- •Тема 3. Дискретная случайная величина
- •Тема 4. Непрерывная случайная величина
- •Математическая статистика
- •Тема 5. Статистическое распределение выборки. Точечные и интервальные оценки.
- •Тема 6. Доверительный интервал. Критерий Пирсона
- •Тема 7. Элементы теории корреляции
- •Задачи Семестрового задания №3 (Контрольной работы №3)
- •Задание №
- •Задание 2
- •Задание 3
- •Задание 2
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Задание 9
- •Задание 10
- •Приложение. Таблицы функций
- •Литература
- •454091, Г.Челябинск, ул.Свободы 155/1
Тема 3. Дискретная случайная величина
Литература
Забейворота В.И., Волохова К.И. Математика в экономике (Теория вероятностей). Учебное пособие (параграфы 9-10). УрСЭИ, Челябинск, 2001
При изучении темы 3 и темы 4 и следует обратить особое внимание на свойства и взаимосвязь функции распределения и плотности распределения случайной величины, на их использование при определении вероятностей различных событий, связанных со случайной величиной. В этом смысле важное место должны занять экономические приложения рассматриваемых понятий.
Законом распределения дискретной случайной величины является ряд распределения
x1 |
x2 |
... |
xn |
... |
p1 |
p2 |
... |
pn |
... |
рi=P(X=xi), где i=1;2;...;n;...
Числовые характеристики дискретной случайной величины:
1)
математическое ожидание
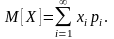 (если же дискретная случайная величина
Х имеет n
возможных значений, то
(если же дискретная случайная величина
Х имеет n
возможных значений, то
 ),
),
2)
дисперсия
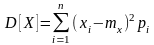 или
или
 в
зависимости от того, конечно или
бесконечно число возможных значений
дискретной случайной величины.
в
зависимости от того, конечно или
бесконечно число возможных значений
дискретной случайной величины.
Для вычислений удобнее пользоваться формулой Dx=M[X2]-m2x .
3)
среднее квадратическое отклонение
sх= .
.
Функция
распределения дискретной случайной
величины F(x)=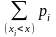 ;
т.е. суммируем те pi,
для которых xi<x.
;
т.е. суммируем те pi,
для которых xi<x.
3Пример 6. Магазин получает товар от трех независимо работающих фирм. Вероятность поставки товара от первой фирмы равна 0,4, от второй - 0,3, от третьей –0,6. Составить распределение случайной величины Х - числа полученных поставок, найти числовые характеристики и функцию распределения этой случайной величины.
Решение.
Случайная величина Х - число полученных поставок может принимать значения: 0,1,2,3. Найдем вероятности принятия каждого из этих значений.
Обозначим через Аi (независимые события) – получение поставки товара с i-ой фирмы, где i=1,2,3, через pi-вероятность события Ai.
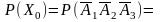 |
т.к. события А1,А2,А3
независимы, то и события
|
т.к. события А1,А2,А3
независимы, то и события
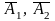 ,
, независимы |
независимы |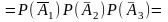 (1-p1)(1-p2)(1-p3)=q1q2q3=
(1-0,4)(1-0,3)(1-0,6)=0,168.
(1-p1)(1-p2)(1-p3)=q1q2q3=
(1-0,4)(1-0,3)(1-0,6)=0,168.
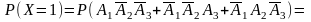 |
события
|
события
 ,
,
 ,
,
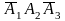 несовместны|
несовместны|
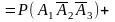
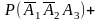
 )=p1q2q3+q1q2p3+q1p2q3=
)=p1q2q3+q1q2p3+q1p2q3=
=0,4×(1-0,3)×(1-0,6)+(1-0,4)×(1-0,3)×0,6+(1-0,4)×0,3×(1-0,6)=0,436.
Р(Х=2)=Р(А1А2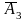 )+Р(А1
)+Р(А1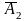 А3)+Р(
А3)+Р(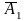 А2А3)=р1р2q3+р1q2р3+q1р2р3=
А2А3)=р1р2q3+р1q2р3+q1р2р3=
=0,4×0,3×(1-0,6) + 0,4×(1-0,3)×0,6+(1-0,4)×0,3×0,6=0,324.
Р(Х=3)=Р(А1А2А3)=Р(А1)×Р(А2)×Р(А3)=0,4×0,3×0,6=0,072.
Следовательно,
X |
0 |
1 |
2 |
3 |
P |
0,168 |
0,436 |
0,324 |
0,072 |
Проверим
условие нормировки:
 .
.
Действительно, 0,168+0,436+0,324+0,072=1.
Найдем М[X] и D[X].
=0×0,168+1×0,436+2×0,324+3×0 072=1,3.
Dx=M[X2]-m2x
=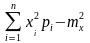 =0×0,168+1×0,436+4×0,324+9×0,072-1,32
=
0,69.
=0×0,168+1×0,436+4×0,324+9×0,072-1,32
=
0,69.
sх=
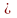 0,83.
0,83.
Найдем функцию распределения F(x).
Т.к. F(x)= , то
F(x)=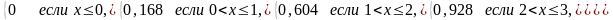 4
4
Вопросы для самопроверки.
Случайная величина. Спектр. Дискретная случайная величина.
Закон распределения дискретной случайной величины. Условие нормировки. Многоугольник распределения.
Функция распределения. Вероятность попадания случайной величины на промежуток и в точку.
Математическое ожидание, дисперсия и среднее квадратическое отклонение дискретной случайной величины; формулы для их нахождения.
Биноминальное распределение и его числовые характеристики.
Распределение Пуассона и его числовые характеристики.
