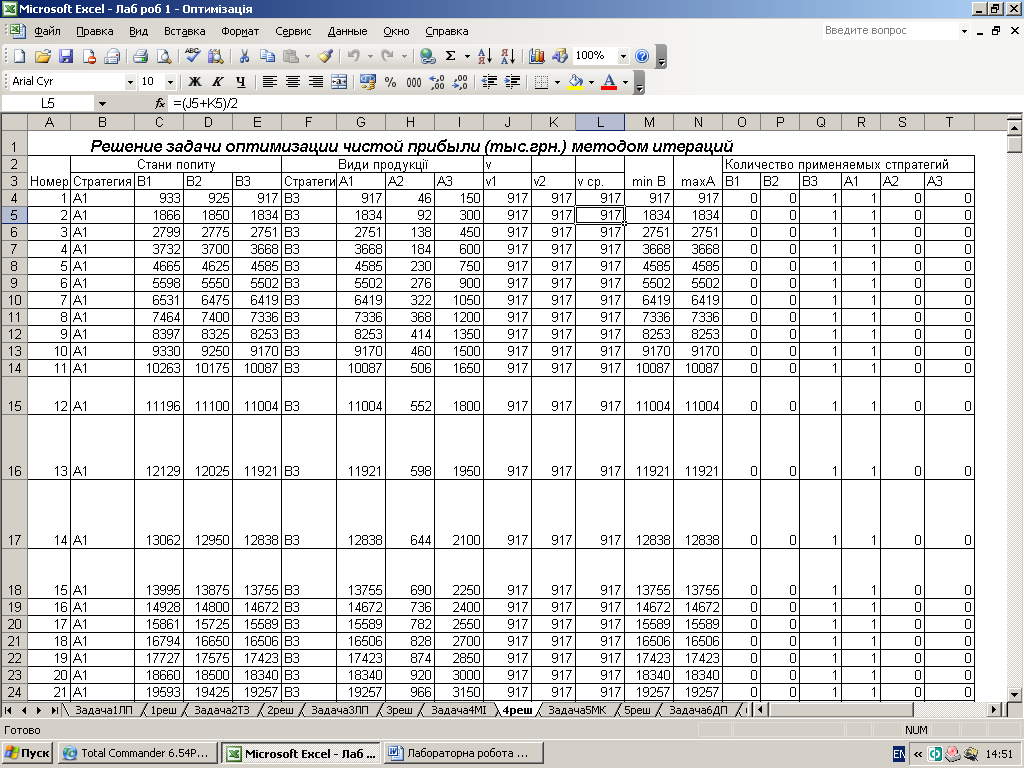
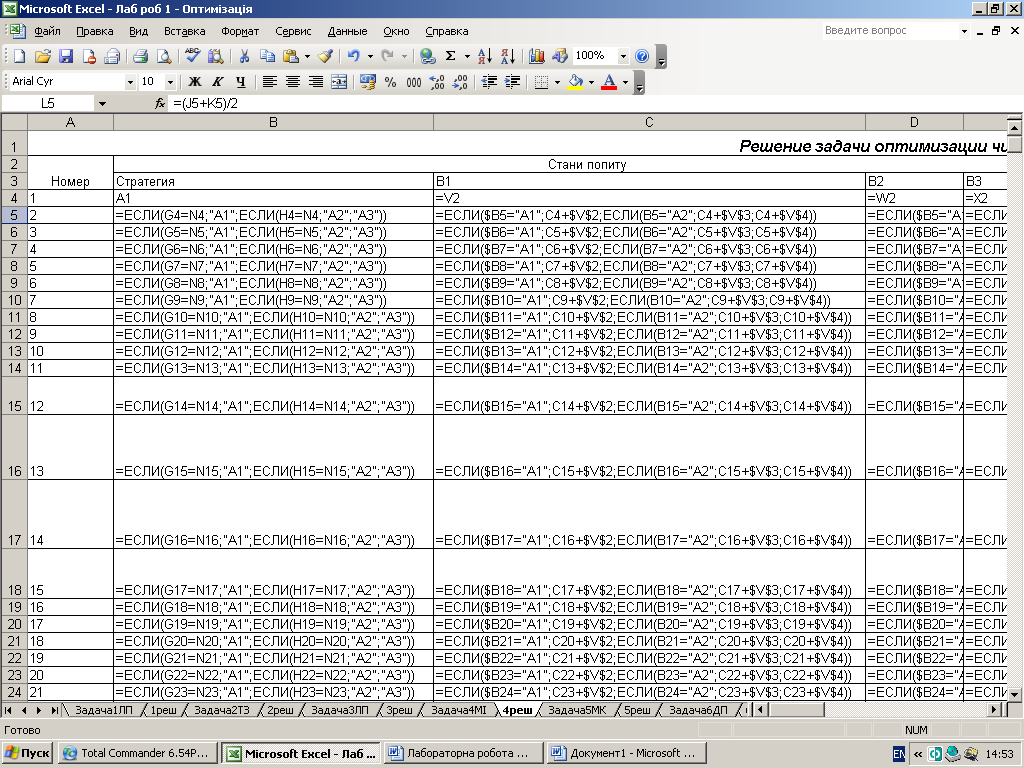
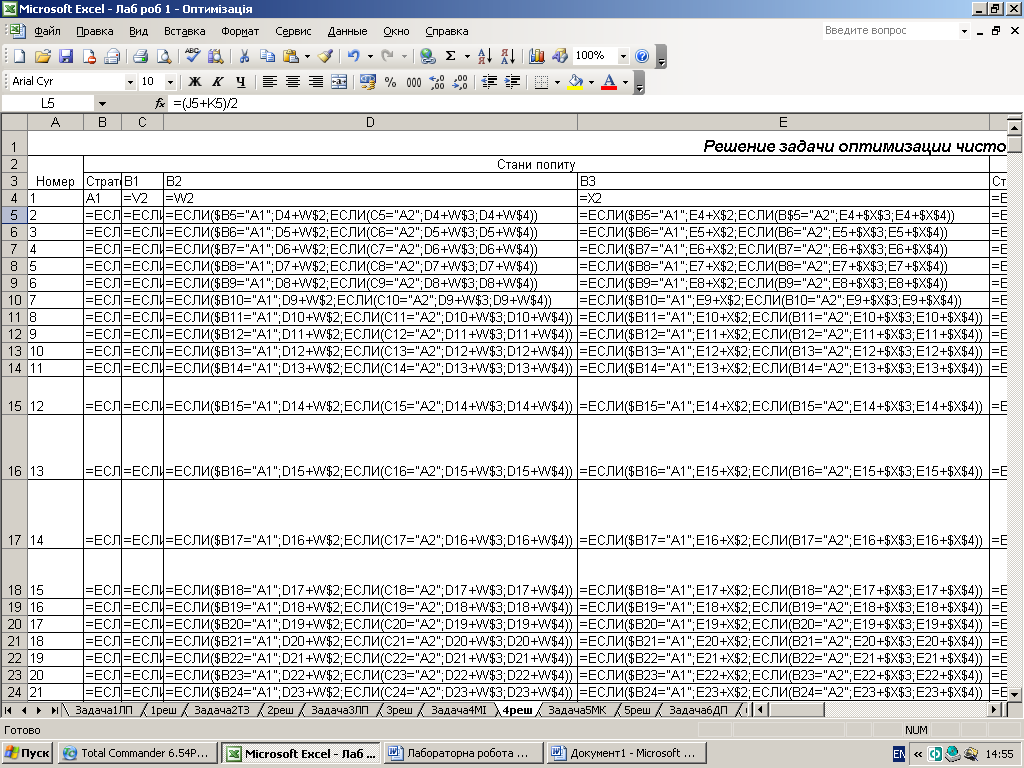
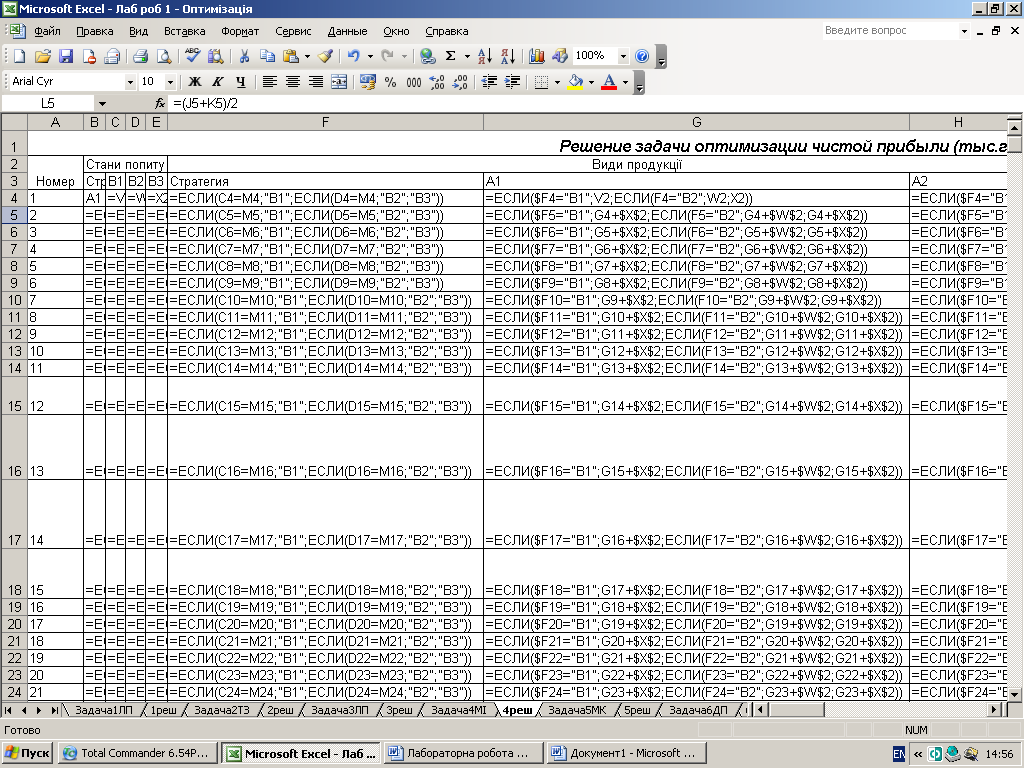
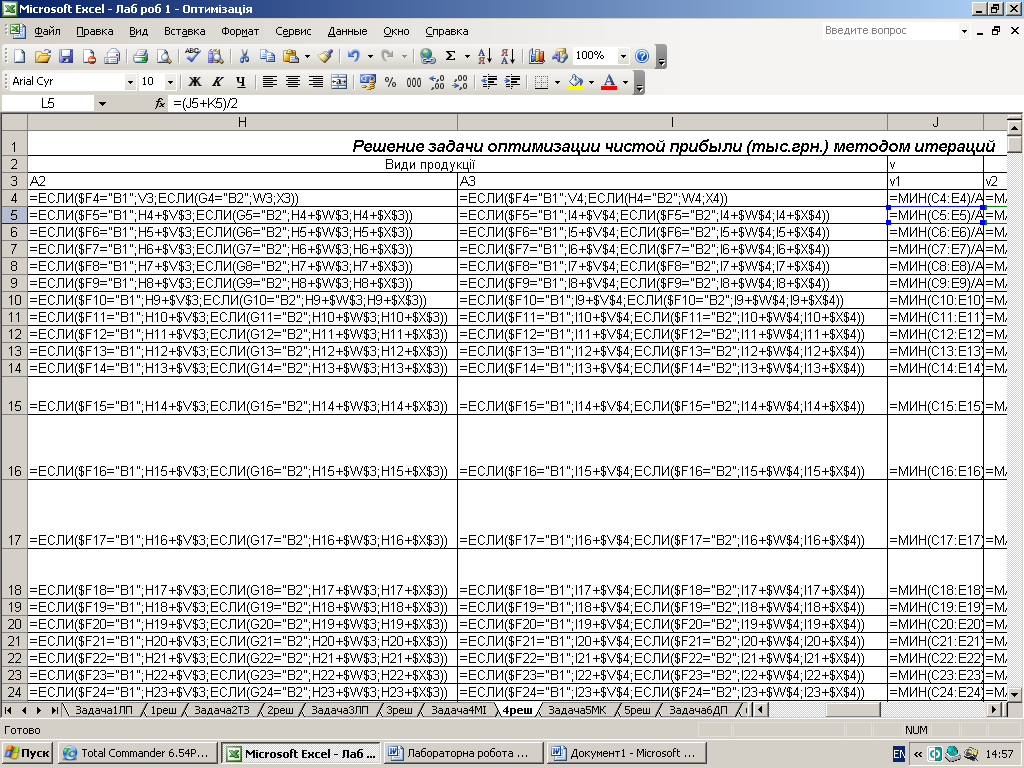
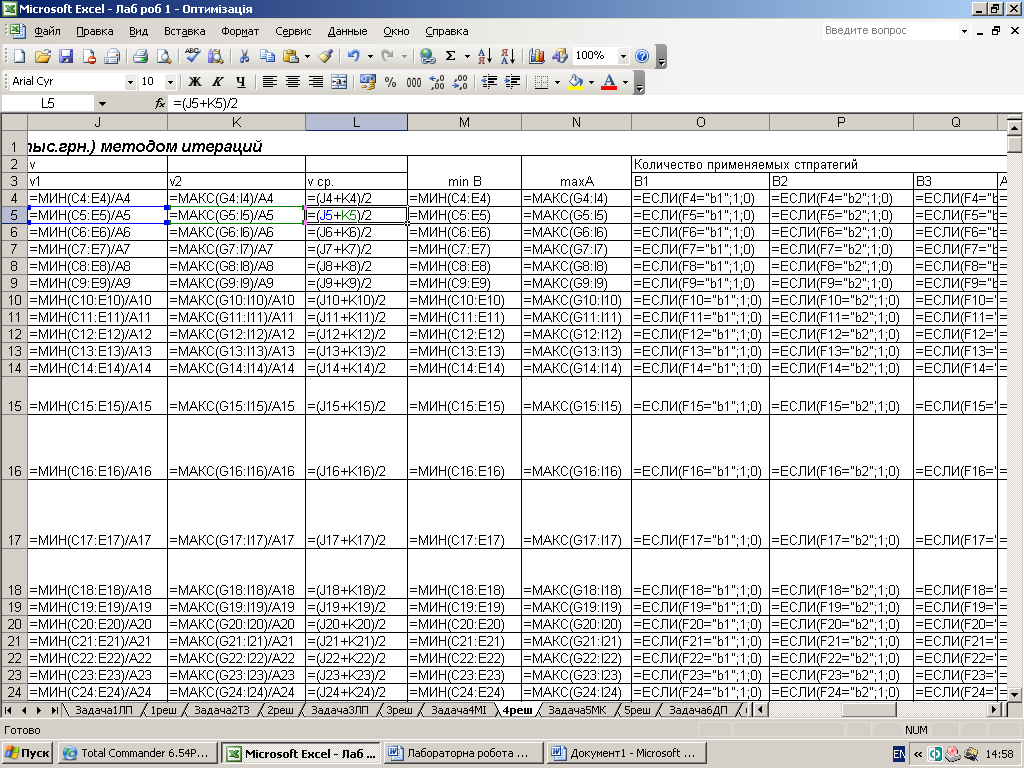
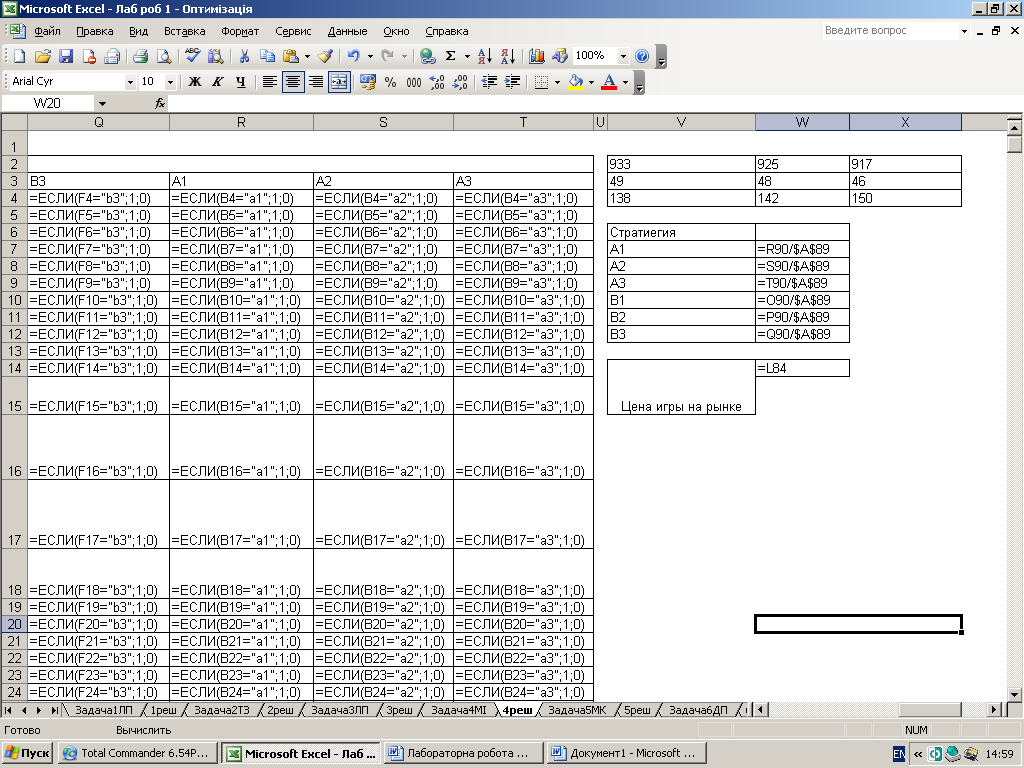
Наближений метод рішення матричних ігор.

В основі методу ітерацій є гіпотеза про те, що «матрична гра» складається з великої кількості партій, що гравці в своїх стратегіях як-би накопичують досвід вже тих партій, що відбулися. При необмеженому збільшенні числа партій ці наближені змішані стратегії будуть наближуватись до оптимальних, а середні виграші будуть наближуватись до ціни гри(середній виграш вцілому).

Нехай відбувається гра розміру .

A\B	B1	…	Bs	…	Bt	…	Bn
A1			A1s
…
Ak	ak1	…	aks	…	ats	…	ans
…
Al	al1	…	als	…		…	als
…
Am			ams	…		…

Допустимо, що в першій партії А вибрав Ак. Виграш – одне зі значень строки ak1…akn. Гравець В при Ак відповідає тією стратегією, при якій його програш мінімальний - нехай це . - найменший з накопичених виграшів гравця А за партій, поділений на число партій. - найбільший з накопичених програшів гравця В, поділений на число партій . - середнє арифметичне. 2 партія – А відповідає стратегією гравцю В, яка забезпечить більший виграш, коли В не поміняє стратегію . Нехай це , тоді його виграш з рядка . - це сумарний виграш за першу і другу партію – накопичений виграш. Гравець В вибирає , що мінімізує програш. Нехай зіграли партій. За ці партій гравець А стратегію Аі застосував разів, разів. Можна підрахувати імовірність застосування .