
Работа 2 Метод наименьших квадратов
.pdf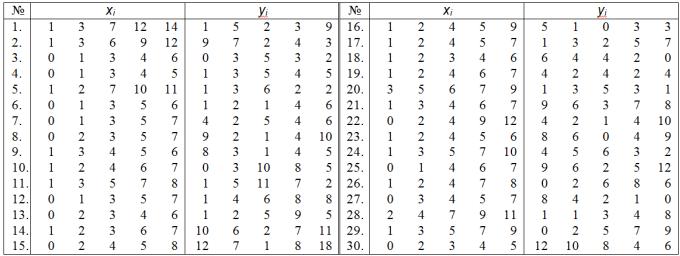
2. Аппроксимация дискретных данных методом наименьших квадратов
2.1 Цель работы
Целью работы является получение навыков аппроксимации дискретных данных полиномом и исследование погрешностей аппроксимации в зависимости от степени полинома.
2.2Задание
1.Аппроксимировать таблично заданные значения неизвестной функции методом наименьших квадратов полиномами 1, 2, 3 и 4 степеней. При этом:
Для полиномов 1, 2, 3 и 4 степеней найти их коэффициенты путем решения систем линейных уравнений (для полинома второй степени также выполнить это вручную).
Для полиномов 1 и 2 степени также найти коэффициенты с помощью функции regress.
Для полинома 3-й степени также найти коэффициенты с помощью функции linfit.
Для полинома 4-й степени также найти коэффициенты с помощью функции interp.
2.Построить совмещенный график заданных узлов и всех полиномов.
3.Построить график суммы квадратов отклонений полиномов во всех узлах
взависимости от степени полинома.
Варианты заданий
2.3 Теоретические сведения
Метод наименьших квадратов применяют, когда необходимо вывести формулу аппроксимирующей кривой, описывающей некоторую зависимость, полученную в результате, например, эксперимента. Поскольку экспериментальные данные получают, как правило, с некоторой погрешностью, то нет смысла использовать, например, интерполяционный многочлен Лагранжа,
1

всегда проходящий через узлы интерполяции. В этом случае обычно проводят аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время учитывает исследуемую закономерность, сглаживая случайные выбросы результатов эксперимента. В качестве аппроксимирующей функции может использоваться линейная комбинация F ( x) любых функций:
F( x) a0 f0 ( x) a1 f1 ( x) an fn ( x)
где f0 ( x), f1 ( x), fn ( x) - набор любых функций, называемых базисными; a0 ,a1 , ,an - набор коэффициентов.
Довольно часто в качестве базисных функций используют комбинацию из степенной последовательности аргумента f0 ( x) 1, f1 ( x) x, , fn ( x) xn . При
этом аппроксимирующая функция будет являться алгебраическим полиномом. Именно этот случай и рассматривается в работе.
Пусть некоторая функция задана таблицей значений yi в узлах xii 0,1,2, , m , где m 1 – количество узлов.
Требуется определить коэффициенты a0 ,a1 , ,an полинома
|
|
P( x) a |
0 |
a |
x a |
n |
xn |
|
|
|
|
|
1 |
|
|
|
|
||
таким образом, чтобы |
сумма S |
квадратов |
отклонений |
полинома P( x) от |
|||||
значений |
yi аппроксимируемой |
|
функции |
в |
|
заданных |
точках была бы |
||
минимальной, т.е. |
|
|
|
|
|
|
|
|
|
|
|
m |
an xin yi 2 min |
|
|||||
|
S a0 a1 xi |
|
|||||||
|
|
i 0 |
|
n m, |
|
|
|
|
|
Если |
степень |
полинома |
|
то |
|
искомый |
полином будет |
||
интерполяционным и пройдет через все узлы и отклонения будут нулевыми.
Стремясь понизить степень полинома, |
принимают |
n m , при этом в общем |
||
случае |
аппроксимирующая |
кривая не |
будет проходить через заданные точки |
|
xi , yi . |
Сумма квадратов |
отклонений |
зависит от |
коэффициентов полинома |
a0 , a1 , , an . Поскольку функция S принимает только положительные значения и имеет минимум, вычислим частные производные по всем переменным a0 , a1 , , an и приравняем их нулю:
S 0, i 0,1,2, , n
ai
Получаем систему уравнений:
2
|
|
|
S |
|
m |
|
n |
||
|
|
|
|
|
|
|
2 a0 a1 xi an xi yi 0 |
||
|
|
a0 |
|||||||
|
|
|
|
i 0 |
|
|
|||
|
S |
|
|
m |
|
|
|||
|
|
2 a0 |
a1 xi |
an xin yi xi 0 |
|||||
|
|
|
|||||||
|
|
a1 |
|
i 0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
||
|
|
|
|
m |
|
|
|||
|
|
2 a0 |
a1 xi |
an xin yi xin 0 |
|||||
|
|
||||||||
|
an |
|
i 0 |
|
|
||||
Выполнив суммирование, собрав коэффициенты при каждом a0 , a1 , , an и перенеся не содержащие их суммы в правую часть, получим СЛАУ относительно неизвестных a0 , a1 , , an :
|
|
|
n |
|
|
|
|
m |
m |
m |
|
a0 m 1 a1 xi |
an xi |
yi |
|||
|
|
i 0 |
i 0 |
i 0 |
|
m |
m |
m |
m |
||
a0 xi a1 xi2 an xin 1 xi yi |
|||||
|
i 0 |
i 0 |
i 0 |
i 0 |
|
|
|||||
|
|
|
|
||
|
m |
m |
m |
m |
|
a0 |
xin a1 |
xin 1 an xi2 n xin yi |
|||
|
i 0 |
i 0 |
i 0 |
i 0 |
|
В матричной форме эту систему можно записать как a C b , где:
|
|
|
|
|
|
n |
|
|
|
|
|
m |
|
m |
|
a0 |
|
m 1 |
xi |
|
xi |
|
|
|
|
i 0 |
|
i 0 |
|
||
|
|
m |
m |
|
m |
||
a1 |
|
|
xi |
xi2 |
xin 1 |
|
|
a |
|
; C |
i 0 |
i 0 |
|
i 0 |
; |
|
|
|
|
|
|
|
|
|
|
|
m |
m |
|
m |
|
an |
|
xin |
xin 1 |
xi2 n |
|
||
|
|
|
i 0 |
i 0 |
|
i 0 |
|
|
m |
|
|
yi |
|
|
i 0 |
|
|
m |
|
b |
xi yi |
|
|
i 0 |
|
|
|
|
m |
||
|
xin yi |
|
|
i 0 |
|
Решение этой системы позволяет найти все коэффициенты a0 , a1 , , an .
Для полиномиальной аппроксимации (регрессии) в MathCAD’е можно воспользоваться следующими встроенными функциями:
1.regress(x,y,k) – возвращает вектор коэффициентов a полинома, при этом всегда первые три компоненты вектора есть вектор вторых производных и являются параметрами для описываемой ниже
функции interp, а остальные компоненты и есть вектор коэффициентов a , где x - вектор данных аргумента, элементы которого должны быть расположены в порядке возрастания; y -
вектор значений того же размера; k - степень полинома (целое положительное число).
Функция regress позволяет, вычислив коэффициенты a0 , a1 , , an , построить полином и уже его использовать, например, для построения графика.
2.interp (s,x,y,t) – возвращает результат полиномиальной регрессии, где s - вектор вторых производных, созданный, например, предыдущей
3
функцией; x и y - то же, что и в предыдущей функции; t значение аргумента полинома.
Функция interp позволяет непосредственно вычислить значение при любом значении аргумента без построения полинома.
- текущее
полинома
3.linfit(x,y,F) – более универсальная функция, возвращающая вектор коэффициентов a линейной комбинации функций, где x и y - то же,
что и в предыдущей функции; |
F |
- вектор базисных функций |
f0 ( x), f1 ( x), fn ( x). Например, |
для |
нахождения алгебраического |
полинома степени n 2 необходимо записать F в следующем виде:
1 F xx 2
Функция linfit также позволяет непосредственно вычислить значение полинома при любом значении аргумента без построения полинома.
2.4 Пример выполнения работы
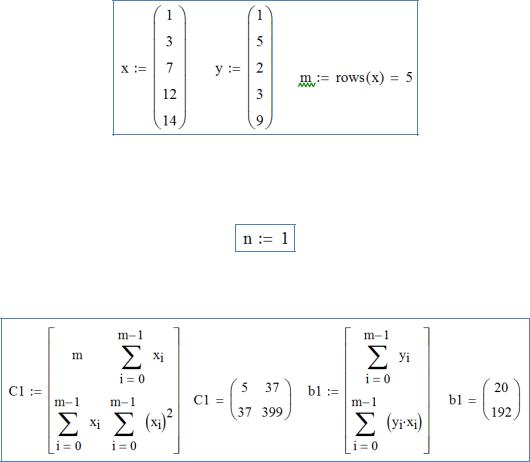
Рассмотрим выполнение лабораторной работы на примере первого задания. Вводим табличные данные в векторы узлов x и y и определяем количество
узлов.
Определяем коэффициенты и составляем полиномы для различных степеней n .
Полином 1-й степени
Задание степени полинома:
А) Нахождение коэффициентов аппроксимирующего полинома с помощью системы линейных уравнений.
Задание левой и правой части системы уравнений:
Решение системы линейных уравнений:
4

Задание аппроксимирующего полинома:
Б) Нахождение коэффициентов аппроксимирующего полинома с помощью функции regress.
Значения коэффициентов аппроксимирующего полинома совпадают с полученными ранее.
Задание аппроксимирующего полинома:
Полином 2-й степени
Задание степени полинома:
А) Нахождение коэффициентов аппроксимирующего полинома с помощью системы линейных уравнений.
Задание левой и правой части системы уравнений:
Решение системы линейных уравнений:
5

Задание аппроксимирующего полинома:
Б) Нахождение коэффициентов аппроксимирующего полинома с помощью функции regress.
Значения коэффициентов аппроксимирующего полинома совпадают с полученными ранее.
Задание аппроксимирующего полинома:
Полученный аппроксимирующий полином позволяет построить его график и найти его числовое значение при разных значениях t. Функция interp позволяет непосредственно вычислить значение полинома.
Пример нахождения числового значения аппроксимирующего полинома при t=4 двумя способами:
Полином 3-й степени
А) Нахождение коэффициентов аппроксимирующего полинома с помощью системы линейных уравнений.
Задание левой и правой части системы уравнений:
Решение системы линейных уравнений:
Задание аппроксимирующего полинома:
6

Б) Нахождение коэффициентов аппроксимирующего полинома с помощью функции linfit.
Составляем вектор-функцию F из линейной комбинации базисных функций.
Вычисляем вектор коэффициентов аппроксимирующего полинома.
Значения коэффициентов аппроксимирующего полинома совпадают с полученными ранее.
Задание аппроксимирующего полинома:
Функция linfit позволяет непосредственно вычислить значение полинома без представления его в явном виде.
Пример нахождения числового значения аппроксимирующего полинома при t=4 двумя способами:
Полином 4-й степени
Полином такой степени при заданных пяти узлах будет интерполяционным и должен пройти через все узлы.
Задание степени полинома:
А) Нахождение коэффициентов аппроксимирующего полинома с помощью системы линейных уравнений.
Задание левой и правой части системы уравнений:
7
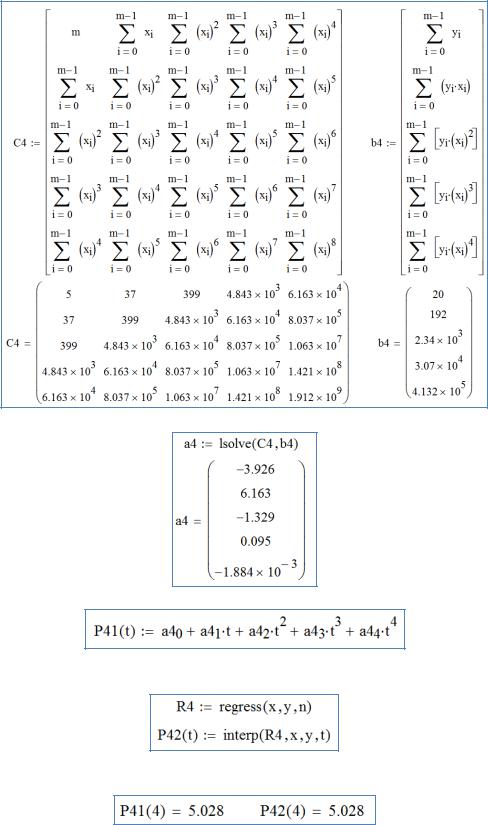
Решение системы линейных уравнений:
Задание аппроксимирующего полинома:
Б) Нахождение коэффициентов аппроксимирующего полинома с помощью функции interp.
Пример нахождения числового значения аппроксимирующего полинома при t=4 двумя способами:
Построим совмещенный график заданных узлов и всех полученных полиномов.
8

Найдем суммы квадратов отклонений d найденных аппроксимирующих полиномов различных степеней от табличных значений во всех узлах. Для этого составим программу.
График зависимости суммы квадратов отклонений полиномов во всех узлах от степени полинома.
Из приведенных графиков видно, что наилучший способ аппроксимации исходных данных – полиномом 3-й степени. При этом сумма квадратов отклонений во всех узлах будет наименьшей. Т.к. полином 4-й степени является интерполяционным, то для него сумма квадратов отклонений равна нулю.
9
2.5Содержание отчета
1.Титульная страница с названием работы.
2.Задание.
3.Цель работы и краткие теоретические сведения.
4.Выполненные задания. На отдельном листе ручной расчет коэффициентов аппроксимирующего полинома 2 порядка.
5.Выводы по проделанной работе.
2.6Контрольные вопросы
1.Какое должно быть соотношение между порядком аппроксимирующего полинома и количеством узлов таблицы значений функции?
2.Как вычисляются отклонения значений аппроксимирующего полинома и функции?
3.Из каких условий определяются коэффициенты аппроксимирующего полинома?
4.От чего зависит значение суммы квадратов отклонений?
5.Каковы основные этапы решения задачи аппроксимации методом наименьших квадратов?
6.Какие функции MathCAD решают задачу аппроксимации методом наименьших квадратов?
2.7Литература
1.Бахвалов Н.С. Численные методы. – М., Наука,1975. –632 c.
2.Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. – М., Наука,1976. –304 с.
3.Волков Е.А. Численные методы: Учебное пособие для вузов. – 2-е
изд. – М., Наука, 1987.
4.Копченова Н.В., Марон И.А. Вычислительная математика в примерах
изадачах. – М., Наука,1972.
10
