45. Циклы Отто и Дизеля.

Цикл Отто — термодинамический цикл, описывающий рабочий процесс двигателя внутреннего сгорания с воспламенением сжатой смеси от постороннего источника энергии, цикл бензинового двигателя

Цикл Дизеля — термодинамический цикл, описывающий рабочий процесс двигателя внутреннего сгорания с воспламенением впрыскиваемого топлива от разогретого рабочего тела, цикл дизельного двигателя.

46. Энтpопия как теpмодинамическая функция состояния. Энтропия иг. Физический смысл энтропии.

Функцию S можно представить в виде S1=S0+. Здесь 0 произвольно выбранное начальное состояние системы, а S0- приписанное ему произвольное значение для функции S. Разность значений S2-S1 не зависит от S0.

Свойства:1) определяется с точностью до постоянного слагаемого, физ. Смысл имеет только разность энтропий; 2)аддитивна, т.е общая энтропия составной системы равна сумме энтропий отдельных частей

Энтропия ИГ dQ=νCνdT+pdV

S=S0+νCν+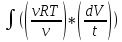=S0+νCνlnT+νRlnV

Наблюдаемая величина: ΔS=νCν ln(T2/T1)+ νRln(V2/V1) , S0 выбирается произвольно, но по некоторым правилам(аддитивности):S(A+B)=SA+SB. Произвольная постоянная S0: не меняется в зависимости от T и V, но может зависеть от ν-S0(ν)

Энтропия-это приведенное количество теплоты, кот получает ТД система при переходе из стандартного состояния( в кот значение S0 принято равным 0) в искомое состояние по отрезкам адиабат(адиабата может быть и одна)и изотерме.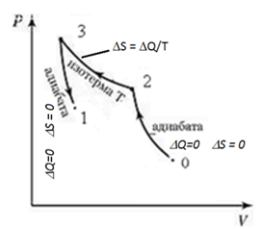

S- S0=S=== Q23/T=A23/T

47. Закон неубывания энтpопии изолиpованной системы. Формула Больцмана. Статистическое толкование втоpого начала теpмодинамики.

 Закон – в изолированной системе энтропия не уменьшается. Если в некоторый момент времени замкнутая система находится в неравновесном макроскопическом состоянии, то в последующие моменты времени наиболее вероятным следствием будет монотонное возрастание её энтропии.

Формула Больцмана: S=k*ln(P), k = R/N = 1,38*10-23 Дж/К,

где k - фундаментальная мировая постоянная Больцмана; R = 8,31 Дж/(моль*К) - молярная газовая постоянная; N = 6,06*1023 моль-1 - число Авогадро; Р - статистический вес: число способов осуществления данного состояния.

Параметр S - энтропия - служит мерой рассеяния энергии Вселенной, а Р - характеризует любые самопроизвольные изменения, эта величина относится к миру атомов, определяющих скрытый механизм изменения. Итак, формула, вывод которой дан отдельно, связывает энтропию с хаосом.

Утверждение второго закона (начала) термодинамики о невозможности убывания энтропии в изолированной системе может быть истолковано статически, на основе молекулярно-кинетической теории строения вещества, с помощью формулы Больцмана

48. Отклонение от законов идеальных газов. Реальные газы.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева. Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона: . p — давление; V - объем T — температура; Zr = Zr (p,T)  — коэффициент сжимаемости газа; m – масса; М — молярная масса; R — газовая постоянная.