Глава 2. Кривые и поверхности 2-го порядка.

I. Методические указания и примеры

§1. Кривые 2-го порядка.

Рассмотрим кривые, которые в некоторой подходящей прямоугольной декартовой системе координат определяются уравнениями вида:

, (1.1)

, (1.2)

. (1.3)

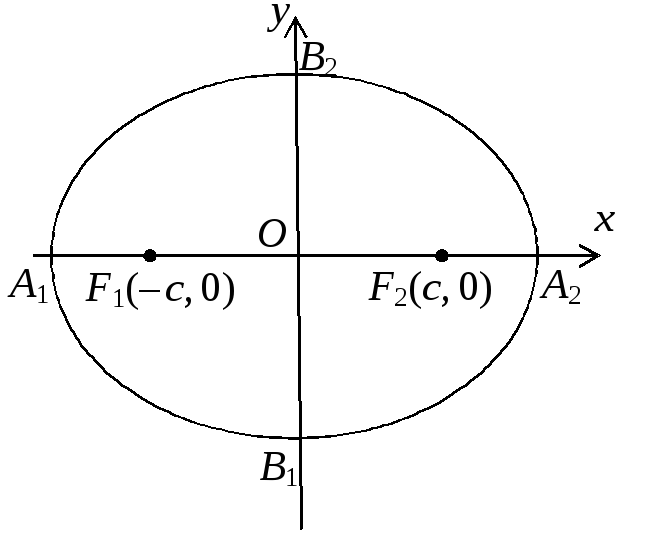
Рис. 1.1. Эллипс, А₁А₂ – большая ось,

В₁В₂ – малая ось, точки и – фокусы

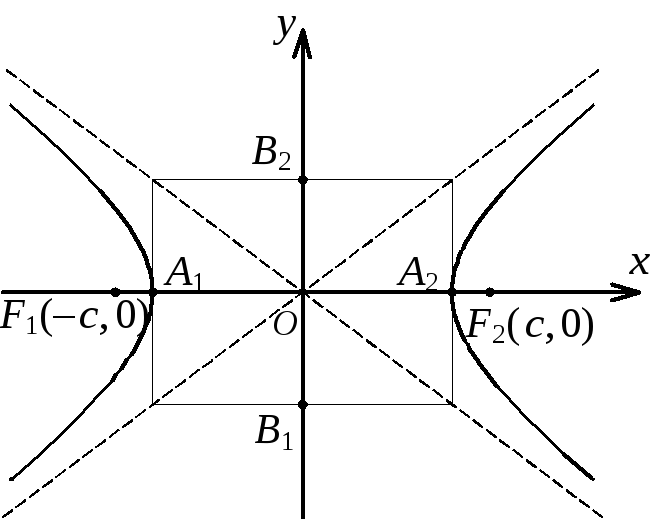
Рис. 1.2. Гипербола, А₁А₂ – действительная

ось гиперболы, точки и – фокусы

Эти кривые называются эллипсом, гиперболой и параболой соответственно. Уравнения (1.1) – (1.3) называются каноническими уравнениями этих кривых, а упомянутая система координат – канонической по отношению к данной кривой. В совокупности эллипс, гипербола и парабола называются невырожденными кривыми 2-го порядка (или кривыми 2-го порядка) в связи с тем, что они опре-

д

Рис. 1.3. Парабола, р – её параметр, точка F – фокус,

D– директриса

еляются уравнениями второй степени относительно координат. Заметим, что уравнение второй степени может задавать и другие линии (см., например, [1]).

На рисунках 1.1 – 1.3 изображены эллипс, гипербола и парабола, определяемые каноническими уравнениями (1.1) – (1.3), на рисунках 1.1, 1.2 точки А₁, А₂, В₁, В₂ имеют следующие координаты: А₁(– а, 0), А₂(а, 0), В₁(0, –b), В₂(0, b). На рисунке 1.2 пунктиром изображены асимптоты гиперболы, которые имеют уравнения: .

Для эллипса и гиперболы вводится понятие эксцентриситета е, определяемого формулой: , где для эллипса и для гиперболы. Эксцентриситет эллипса характеризует степень его сжатия к большой оси, а эксцентриситет гиперболы – степень её сжатия к действительной оси.

Пример 1.1. Написать уравнение прямой L, проходящей через фокус параболы параллельно прямой, проходящей через центр окружности

и левый фокус гиперболы .

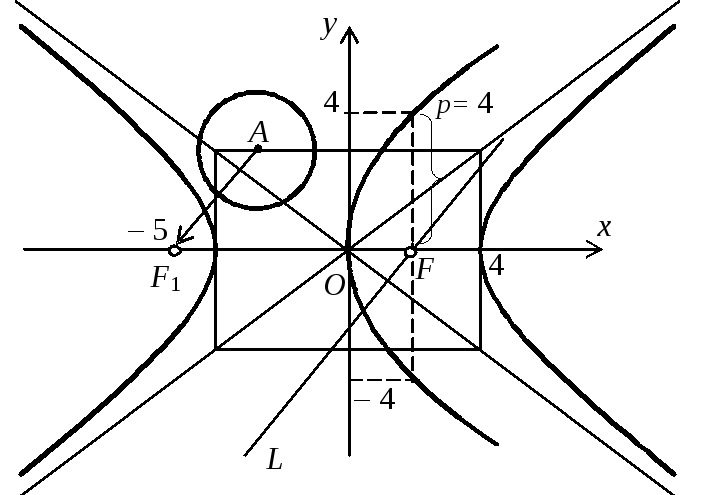Рис. 1.4. К примеру 1.1

►Сравнив уравнение данной параболы с уравнением (1.3), устанавливаем, что 2р = 8, р = 4. Фокус параболы, определяемой уравнением (1.3), находится в точке (р/2, 0), поэтому точка F(2, 0) – фокус данной параболы (рис. 1.4). В уравнении окружности выделим полные квадраты из членов, содержащих координаты, т. е. преобразуем его к виду: , откуда получаем: . Таким образом, точка А(–3, 3) – центр данной окружности (рис. 1.4). Левый фокус гиперболы, определяемой уравнением (1.2), находится в точке (– с, 0), при этом . Так как а = 4, а b = 3, то с = 5, поэтому точка F₁(–5, 0) – левый фокус заданной гиперболы (рис. 1.4). Напишем каноническое уравнение прямой L, т.е. уравнение вида:

, (1.4)

где – координаты любой точки , принадлежащей данной прямой, а – координаты любого вектора , параллельного данной прямой (называемого её направляющим вектором). За точку в данном случае примем точку F(2, 0), а за вектор – вектор . Подставив координаты точки F и вектора в уравнение (1.4), имеем: L: или L: .◄

Пример 1.2. Написать уравнение и найти длину перпендикуляра, опущенного из начала координат на прямую, проходящую через центр окружности и фокус параболы .

►В уравнении окружности выделим полные квадраты из членов, содержащих координаты, т. е. преобразуем его к виду: , откуда получаем: . Таким образом, точка А(2, 0) – центр данной окружности, а её радиус равен 2 (рис. 1.5). Сравним уравнение данной параболы с каноническим уравнением вида: . Осью симметрии такой параболы является ось Оу, ветви её направлены вниз, а фокус находится в точке (0, –р/2). В данном случае 2р = 4, р = 2, а точка F(0, –1) – фокус (рис. 1.5). Подставим в (1.4) координаты точки А и вектора : . После очевидных преобразований имеем: (FA): . Длину перпендикуляра (ОВ) вычислим, по формуле для расстояния d от точки до прямой L: ,

Рис. 1.5. К примеру 1.2

. (1.5)

Подставив в (1.5) координаты точки О(0, 0) и коэффициенты уравнения прямой (FA), получим: |ОВ| =. Для прямой (ОВ) – вектор нормали. Подставив его координаты и координаты точки О(0,0) в уравнение , имеем (ОВ): или (ОВ): .◄