Проверка на наличие основной тенденции

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет управления

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЛР1 Журавлева М.docx

Скачиваний:

Добавлен:

18.07.2019

Размер:

1.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

Проверка на наличие основной тенденции

А) Графический анализ

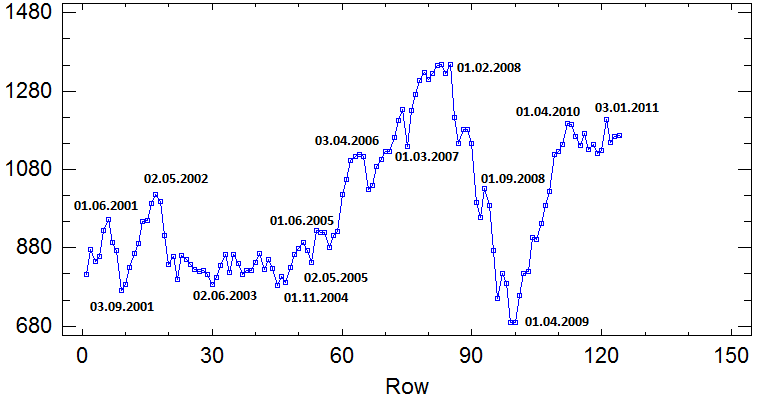
Рисунок 1

По графику видно, что наблюдается рост показателя, а также циклическая составляющая, связанная с изменением экономической ситуации. Также возможно наличие сезонной составляющей.

Б) Проверка гипотез о наличии тенденции

Разделим данные на две выборки по 62 значения. В приложении 7 осуществлена проверка гипотез о равенстве средних, дисперсий двух нормально распределенных совокупностей. Средние двух совокупностей не равны, что говорит о наличии тренда.

В) Анализ абсолютных приростов

Посчитаем абсолютные цепные приросты по формуле:

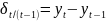
А также выделим периоды роста, спада и относительной стабильности показателя и посчитаем абсолютный прирост за эти периоды. Жирным шрифтом выделены аномальные для данного периода значения, возможно связанные с сезонностью.

В начале наблюдается 2 периода роста и 2 периода спада, которые являются относительно равномерными. На фазе стабильности происходит постоянная смена небольших подъемов и спадов. Абсолютный прирост на этой фазе составил +4,21.

Далее следует фаза резкого подъема. Если объединить ее с фазой стабильности, то можно сказать о наличии роста с ускорением. Стоит отметить, что каждый девятый месяц на подъеме можно наблюдать значительный спад.

Следующая фаза - резкий спад. Причем примерно каждый четвертый месяц на спаде можно наблюдать подъем показателя.

За спадом следует резкий подъем. Нетипичное поведение показателя на данном подъеме наблюдается каждый пятый месяц.

Следующая фаза – достаточно плавный спад.

Последняя фаза - рост сначала с ускорением, потом с замедлением.

AEX CONSUMER GOODS
№	Date	closing	Абсолютный прирост (цепной)	Абсолютный прирост (цепной) по периоду
1	02.01.2001	813,17		Рост
2	01.02.2001	877,02	63,85	140,01
3	01.03.2001	844,36	-32,66
4	02.04.2001	856,69	12,33
5	01.05.2001	924,97	68,28
6	01.06.2001	953,18	28,21
7	02.07.2001	892,74	-60,44	Спад
8	01.08.2001	874,46	-18,28	-181,78
9	03.09.2001	771,4	-103,06	-181,78
10	01.10.2001	785,72	14,32	Рост
11	01.11.2001	829,36	43,64	245,96
12	03.12.2001	865,08	35,72
13	02.01.2002	892,15	27,07
14	01.02.2002	947,28	55,13
15	01.03.2002	948,6	1,32
16	02.04.2002	992,79	44,19
17	02.05.2002	1017,36	24,57
18	03.06.2002	997,49	-19,87	Спад
19	01.07.2002	911,97	-85,52	-180,15
20	01.08.2002	837,21	-74,76	-180,15
21	02.09.2002	857,42	20,21	Стабильность
22	01.10.2002	798,01	-59,41	4,21
23	01.11.2002	859,33	61,32
24	02.12.2002	849,27	-10,06
25	02.01.2003	838,65	-10,62
26	03.02.2003	824,31	-14,34
27	03.03.2003	820,56	-3,75
28	01.04.2003	821,28	0,72
29	02.05.2003	812,44	-8,84
30	02.06.2003	786,55	-25,89
31	01.07.2003	804,84	18,29
32	01.08.2003	834,95	30,11
33	01.09.2003	863,61	28,66
34	01.10.2003	816,88	-46,73
35	03.11.2003	862,39	45,51
36	01.12.2003	839,67	-22,72
37	02.01.2004	812,22	-27,45
38	02.02.2004	822,04	9,82
39	01.03.2004	823,26	1,22
40	01.04.2004	843,39	20,13
41	03.05.2004	865,42	22,03
42	01.06.2004	825,66	-39,76
43	01.07.2004	850,26	24,6
44	02.08.2004	828,34	-21,92
45	01.09.2004	783,02	-45,32
46	01.10.2004	807,71	24,69
47	01.11.2004	791,73	-15,98
48	01.12.2004	829,32	37,59
49	03.01.2005	863,65	34,33
50	01.02.2005	878,19	14,54
51	01.03.2005	894,68	16,49
52	01.04.2005	873,43	-21,25
53	02.05.2005	841,42	-32,01
54	01.06.2005	923,94	82,52	Рост
55	01.07.2005	919,01	-4,93	506,3
56	01.08.2005	919,19	0,18
57	01.09.2005	881,18	-38,01
58	03.10.2005	911,06	29,88
59	01.11.2005	921,6	10,54
60	01.12.2005	1016,39	94,79
61	02.01.2006	1055,37	38,98
62	01.02.2006	1103,51	48,14
63	01.03.2006	1112,47	8,96
64	03.04.2006	1119,03	6,56
65	02.05.2006	1113,04	-5,99
66	01.06.2006	1028,2	-84,84
67	03.07.2006	1038,78	10,58
68	01.08.2006	1086,43	47,65
69	01.09.2006	1105,96	19,53
70	02.10.2006	1125,8	19,84
71	01.11.2006	1124,88	-0,92
72	01.12.2006	1162,68	37,8
73	02.01.2007	1204,92	42,24
74	01.02.2007	1232,24	27,32
75	01.03.2007	1138,69	-93,55
76	02.04.2007	1230,79	92,1
77	02.05.2007	1271,72	40,93
78	01.06.2007	1307,78	36,06
79	02.07.2007	1328,18	20,4
80	01.08.2007	1310,47	-17,71
81	03.09.2007	1326,15	15,68
82	01.10.2007	1344,56	18,41
83	01.11.2007	1348,83	4,27
84	03.12.2007	1324,74	-24,09
85	02.01.2008	1347,72	22,98
86	01.02.2008	1213,49	-134,23	Спад
87	03.03.2008	1145,62	-67,87	-657,87
88	01.04.2008	1180,98	35,36
89	02.05.2008	1181,07	0,09
90	02.06.2008	1145,27	-35,8
91	01.07.2008	995,52	-149,75
92	01.08.2008	957,73	-37,79
93	01.09.2008	1030,47	72,74
94	01.10.2008	987,7	-42,77
95	03.11.2008	874,21	-113,49
96	01.12.2008	749,78	-124,43
97	02.01.2009	815,25	65,47
98	02.02.2009	788,89	-26,36
99	02.03.2009	688,15	-100,74
100	01.04.2009	689,85	1,7
101	04.05.2009	758,83	68,98	Рост
102	01.06.2009	813,63	54,8	506,6
103	01.07.2009	820,49	6,86
104	03.08.2009	906,61	86,12
105	01.09.2009	902,04	-4,57
106	01.10.2009	941,57	39,53
107	02.11.2009	988,37	46,8
108	01.12.2009	1024,29	35,92
109	04.01.2010	1117,68	93,39
110	01.02.2010	1125,11	7,43
111	01.03.2010	1142,6	17,49
112	01.04.2010	1196,45	53,85
113	03.05.2010	1193,84	-2,61	Спад
114	01.06.2010	1163,26	-30,58	-76,37
115	01.07.2010	1141,02	-22,24
116	02.08.2010	1170,72	29,7
117	01.09.2010	1132,32	-38,4
118	01.10.2010	1143,91	11,59
119	01.11.2010	1120,08	-23,83
120	01.12.2010	1128,26	8,18	Рост
121	03.01.2011	1207,35	79,09	46,88
122	01.02.2011	1148,54	-58,81
123	01.03.2011	1163,89	15,35
124	01.04.2011	1166,96	3,07

Таблица 10

Исходя из вышесказанного, можно сделать вывод, что наблюдается рост с качественными изменениями динамических характеристик. Поэтому целесообразно использовать следующие модели:

Линейно-логарифмическая функция 2-го порядка:
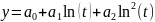
Парабола третьего порядка:
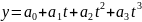
Логистическая функция: 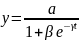, где
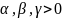
Первая функция Торнквиста: 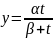, где
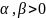
Кривая Гомперца: 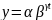, где

Также рассмотрим модель линейного тренда.

Выбор модели

Модели были построены в приложении 8, а спрогнозированные значения представлены в таблице 11. Все коэффициенты моделей и модели в целом значимы с вероятностью 95%. Для определения прогностических характеристик выведем остатки моделей (приложение 9).

Прогностические и информационные характеристики представлены в таблице 12.

период	значение показателя	Модель тренда
период	значение показателя	линейного тренда	Линейно-логарифмическая функция 2-го порядка	Парабола третьего порядка	Логистическая функция	Первая функция Торнквиста	Кривая Гомперца
вид модели		Y = a + b* t	Y = a + b* log(t)+c*log^2(t)	Y = a + b* t^2+c*t^3	Y = a/(1+be^(-ct))	Y = a*t/(b+t)	Y = ab^(ct)
вид модели		Y = 824,41 + 2,52608*t	Y= 951,229 - 136,183log(t) + 17,70582*log(t)^2	Y = 829,366 + 0,0739677t^2 - 0,000476454t^3	Y= 1237,61/(1+0.55exp(-0.013*t))	Y = 1012,93*t/(0.85+t)	Y= 832,0811.09^(0.03t)
1	813,17	826,936	951,229	829,439	802,06	547,53	834,235
2	877,02	829,463	873,848	829,658	805,722	710,828	836,395
3	844,36	831,989	844,357	830,018	809,369	789,296	838,56
4	856,69	834,515	830,494	830,519	813,002	835,406	840,731
5	924,97	837,041	823,778	831,155	816,62	865,752	842,907
6	953,18	839,567	820,908	831,926	820,223	887,238	845,089
7	892,74	842,093	820,318	832,827	823,811	903,25	847,277
8	874,46	844,619	821,168	833,856	827,383	915,643	849,47
9	771,4	847,145	822,965	835,01	830,94	925,52	851,669
10	785,72	849,671	825,406	836,286	834,481	933,576	853,874
11	829,36	852,197	828,29	837,682	838,006	940,273	856,084
12	865,08	854,723	831,486	839,194	841,515	945,927	858,3
13	892,15	857,249	834,899	840,819	845,007	950,765	860,522
14	947,28	859,776	838,464	842,556	848,483	954,951	862,75
15	948,6	862,302	842,132	844,4	851,942	958,609	864,983
16	992,79	864,828	845,868	846,35	855,384	961,833	867,222
17	1017,36	867,354	849,647	848,401	858,809	964,695	869,467
18	997,49	869,88	853,448	850,552	862,217	967,254	871,718
19	911,97	872,406	857,256	852,8	865,607	969,555	873,975
20	837,21	874,932	861,06	855,141	868,98	971,635	876,237
21	857,42	877,458	864,852	857,573	872,335	973,525	878,505
22	798,01	879,984	868,624	860,093	875,673	975,25	880,78
23	859,33	882,51	872,372	862,697	878,992	976,83	883,06
24	849,27	885,036	876,091	865,384	882,293	978,282	885,346
25	838,65	887,562	879,779	868,151	885,576	979,623	887,637
26	824,31	890,088	883,434	870,994	888,841	980,863	889,935
27	820,56	892,615	887,053	873,91	892,087	982,015	892,239
28	821,28	895,141	890,636	876,897	895,315	983,086	894,549
29	812,44	897,667	894,182	879,952	898,524	984,086	896,864
30	786,55	900,193	897,691	883,072	901,714	985,021	899,186
31	804,84	902,719	901,162	886,254	904,885	985,897	901,514
32	834,95	905,245	904,596	889,496	908,038	986,72	903,847
33	863,61	907,771	907,992	892,794	911,171	987,494	906,187
34	816,88	910,297	911,351	896,146	914,285	988,224	908,533
35	862,39	912,823	914,672	899,548	917,379	988,913	910,885
36	839,67	915,349	917,958	902,998	920,455	989,565	913,243
37	812,22	917,875	921,207	906,494	923,511	990,182	915,607
38	822,04	920,401	924,42	910,031	926,547	990,768	917,977
39	823,26	922,928	927,599	913,608	929,564	991,324	920,354
40	843,39	925,454	930,742	917,221	932,561	991,853	922,736
41	865,42	927,98	933,853	920,868	935,538	992,357	925,125
42	825,66	930,506	936,929	924,545	938,496	992,837	927,52
43	850,26	933,032	939,973	928,25	941,434	993,295	929,921
44	828,34	935,558	942,985	931,981	944,352	993,733	932,328
45	783,02	938,084	945,966	935,733	947,25	994,152	934,741
46	807,71	940,61	948,915	939,505	950,128	994,552	937,161
47	791,73	943,136	951,834	943,293	952,987	994,936	939,587
48	829,32	945,662	954,724	947,095	955,825	995,305	942,019
49	863,65	948,188	957,584	950,908	958,643	995,658	944,458
50	878,19	950,714	960,416	954,728	961,441	995,998	946,903
51	894,68	953,24	963,219	958,553	964,22	996,325	949,354
52	873,43	955,767	965,995	962,381	966,978	996,639	951,812
53	841,42	958,293	968,745	966,208	969,716	996,941	954,276
54	923,94	960,819	971,467	970,031	972,433	997,233	956,746
55	919,01	963,345	974,164	973,848	975,131	997,514	959,223
56	919,19	965,871	976,836	977,655	977,809	997,785	961,706
57	881,18	968,397	979,483	981,451	980,466	998,047	964,195
58	911,06	970,923	982,105	985,231	983,103	998,3	966,691
59	921,6	973,449	984,703	988,993	985,721	998,544	969,194
60	1016,39	975,975	987,278	992,735	988,318	998,781	971,703
61	1055,37	978,501	989,83	996,453	990,895	999,009	974,218
62	1103,51	981,027	992,359	1000,14	993,452	999,231	976,74
63	1112,47	983,553	994,866	1003,81	995,988	999,445	979,269
64	1119,03	986,08	997,351	1007,44	998,505	999,653	981,804
65	1113,04	988,606	999,815	1011,03	1001	999,855	984,345
66	1028,2	991,132	1002,26	1014,59	1003,48	1000,05	986,893
67	1038,78	993,658	1004,68	1018,11	1005,94	1000,24	989,448
68	1086,43	996,184	1007,08	1021,58	1008,37	1000,42	992,009
69	1105,96	998,71	1009,46	1025,01	1010,79	1000,6	994,577
70	1125,8	1001,24	1011,83	1028,38	1013,19	1000,78	997,152
71	1124,88	1003,76	1014,17	1031,71	1015,57	1000,95	999,733
72	1162,68	1006,29	1016,49	1034,98	1017,92	1001,11	1002,32
73	1204,92	1008,81	1018,8	1038,19	1020,26	1001,27	1004,92
74	1232,24	1011,34	1021,09	1041,34	1022,58	1001,43	1007,52
75	1138,69	1013,87	1023,36	1044,43	1024,88	1001,58	1010,13
76	1230,79	1016,39	1025,61	1047,45	1027,16	1001,73	1012,74
77	1271,72	1018,92	1027,85	1050,4	1029,42	1001,87	1015,36
78	1307,78	1021,44	1030,06	1053,28	1031,66	1002,01	1017,99
79	1328,18	1023,97	1032,27	1056,09	1033,88	1002,15	1020,63
80	1310,47	1026,5	1034,45	1058,81	1036,08	1002,28	1023,27
81	1326,15	1029,02	1036,62	1061,46	1038,26	1002,41	1025,92
82	1344,56	1031,55	1038,77	1064,02	1040,43	1002,54	1028,57
83	1348,83	1034,08	1040,91	1066,5	1042,57	1002,66	1031,24
84	1324,74	1036,6	1043,03	1068,89	1044,7	1002,78	1033,9
85	1347,72	1039,13	1045,14	1071,18	1046,8	1002,9	1036,58
86	1213,49	1041,65	1047,23	1073,38	1048,89	1003,02	1039,26
87	1145,62	1044,18	1049,31	1075,48	1050,96	1003,13	1041,95
88	1180,98	1046,71	1051,37	1077,48	1053,01	1003,24	1044,65
89	1181,07	1049,23	1053,42	1079,38	1055,04	1003,35	1047,36
90	1145,27	1051,76	1055,46	1081,17	1057,05	1003,45	1050,07
91	995,52	1054,28	1057,48	1082,85	1059,05	1003,56	1052,79
92	957,73	1056,81	1059,49	1084,42	1061,03	1003,66	1055,51
93	1030,47	1059,34	1061,48	1085,87	1062,98	1003,76	1058,24
94	987,7	1061,86	1063,46	1087,21	1064,92	1003,85	1060,98
95	874,21	1064,39	1065,43	1088,42	1066,84	1003,95	1063,73
96	749,78	1066,91	1067,38	1089,52	1068,75	1004,04	1066,48
97	815,25	1069,44	1069,33	1090,48	1070,63	1004,13	1069,24
98	788,89	1071,97	1071,26	1091,32	1072,5	1004,22	1072,01
99	688,15	1074,49	1073,17	1092,02	1074,35	1004,31	1074,79
100	689,85	1077,02	1075,08	1092,59	1076,18	1004,39	1077,57
101	758,83	1079,54	1076,97	1093,02	1078	1004,48	1080,36
102	813,63	1082,07	1078,85	1093,31	1079,8	1004,56	1083,16
103	820,49	1084,6	1080,73	1093,45	1081,58	1004,64	1085,96
104	906,61	1087,12	1082,58	1093,45	1083,34	1004,72	1088,77
105	902,04	1089,65	1084,43	1093,3	1085,09	1004,8	1091,59
106	941,57	1092,17	1086,27	1093	1086,81	1004,87	1094,41
107	988,37	1094,7	1088,09	1092,54	1088,53	1004,95	1097,25
108	1024,29	1097,23	1089,91	1091,93	1090,22	1005,02	1100,09
109	1117,68	1099,75	1091,71	1091,15	1091,9	1005,09	1102,94
110	1125,11	1102,28	1093,51	1090,21	1093,56	1005,16	1105,79
111	1142,6	1104,81	1095,29	1089,11	1095,21	1005,23	1108,65
112	1196,45	1107,33	1097,06	1087,83	1096,84	1005,3	1111,52
113	1193,84	1109,86	1098,83	1086,38	1098,45	1005,37	1114,4
114	1163,26	1112,38	1100,58	1084,76	1100,04	1005,43	1117,29
115	1141,02	1114,91	1102,32	1082,96	1101,62	1005,5	1120,18
116	1170,72	1117,44	1104,05	1080,98	1103,19	1005,56	1123,08
117	1132,32	1119,96	1105,78	1078,81	1104,74	1005,62	1125,99
118	1143,91	1122,49	1107,49	1076,46	1106,27	1005,69	1128,9
119	1120,08	1125,01	1109,2	1073,92	1107,79	1005,75	1131,82
120	1128,26	1127,54	1110,89	1071,19	1109,29	1005,81	1134,75
121	1207,35	1130,07	1112,58	1068,26	1110,78	1005,86	1137,69
122	1148,54	1132,59	1114,26	1065,13	1112,25	1005,92	1140,64
123	1163,89	1135,12	1115,92	1061,8	1113,7	1005,98	1143,59
124	1166,96	1137,64	1117,58	1058,27	1115,14	1006,03	1146,55
125	1156,66	1140,17	1119,23	1054,54	1116,57	1006,09	1149,52
126	1155,66	1142,69608	1120,87	1050,59	1117,98	1006,14	1152,49
127	1134,28	1145,22216	1122,51	1046,43	1119,38	1006,2	1155,48
128	1104,87	1147,74824	1124,13	1042,05	1120,76	1006,25	1158,47
129	1055,55	1150,27432	1125,75	1037,46	1122,13	1006,3	1161,47
130		1152,8004	1127,36	1032,65	1123,48	1006,35	1164,47

Таблица 11

модель	Характеристики модели
модель	R^2	s^2	s	DW	Kt	Kt2	Ut
линейного тренда	28,4786	20869,27	144,462	0,110215 (P=0,0000)	0,022749	0,015921	0,011258
Линейно-логарифмическая функция 2-го порядка	27,4358	21001,52	144,919	0,117019 (P=0,0000)	0,029717	0,021009	0,014855
Парабола третьего порядка	31,4408	20170,25	142,022	0,115369 (P=0,0000)	0,084498	0,0618	0,043726
Логистическая функция	97,9494	20540,05	143,318	0,111105	0,031349	0,022194	0,015693
Первая функция Торнквиста	97,302	27025,72	164,395	0,0900128	0,124169	0,092443	0,065464
Кривая Гомперца	97,9222	20813,26	144,268	0,10961	0,02457	0,017116	0,012104

Таблица 12

Наилучшие прогностические характеристики (наименьшее значение коэффициентов Тейла) имеют модели линейного тренда и кривая Гомперца. Лучшие информационные характеристики имеют логистическая функция и кривая Гомперца. R^2 кривой Гомперца намного превосходит R^2 линейной функции, а также стандартная ошибка кривой Гомперца немного меньше, чем у модели линейного тренда. Поэтому целесообразно выбрать кривую Гомперца: (Y= 832,081*1.09^(0.03*t)). Стоит отметить значительный автокорреляционный эффект во всех моделях. Он может быть исправлен построением модели ARIMA для остатков.

Проанализируем зависимость точности прогноза от длительности ретроспективного периода, перестроив логистическую модель (приложение 10). Оценим прогностические и информационные характеристики полученных моделей:

n (n<=T)	модель	характеристика модели
n (n<=T)	модель	R^2	s	s^2	Kt	Kt2	Ut
124	Y= 832,0811.09^(0.03t)	97,9222	144,268	20813,26	0,048163483	0,03355294	0,023728
110	Y= 830,491.09^(0.03t)	97,7667	151,933	23083,64	0,046936954	0,03273072	0,023146
100	Y = 828,1551.09^(0.03t)	97,6608	157,046	24663,45	0,045238255	0,03159181	0,02234
90	Y = 833,7841.09^(0.03t)	97,5596	163,605	26766,6	0,049522289	0,03446327	0,024372
80	Y = 841,4421.09^(0.03t)	97,4645	170,525	29078,78	0,056217195	0,03893752	0,027539
60	Y = 852,0861.09^(0.03t)	97,1608	187,915	35312,05	0,066655808	0,04586481	0,032443
40	Y = 790,1031.09^(0.03t)	97,6248	163,672	26788,52	0,043003566	0,03074668	0,021743
30	Y =761,0611.09^(0.03t)	97,7766	155,001	24025,31	0,068435405	0,04981643	0,035241
20	Y = 830,3431.09^(0.03t)	99,58	73,647	5423,881	0,046829181	0,03265856	0,023095

Таблица 13

Из таблицы 13 видно, что лучшими прогностическими характеристиками обладает модель, построенная по последним 40 наблюдениям.

Построим доверительный интервал по формуле:

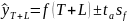
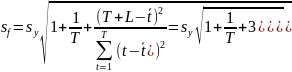
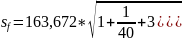
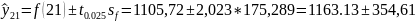
Значение индекса в 130 периоде находится в интервалах от 808,52 до 1517,74.

Этап 4. Сглаживание временного ряда с использованием авторегрессионной модели. Оценка точности прогнозирования уровня показателя.

По графику ACF в приложении 11 можно предположить наличие автокорреляции 7-го порядка. Проверим эту гипотезу, используя критерий Бокса-Пирса и Бокса-Льюинга.

Н0: значения временного ряда не являются автокоррелированными с порядком автокорреляции до 7 включительно.

Критерий Бокса-Пирса:

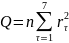
Критерий Бокса-Льюинга:

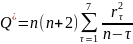
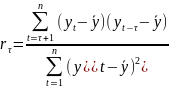
В приложении 12 были посчитаны значения r, суммы r^2 и суммы r^2/(122). Таким образом:

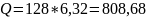
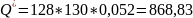
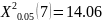
Каждая из расчетных статистик больше критического значения, поэтому первые 7 значений ACF не могут игнорироваться и быть признаны несущественными.

Рассчитаем статистики для 7-го значения ACF:

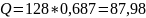
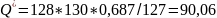
Каждая из расчетных статистик больше критического значения, поэтому 7-е значение ACF не может игнорироваться и быть признано несущественными.

Из этого можно сделать вывод о наличии автокорреляции7-го или большего порядка.

По графикам автокорреляции и частной корреляции в приложении 11 можно сделать вывод о наличии смешанного процесса, так как функции ACF и PACF бесконечны. Так как дисперсии и средние двух частей выборки не равны, то следует проинтегрировать (использовать разности d-го порядка). Интегрирование применяется для того, чтобы привести ряд к стационарному виду.

Рассмотрим разности 1го, 2го, 3го и 4го порядка:

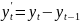
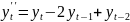
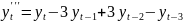
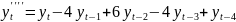
Посчитаем разности и проверим гипотезы о равенстве дисперсий и средних (приложение 13). Для разностей первого и второго порядка наблюдается неравенство дисперсий двух выборок. То есть эти ряды не являются стационарными. Дисперсии и средние рядов разностей третьего и четвертого порядка равны, то есть ряды стационарны. Значит, для построения модели ARIMA следует использовать порядок интегрирования 3 или 4.

В приложении 13 было построено несколько моделей ARIMA(p,d,q). Параметры подбирались по следующим критериям:

Значимость всех коэффициентов
Модели должны пройти тесты на случайность (Test for excessive runs up and down и Test for excessive runs above and below median), тест на автокорреляцию Бокса-Пирса и на различия в дисперсиях и средних (приложение 12 п.6)

В таблице 14 представлены спрогнозированные значения по моделям:

период	значение показателя	Авторегрессионные модели
период	значение показателя	ARIMA(4,3,1)	ARIMA(3,3,1)	ARIMA(3,4,2)	ARIMA(4,4,2)	ARIMA(4,4,1)
1	813,17
2	877,02
3	844,36
4	856,69	863,788	862,796
5	924,97	885,396	874,361	873,225	868,973	845,132
6	953,18	956,914	940,153	955,204	951,514	950,767
7	892,74	964,292	942,684	960,869	959,697	974,068
8	874,46	876,158	875,847	885,377	843,561	840,333
9	771,4	880,65	867,038	870,724	857,13	856,977
10	785,72	748,872	711,211	698,039	713,65	679,511
11	829,36	757,653	730,027	727,636	721,56	702,891
12	865,08	790,248	795,106	810,112	779,551	827,312
13	892,15	836,335	831,049	859,764	855,134	929,409
14	947,28	875,169	899,032	935,248	896,399	935,91
15	948,6	974,106	969,458	1007,62	1022,97	1056,59
16	992,79	969,05	953,726	984,179	1002,02	976,765
17	1017,36	1019,9	1006,75	1037,74	1040,27	1013,53
18	997,49	1038,82	1028,82	1056,96	1053,95	1042,39
19	911,97	1007,64	984,228	1004,12	1008,4	990,719
20	837,21	896,604	881,422	885,643	864,352	822,04
21	857,42	817,276	784,165	776,664	777,594	743,186
22	798,01	832,038	806,541	808,613	805,268	797,202
23	859,33	733,88	717,386	721,656	707,424	731,469
24	849,27	820,41	829,068	854,995	817,544	871,541
25	838,65	817,118	827,972	856,07	839,628	898,911
26	824,31	826,515	807,456	834,413	853,448	866,887
27	820,56	809,657	815,475	839,627	819,963	797,322
28	821,28	821,069	791,13	811,74	842,95	839,375
29	812,44	803,988	793,836	816,387	808,26	784,024
30	786,55	794,107	783,851	806,614	799,395	807,083
31	804,84	766,149	755,731	775,62	767,297	766,584
32	834,95	795,996	784,633	808,077	804,808	808,47
33	863,61	828,116	818,08	846,741	846,449	859,557
34	816,88	858,382	852,282	885,754	879,308	895,829
35	862,39	803,124	798,943	823,192	809,018	805,942
36	839,67	879,335	865,607	892,902	895,621	890,657
37	812,22	836,913	818,153	838,254	846,638	832,219
38	822,04	799,014	775,053	791,506	791,296	771,051
39	823,26	809,789	810,777	829,942	800,853	797,292
40	843,39	817,395	791,574	810,39	827,295	846,564
41	865,42	828,779	823,056	848,013	831,224	831,739
42	825,66	860,085	858,744	887,232	873,628	899,236
43	850,26	816,855	801,467	821,572	824,582	824,871
44	828,34	855,058	843,603	865,855	860,95	847,237
45	783,02	821,624	803,693	820,491	826,417	819,89
46	807,71	762,627	738,382	749,649	751,093	731,878
47	791,73	794,642	792,122	809,987	787,227	786,813
48	829,32	775,056	753,513	770,056	782,399	803,033
49	863,65	816,287	809,665	836,075	823,57	832,765
50	878,19	859,462	864,729	896,627	880,428	911,599
51	894,68	886,522	871,266	902,072	914,999	931,989
52	873,43	904,945	902,221	931,628	921,193	907,676
53	841,42	884,695	864,123	884,076	895,705	881,221
54	923,94	841,3	817,232	829,112	832,861	795,754
55	919,01	938,768	926,113	950,223	945,294	946,374
56	919,19	910,693	896,217	919,42	920,19	941,175
57	881,18	912,983	906,962	931,116	911,13	917,009
58	911,06	878,387	875,851	890,427	873,13	868,926
59	921,6	929,349	893,894	909,225	940,167	932,831
60	1016,39	911,98	901,677	920,07	909,75	895,418
61	1055,37	1028,82	1022,42	1056,78	1050,02	1089,7
62	1103,51	1065,93	1074,34	1111,87	1093,67	1128,85
63	1112,47	1139,99	1129,47	1166,71	1174,33	1191,41
64	1119,03	1147,76	1142,74	1170,87	1165,98	1141,78
65	1113,04	1159,71	1126,67	1145,12	1170,29	1139,2
66	1028,2	1131,07	1110,78	1122,73	1117,29	1073,07
67	1038,78	1017,91	986,315	982,926	982,719	951,898
68	1086,43	1031,61	1011,44	1012,54	997,119	980,949
69	1105,96	1077,55	1063,18	1075,77	1071,77	1105,27
70	1125,8	1086,22	1074,87	1096,42	1090,15	1132,19
71	1124,88	1115,35	1129,99	1157,35	1121,03	1154,31
72	1162,68	1139,82	1128,56	1150,33	1162,07	1182,67
73	1204,92	1187,6	1166,28	1188,75	1208,87	1190,38
74	1232,24	1222,91	1211,16	1236,74	1239,81	1231,09
75	1138,69	1248,61	1236,32	1262,72	1263,08	1268,52
76	1230,79	1130,75	1116,62	1124,4	1114,42	1087,2
77	1271,72	1266,26	1246,84	1265,03	1269,77	1259,52
78	1307,78	1285,21	1267,65	1289,22	1302,35	1315,12
79	1328,18	1313,29	1296,36	1324,8	1322,64	1339,46
80	1310,47	1338,08	1360,39	1389,07	1340,02	1354,5
81	1326,15	1344,82	1310,81	1326,28	1362,92	1368,69
82	1344,56	1347,66	1326,25	1339,38	1342,16	1291,9
83	1348,83	1357,03	1336,93	1350,38	1352,38	1345,45
84	1324,74	1349,85	1332,21	1346,38	1341,77	1344,73
85	1347,72	1317,23	1308,73	1319,5	1301,66	1302,93
86	1213,49	1356,26	1339,98	1353,21	1354,28	1363,4
87	1145,62	1180,12	1152,95	1145,78	1150,25	1121,55
88	1180,98	1112,62	1083,77	1071,72	1065,98	1026,46
89	1181,07	1154,59	1141,62	1142,69	1136,94	1148,69
90	1145,27	1136,97	1109,43	1121,38	1141,65	1187,98
91	995,52	1084,59	1101,75	1120,84	1072,43	1100,04
92	957,73	943,826	937,157	935,803	928,758	939,111
93	1030,47	935,09	898,014	893,537	927,136	888,658
94	987,7	1003,57	984,762	1000,36	1017,69	1017,06
95	874,21	922,364	910,008	931,582	932,666	971,073
96	749,78	802,609	818,469	832,635	783,467	791,346
97	815,25	708,454	690,737	686,279	696,162	679,256
98	788,89	803,932	760,414	770,778	822,892	800,797
99	688,15	719,292	708,036	727,686	726,024	733,232
100	689,85	606,201	609,098	626,854	592,652	618,859
101	758,83	657,899	673,31	696,022	667,649	691,122
102	813,63	763,592	731,967	764,369	822,538	853,129
103	820,49	794,661	790,712	836,718	838,411	841,854
104	906,61	808,968	828,863	875,897	842,693	869,08
105	902,04	952,964	951,392	1001,4	1012,37	1033,32
106	941,57	938,544	915,108	951,417	982,419	949,647
107	988,37	979,04	956,934	990,796	997,315	950,612
108	1024,29	1023,24	1018,3	1050,73	1036,12	1019,88
109	1117,68	1061,89	1032,14	1061,63	1079,22	1079,46
110	1125,11	1157,2	1157,81	1195,94	1169,65	1167,71
111	1142,6	1160,49	1146,97	1176,35	1174,87	1189,74
112	1196,45	1182,91	1164,13	1187,05	1182,38	1159,96
113	1193,84	1243,21	1230,52	1252,23	1244,99	1230,6
114	1163,26	1224,08	1189,96	1203,66	1221,11	1209,64
115	1141,02	1168,73	1153,72	1160,46	1136,38	1105,74
116	1170,72	1148,45	1129,35	1129,95	1118,97	1112,53
117	1132,32	1180,66	1151,88	1156,97	1166,7	1169,87
118	1143,91	1109,2	1092,72	1096,06	1084,58	1087,08
119	1120,08	1131,51	1124,06	1133,88	1114,61	1135,29
120	1128,26	1107,12	1098,48	1105,95	1100,67	1118,94
121	1207,35	1124,71	1100,3	1110,86	1126,91	1133,41
122	1148,54	1212,24	1214,64	1240,01	1227,18	1245,71
123	1163,89	1135,86	1118,96	1134,37	1146,54	1164,69
124	1166,96	1169,89	1163,21	1180,64	1168,97	1152,26
125	1156,66	1178,58	1166,03	1179,55	1188,62	1185,92
126	1155,66	1159,38	1121,26	1132,29	1164,36	1149,16
127	1134,28	1140,57	1142,67	1156,91	1125,4	1109,19
128	1104,87	1129,12	1109,4	1119,91	1128,69	1147,22
129	1055,55	1091	1072,22	1079,84	1080,83	1065,7
130		1031,56	1014,09	1016,97	1013,75	1001,46

Таблица 14

Посчитаем прогностические и информационные характеристики:

, где ,

	ARIMA(4,3,1)	ARIMA(3,3,1)	ARIMA(3,4,2)	ARIMA(4,4,2)	ARIMA(4,4,1)
SSer	297167,355	350748,418	364327,3543	362869,726	446664,03
s^2	2476,39463	2898,74725	3061,574406	3075,16717	3753,47924
s	49,7633864	53,8400154	55,33149561	55,4541898	61,2656449
Kt1	0,03358903	0,01579395	0,023010374	0,02394742	0,00961631
Kt2	0,0233556	0,01108017	0,016084671	0,01673184	0,00676715
Ut	0,01651716	0,0078351	0,011374316	0,01183202	0,00478515
SStot	3591199,01	3591199,01	3573130,456	3573130,46	3573130,46
R^2	0,91725121	0,90233111	0,898036929	0,89844487	0,87499364

Таблица 15

Наилучшие прогностические характеристики имеет модель ARIMA(4,4,1), но она имеет худшие информационные характеристики. Наилучшие информационные характеристики (наибольший R^2) имеет модель ARIMA(4,3,1), но эта модель имеет худшие прогностические характеристики.

Также можно оценить модели с помощью таких информационных критериев, как критерий Акаике (AIC), Шварца (SIC) и критерий окончательной ошибки (FPE).

критерий Акаике:

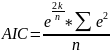
критерий Шварца:

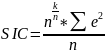
критерий окончательной ошибки:

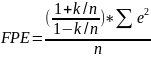
	ARIMA(4,3,1)	ARIMA(3,3,1)	ARIMA(3,4,2)	ARIMA(4,4,2)	ARIMA(4,4,1)
AIC	2575,34042	2991,44178	3184,885646	3223,72175	3904,65838
SIC	2884,73489	3274,81543	3568,471722	3695,07833	4374,93353
FPE	2575,45041	2991,50717	3185,024987	3223,96558	3904,82921

Таблица 16

Исходя из этого, лучшей из рассмотренных моделей является ARIMA(3,3,1), так как она имеет лучшие прогностические характеристики после модели ARIMA(4,4,1) и лучшие информационные характеристики после модели ARIMA(4,3,1).

Полученная модель имеет вид: 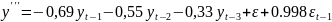, где

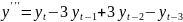
Если перестроить модель по всей выборке, то она имеет вид:

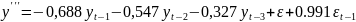
Точечный прогноз на 130 период = 1030,16, дисперсия остатков = 2625,29 с 122 степенями свободы.

Оценим доверительные интервалы для наилучшего варианта по формуле:

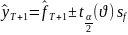, где

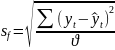
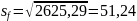
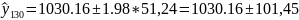
Значение индекса находится в интервале от 928,71 до 1131,61.

Этап 5. Спектральный анализ временного ряда. Оценка сезонных колебаний. Оценка точности прогнозирования уровня показателя.

На этапе 3 было определено, что во временном ряде существует тенденция и была выбрана лучшая из рассмотренных моделей для описания тренда – кривая Гомперца. За основу для спектрального анализа возьмем остатки этой модели.

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2025442.4 Кб0Логистика.docx
#
01.03.2025475.14 Кб0ЛР № 1 (обработка данных).doc
#
11.11.2019303.62 Кб3Лр №1 Знакомство с окном БД.doc
#
11.11.2019235.52 Кб13Лр №10 Защита базы данных.doc
#
11.11.2019113.66 Кб5Лр №9 Основы SQL.doc
#
18.07.20191.44 Mб4ЛР1 Журавлева М.docx
#
29.08.201976.14 Кб3ЛР1.docx
#
02.09.201972.19 Кб2ЛР2.doc
#
29.08.2019311.71 Кб3ЛР2.docx
#
29.08.201996.17 Кб3ЛР3.docx
#
29.08.201968.48 Кб4ЛР4.docx