Квадратичное экспоненциальное сглаживание

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет управления

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЛР1 Журавлева М.docx

Скачиваний:

Добавлен:

18.07.2019

Размер:

1.44 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Квадратичное экспоненциальное сглаживание

Общий вид модели квадратичного экспоненциального сглаживания Брауна имеет вид:

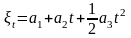
Начальные условия для сглаживающего полинома заданы следующим образом:

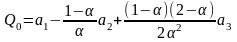
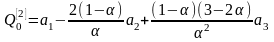
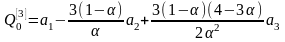
Экспоненциальные средние первого, второго и третьего порядков могут быть подсчитаны по следующим формулам:

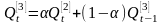
Оценки коэффициентов модели:

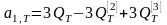
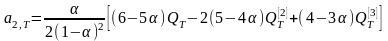
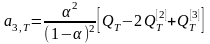
Окончательно точечный прогноз по модели экспоненциального среднего второго порядка на момент времени T:

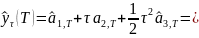
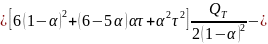
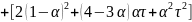
В приложении 6 построено несколько вариантов модели линейного экспоненциального сглаживания Брауна в зависимости от значения сглаживающего параметра Результаты сглаживания в сводной таблице 7:

период	значение показателя	экспоненциальная средняя
период	значение показателя	a=0,1	a=0,3	a=0,5	a=0,8	a=0,3531
1	813,17	861,146	814,74	783,895	732,226	803,298
2	877,02	845,326	794,965	785,901	813,206	787,931
3	844,36	851,921	848,244	896,26	977,135	857,167
4	856,69	847,596	844,507	857,72	801,865	849,218
5	924,97	847,978	854,57	865,241	864,672	859,314
6	953,18	868,932	920,602	965,321	1020,66	934,628
7	892,74	894,311	972,216	1004,46	988,606	985,721
8	874,46	896,488	934,291	894,653	792,59	929,615
9	771,4	892,581	895,981	846,36	838,254	883,625
10	785,72	858,365	784,49	694,82	634,264	757,283
11	829,36	835,151	752,224	727,374	817,869	736,271
12	865,08	829,769	784,874	826,886	914,135	787,745
13	892,15	836,427	837,415	900,716	922,48	851,965
14	947,28	850,144	887,073	939,316	922,79	904,471
15	948,6	877,869	956,984	1007,33	1012,53	976,906
16	992,79	900,555	983,447	991,242	937,649	993,908
17	1017,36	931,878	1027,25	1032,49	1038,9	1034,89
18	997,49	964,079	1059,7	1053,5	1042,36	1062,6
19	911,97	983,45	1046,07	1005,66	957,077	1037,82
20	837,21	972,67	954,352	861,218	782,652	928,054
21	857,42	940,898	843,423	745,955	735,421	809,134
22	798,01	920,933	817,003	799,108	906,309	798,912
23	859,33	886,769	759,62	747,226	738,163	745,944
24	849,27	877,62	799,269	858,468	954,708	807,128
25	838,65	867,307	815,916	865,842	846,499	828,638
26	824,31	855,958	819,029	847,347	818,558	830,251
27	820,56	842,73	811,429	821,561	802,7	818,941
28	821,28	831,244	808,19	815,023	817,437	814,089
29	812,44	822,573	810,593	819,213	826,261	816,155
30	786,55	813,347	806,271	809,017	802,651	809,84
31	804,84	798,604	783,249	771,449	751,581	782,198
32	834,95	792,741	792,346	801,22	833,533	795,135
33	863,61	797,606	825,915	854,137	882,55	834,341
34	816,88	810,63	866,882	897,733	901,928	877,875
35	862,39	807,505	840,563	818,929	743,505	839,098
36	839,67	819,02	867,871	873,124	918,755	870,44
37	812,22	821,781	857,178	841,604	811,117	854,188
38	822,04	816,022	825,51	793,592	768,937	816,553
39	823,26	814,594	820,002	808,602	838,033	814,122
40	843,39	814,076	819,357	818,902	831,107	816,396
41	865,42	819,954	837,941	853,136	872,863	840,03
42	825,66	831,506	865,855	887,457	895,408	871,491
43	850,26	829,008	840,67	822,958	764,967	837,622
44	828,34	834,488	850,569	850,384	879,734	850,282
45	783,02	832,404	834,466	821,167	801,53	830,756
46	807,71	817,205	786,369	751,574	718,556	775,974
47	791,73	812,525	789,594	792,352	847,108	786,829
48	829,32	804,154	779,612	782,883	779,153	778,335
49	863,65	808,923	811,912	843,341	883,021	819,095
50	878,19	823,269	858,409	899,162	912,806	870,933
51	894,68	839,294	890,405	913,825	890,984	900,991
52	873,43	857,14	915,474	923,57	906,903	922,416
53	841,42	865,008	902,232	877,913	835,244	899,62
54	923,94	861,545	863,084	818,177	790,898	851,808
55	919,01	883,331	918,22	941,244	1042,17	921,198
56	919,19	899,11	935,288	943,864	916,444	937,19
57	881,18	911,479	938,573	931,596	906,988	937,138
58	911,06	909,572	901,571	864,877	821,78	891,572
59	921,6	916,547	910,056	904,828	952,143	905,631
60	1016,39	924,861	922,193	928,581	942,046	921,423
61	1055,37	959,496	1011,33	1070,52	1146,44	1025,9
62	1103,51	998,412	1080,57	1125,03	1102,35	1096,25
63	1112,47	1043,29	1145,06	1170,75	1148,59	1158,01
64	1119,03	1080,97	1169,31	1155,42	1104,79	1171,77
65	1113,04	1111,91	1173	1136,76	1110,3	1166,4
66	1028,2	1133,51	1157,68	1110,07	1094,86	1144,17
67	1038,78	1123,84	1065,53	974,074	904,718	1036,86
68	1086,43	1117,72	1031,18	989,284	1056,32	1009,91
69	1105,96	1125,7	1060,21	1084,19	1169,71	1056,45
70	1125,8	1136,65	1091,7	1129,49	1138,16	1096,84
71	1124,88	1150,09	1122,63	1155,67	1145,47	1131,18
72	1162,68	1159,29	1132,92	1143,89	1114,58	1138,38
73	1204,92	1176,69	1168,31	1188,39	1207,97	1176,3
74	1232,24	1201,99	1217,69	1244,74	1259,37	1228,26
75	1138,69	1229,11	1257,7	1273,45	1260,16	1266,28
76	1230,79	1221,32	1183,02	1114,96	993,924	1169,12
77	1271,72	1241,2	1228,29	1235,29	1352,06	1227,61
78	1307,78	1268,01	1281,32	1310,55	1339,08	1287,83
79	1328,18	1298,84	1330,86	1355,97	1346,21	1338,94
80	1310,47	1328,11	1362,54	1367,98	1340,63	1366,91
81	1326,15	1344,56	1350,99	1320,41	1270,83	1345,27
82	1344,56	1360,69	1351,76	1326,96	1338,55	1344,38
83	1348,83	1377,37	1362,16	1350,79	1368,98	1356,63
84	1324,74	1390,24	1364,9	1354,38	1351,33	1359,5
85	1347,72	1391,55	1339,49	1313,08	1285,78	1329,9
86	1213,49	1397,76	1346,03	1343,83	1377,57	1341,67
87	1145,62	1360,8	1226,25	1147,24	1028,15	1202,58
88	1180,98	1309,29	1115,78	1044,46	1053,44	1088,91
89	1181,07	1277,44	1109,59	1129,86	1258,46	1104,08
90	1145,27	1251,18	1119,28	1171,67	1206,69	1127,49
91	995,52	1218,87	1101,71	1134,53	1100,12	1110,8
92	957,73	1147,78	968,505	914,125	787,831	957,022
93	1030,47	1079,5	889,518	865,539	917,9	880,989
94	987,7	1047,11	938,323	1016,42	1167,42	955,737
95	874,21	1009,24	936,623	990,751	949,403	954,863
96	749,78	945,949	845,306	822,654	712,648	846,184
97	815,25	859,262	706,331	639,905	584,546	691,594
98	788,89	811,195	722,874	767,515	937,255	731,444
99	688,15	766,982	724,943	779,255	787,106	740,556
100	689,85	703,76	649,98	643,801	552,754	653,379
101	758,83	656,245	633,533	653,916	701,045	641,866
102	813,63	641,779	703,196	783,644	877,662	728,073
103	820,49	649,673	792,849	882,2	898,507	825,177
104	906,61	661,018	840,726	881,35	818,074	864,254
105	902,04	698,698	936,386	984,07	1010,02	960,744
106	941,57	730,019	966,276	956,483	882,816	975,15
107	988,37	769,097	1004	982,89	976,282	1005,2
108	1024,29	816,235	1050,72	1033,29	1043,1	1048,84
109	1117,68	866,195	1090,33	1068,8	1061,6	1084,94
110	1125,11	935,253	1177,62	1187,79	1232,54	1178,73
111	1142,6	993,404	1206,12	1178,38	1117,92	1198,39
112	1196,45	1045,34	1216,96	1170,7	1142	1202,25
113	1193,84	1102,8	1254,38	1229,04	1257,81	1242,38
114	1163,26	1147,41	1253,54	1211,35	1179,49	1236,8
115	1141,02	1172,96	1212,34	1147,23	1106,34	1188,06
116	1170,72	1185,52	1164,94	1104,77	1104,87	1139,22
117	1132,32	1203,15	1166,35	1154,78	1217,14	1152,09
118	1143,91	1204,38	1130,24	1109,76	1084,34	1116,46
119	1120,08	1207,43	1124,78	1129,17	1159,04	1118,87
120	1128,26	1201,37	1102,47	1102,88	1092,03	1098,3
121	1207,35	1197,67	1102,69	1119,3	1141,56	1104,39
122	1148,54	1217,23	1177,08	1245,45	1322,54	1194,83
123	1163,89	1214,12	1156,78	1160,05	1063,83	1162,81
124	1166,96	1215,04	1160,61	1163,96	1171,96	1165,31
125	1156,66	1215,58	1164,66	1168,24	1174,15	1168,44
126	1155,66	1211,87	1156,68	1152,13	1142,08	1157,63
127	1134,28	1207,59	1152,17	1149,61	1153,76	1152,55
128	1104,87	1196,83	1131,33	1119,6	1105,97	1128,69
129	1055,55	1178,54	1097,05	1077,59	1065,65	1091,26
130		1185,29	1078,06	1043,32	1016,63	1068,48

Таблица 7

Посчитаем информационные и прогностические характеристики.

Где m=3

Результаты расчетов в сводной таблице 8.

модель	a	Характеристики модели
модель	a	R^2	s^2	Kt1	Kt2	Ut
квадратичной экспоненциальной средней	a=0,1	0,720802727	8164,649081	0,11652	0,077739	0,055053
	a=0,3	0,89422666	3093,161304	0,039315	0,027259	0,019279
	a=0,5	0,882301543	3441,89106	0,020884	0,014614	0,010334
	a=0,8	0,785752594	6265,300757	0,009566	0,006732	0,00476
	a=0,3463	0,895623322	3052,318306	0,033826	0,023518	0,016632

Таблица 8

Лучшие прогностические характеристики из моделей квадратичного экспоненциального сглаживания имеет модель со значением а=0,8. По информационным характеристикам (R^2 89) можно выделить 3 модели: а=0,3, а=0,5 и а=0,3463. Из этих моделей лучшими прогностическими характеристиками обладает модель с параметром а=0,5.

Составим таблицу для лучших из рассмотренных тремя методами моделей:

модель	a	Характеристики модели
модель	a	R^2	s^2	Kt1	Kt2	Ut
экспоненциальной средней	a=0,95	0,921530921	20,35529531	0,048168	0,03325	0,023518
линейной экспоненциальной средней	a=0,6	0,909006918	2639,819257	0,033543	0,023324	0,016495
квадратичной экспоненциальной средней	a=0,5	0,882301543	3441,89106	0,020884	0,014614	0,010334

Таблица 9

Лучшей по информационным характеристикам является модель простого экспоненциального сглаживания. По прогностическим характеристикам – квадратичного экспоненциального сглаживания.

Models

(A) Simple exponential smoothing with alpha = 0,95

(B) Brown's linear exp. smoothing with alpha = 0,6

Model	RMSE	RUNS	RUNM	AUTO	MEAN	VAR
(A)	47,3383	OK	OK	OK	OK	*
(B)	50,9762	OK	OK	*	OK	*
(C)	57,976	OK	OK	**	OK	*

Из таблицы видно, что в остатках моделей линейного и квадратичного экспоненциального сглаживания присутствует автокорреляция. Поэтому целесообразно выбрать модель простого экспоненциального сглаживания, хотя ни одна из моделей не проходит тест на равенство дисперсий.

Построим интервальные прогнозы для простого экспоненциального сглаживания по формуле:

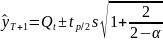
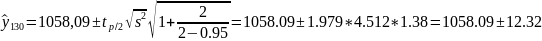
Значение индекса в периоде 130 находится в интервале между 1045,77 и 1070,41.

Этап 3. Сглаживание временного ряда с использованием модели тренда. Оценка точности прогнозирования уровня показателя.

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2025442.4 Кб0Логистика.docx
#
01.03.2025475.14 Кб0ЛР № 1 (обработка данных).doc
#
11.11.2019303.62 Кб3Лр №1 Знакомство с окном БД.doc
#
11.11.2019235.52 Кб13Лр №10 Защита базы данных.doc
#
11.11.2019113.66 Кб5Лр №9 Основы SQL.doc
#
18.07.20191.44 Mб4ЛР1 Журавлева М.docx
#
29.08.201976.14 Кб3ЛР1.docx
#
02.09.201972.19 Кб1ЛР2.doc
#
29.08.2019311.71 Кб3ЛР2.docx
#
29.08.201996.17 Кб3ЛР3.docx
#
29.08.201968.48 Кб4ЛР4.docx