
- •Материалы к самостоятельному изучению темы «Применение производной» і. Исследование функций и построение графиков.
- •Найти область определения функции: д(у).
- •Исследовать функцию на четность, нечетность, периодичность.
- •Найти точки пересечения с осями координат (если это возможно элементарным путем):
- •5. Найти все асимптоты графика функции.
- •Іі. Наибольшее и наименьшее значение функции на отрезке.
- •Ііі. Примеры.
Материалы к самостоятельному изучению темы «Применение производной» і. Исследование функций и построение графиков.
Схема исследования:
Найти область определения функции: д(у).
Определение: Д(у) – это область допустимых значений переменной Х, при которых функция имеет смысл.
Найти точки разрыва функции и ее односторонние пределы:
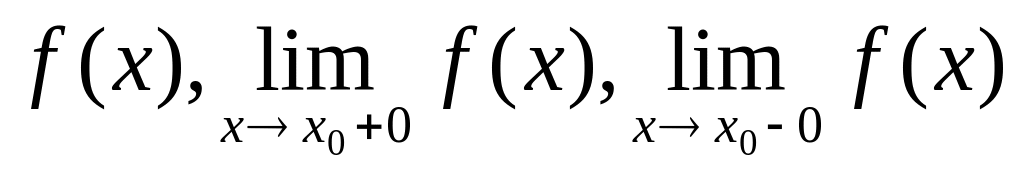 .
.
Исследовать функцию на четность, нечетность, периодичность.
Определение: Функция у = f (x) называется четной, если для любых значений х из Д(у) выполняется условие f (-x)= f (x).
Определение: Функция у = f (x) называется нечетной, если для любых значений х из Д(у) выполняется условие f (-x)= -f (x).
Определение: Функция у = f (x) называется общего вида (ни четной, ни нечетной), если для любых значений х из Д(у) f (-x)≠ -f (x) и f (-x)≠ f (x).
При построении графиков учесть, что график четной функции симметричен относительно оси ОУ, а нечетной – относительно начала координат.
Определение: Функция у = f (x) называется периодичной с периодом Т≠0 , если для любых значений х из Д(у) выполняется условие f (x+Т)= f (x).
Найти точки пересечения с осями координат (если это возможно элементарным путем):
а) с осью ОХ: у=0, вычисляем х
б)с осью ОУ: х=0, вычисляем у.
5. Найти все асимптоты графика функции.
Определение: Асимптотой графика функции у = f (x) называется прямая, к которой неограниченно приближается точка кривой при неограниченном удалении её от начала координат.
Виды асимптот:
горизонтальная асимптота
Пример:
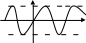

Определение: Кривая у = f (x) имеет
горизонтальную асимптоту у = b только в
том случае, когда существует конечный
предел функции
![]()
![]() .
.
Замечание: Если конечен
только один из пределов
![]() или
или
![]() ,
то функция имеет лишь левостороннюю
,
то функция имеет лишь левостороннюю
![]() или правостороннюю
или правостороннюю
![]() горизонтальную
асимптоту.
горизонтальную
асимптоту.
вертикальная асимптота
Пример:
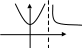
Определение: Кривая у = f (x) имеет
вертикальную асимптоту
![]() ,
если хотя бы один из пределов
,
если хотя бы один из пределов
![]() или
или
![]() равен бесконечности.
равен бесконечности.
Замечание: 1. Вертикальные асимптоты следует искать в точках разрыва функции у = f (x) или на концах ее области определения.
2. Если функция непрерывна
в точке![]() ,
то в точке
вертикальных асимптот быть не может.
,
то в точке
вертикальных асимптот быть не может.
3) наклонные асимптоты:
Определение: Кривая у = f (x) имеет
наклонную асимптоту
![]() ,
если существуют конечные пределы:
,
если существуют конечные пределы:
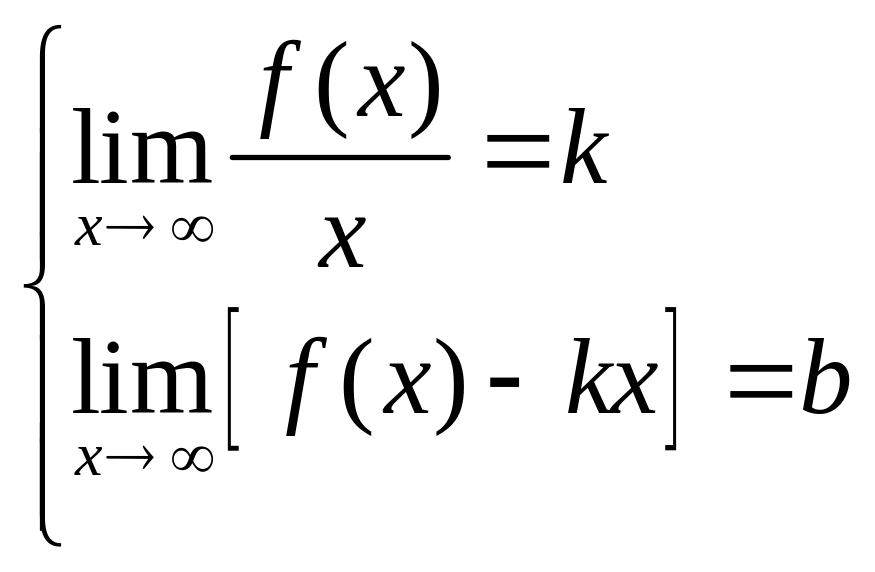
Замечание: 1.Если при вычислении k=0, то у = b – горизонтальная асимптота.
2.Следует отдельно
рассматривать случаи
![]() .
.
Найти точки экстремума и интервалы возрастания и убывания функции.
Определение: Функция у = f (x)
называется возрастающей на
промежутке
![]() ,
если для любых значений
,
если для любых значений
![]() и
и
![]() из
этого промежутка из неравенства
из
этого промежутка из неравенства
![]() вытекает неравенство
вытекает неравенство
![]() (т.е.
большему значению аргумента соответствует
большее значение функции).
(т.е.
большему значению аргумента соответствует
большее значение функции).
Определение: Функция у = f (x)
называется убывающей на промежутке
,
если для любых значений
и
из
этого промежутка из неравенства
вытекает неравенство
![]() (т.е.
большему значению аргумента соответствует
меньшее значение функции).
(т.е.
большему значению аргумента соответствует
меньшее значение функции).
Возрастающая и убывающая – это строго монотонные функции.
Определение: Функция у = f (x)
называется неубывающей на
промежутке
,
если для любых значений
и
из
этого промежутка из неравенства
вытекает неравенство
![]() .
.
Определение: Функция у = f (x)
называется невозростающей на
промежутке
,
если для любых значений
и
из
этого промежутка из неравенства
вытекает неравенство
![]() .
.
Невозрастающая и неубывающая - это монотонные функции.
Теорема (достаточное условие возрастания функции)
Если производная функции у = f (x) положительная внутри некоторого промежутка, то в этом промежутке функция возрастает.
Теорема (достаточное условие убывания функции)
Если
![]() внутри некоторого промежутка, то она
убывает на этом промежутке.
внутри некоторого промежутка, то она
убывает на этом промежутке.
Интервалы возрастания и убывания функции – это интервалы монотонности.
Экстремумы функции – это значение функции в точках экстремума.
Точки экстремума – это точки максимума и минимума.
Определение: Точка
называется точкой максимума функции у
= f (x), если в некоторой открытости
точки
выполняется неравенство
![]() .
.
Определение: Точка
- называется точкой минимума функции
у = f (x), если в некоторой окрестности
точки
выполняется неравенство:![]() .
.
Теорема 1(необходимое и достаточное условие экстремума)
Для того чтобы точка являлась точкой максимума необходимым и достаточным является выполнение двух условий:
- должна являться критической точкой (критические точки – это точки, в которых производная равна нулю или совсем не существует);
при переходе через точку производная меняет свой знак с «+» на «–».
Теорема 2(необходимое и достаточное условие экстремума)
Для того чтобы точка являлась точкой минимума необходимым и достаточным является выполнение двух условий:
1. - должна являться критической точкой (критические точки – это точки, в которых производная равна нулю или совсем не существует);
2. при переходе через точку производная меняет свой знак с «–» на «+».
Схема нахождения интервалов возрастания, убывания и экстремумов функции.
Найти
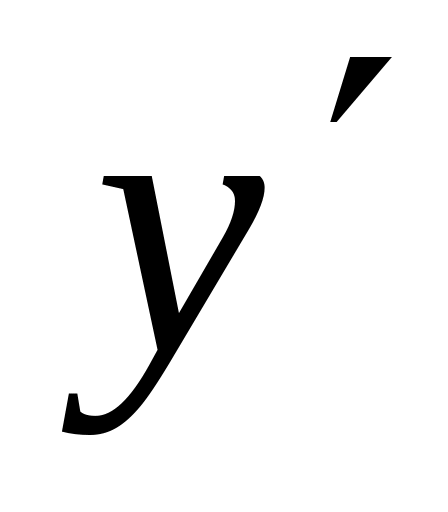 (х).
(х).Найти критические точки.
Исследовать знак производной слева и справа от каждой критической точки.
Сделать вывод об интервалах возрастания и убывания функции, о наличии точек экстремума и найти экстремумы функции.
Примечание: Данное задание удобно выполнять с помощью таблицы:
Пусть
![]() - критические точки, причем
- критические точки, причем
![]()
|
|
|
|
|
|
|
|
|
+ |
0 |
+ |
0 |
– |
0 |
+ |
|
|
- |
|
|
|
|
|
нет экстремума |
max |
min |
Найти точки перегиба графика функции и интервалы его выпуклости вверх и вниз.
Определение: В некотором интервале кривая у = f (x) называется выпуклой вверх(выпуклой), если она лежит выше касательной проведенной в любой ее точке.
Определение: В некотором интервале кривая у = f (x) называется выпуклой вниз (вогнутой), если она лежит ниже касательной проведенной в любой ее точке.
Определение: Точка перегиба - это точка на кривой, в которой меняется направление её выпуклости.
Теорема (условия перегиба)
Точка - будет являться точкой перегиба, если выполняются следующие условия:
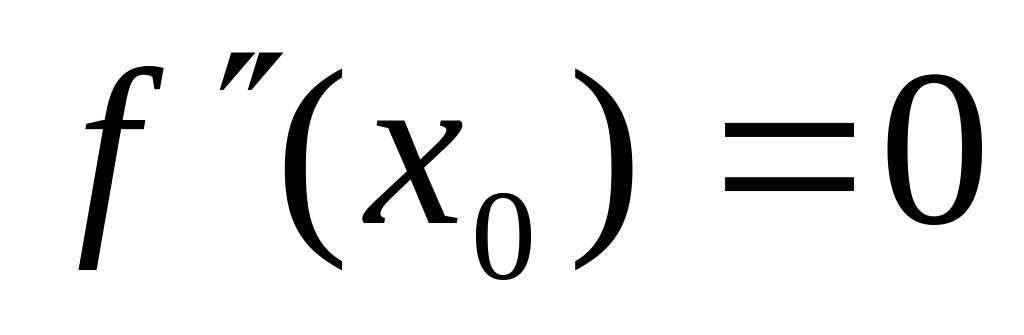 .
.При переходе через точку
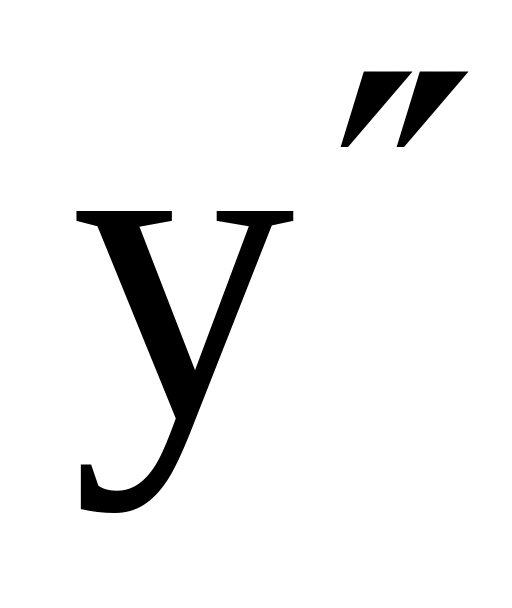 меняет свой знак. Причем, если:
меняет свой знак. Причем, если:
– в некотором интервале
![]() ,
то кривая вогнута
,
то кривая вогнута
![]() ,
,
– в некотором интервале
![]() ,
то кривая выпукла
,
то кривая выпукла
![]() .
.
Схема нахождения интервалов выпуклости и вогнутости:
Найти
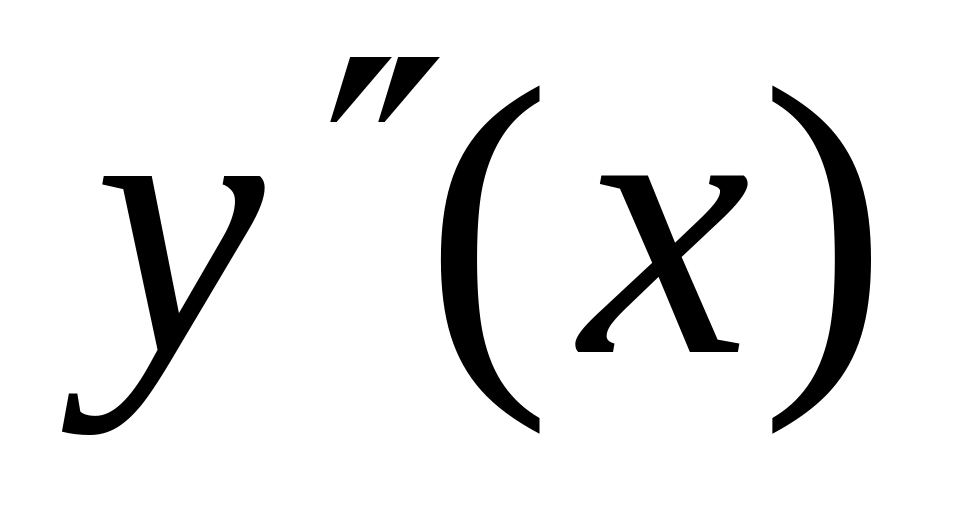 .
.Найти точки, в которых
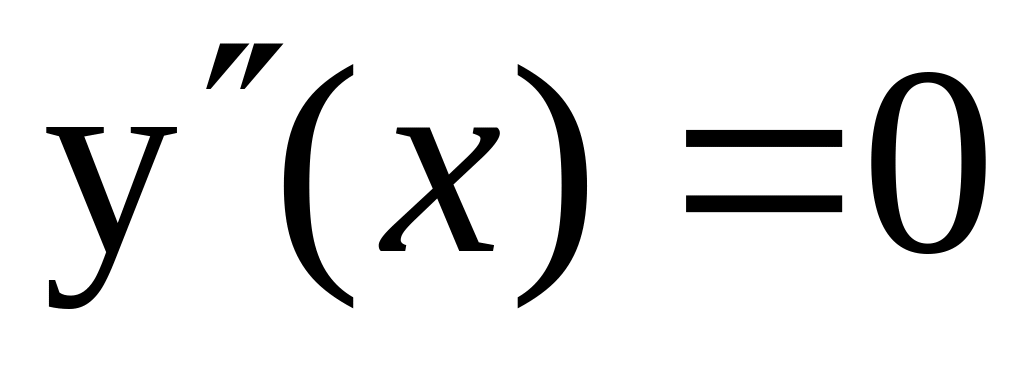 или не существует.
или не существует.Исследовать знак второй производной слева и справа от найденных точек. Сделать вывод.
Найти значение функции в точках перегиба.
Таблица для выполнения 7 задания:
-

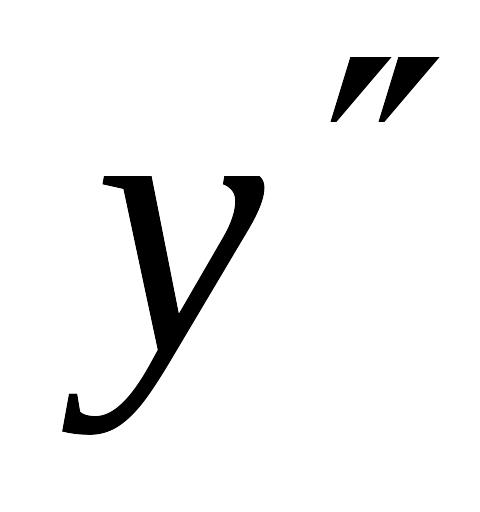
–
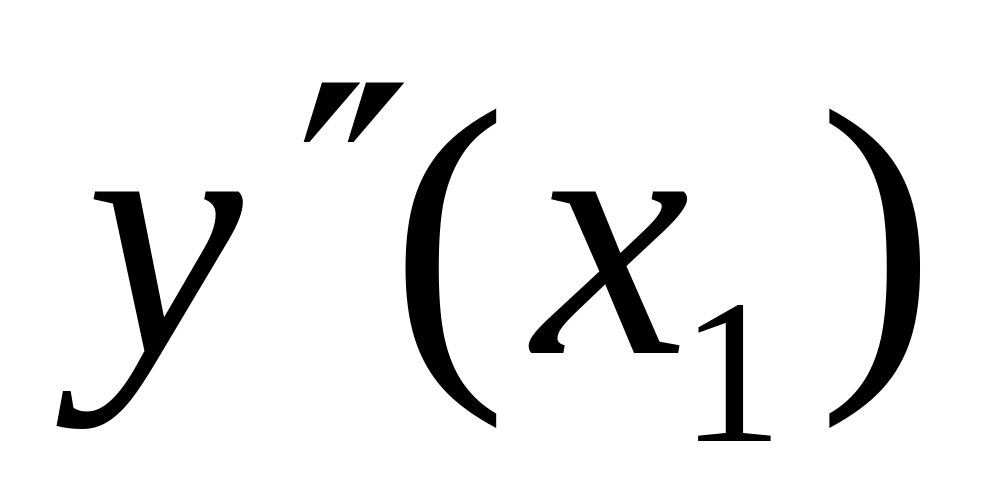 =0
=0+
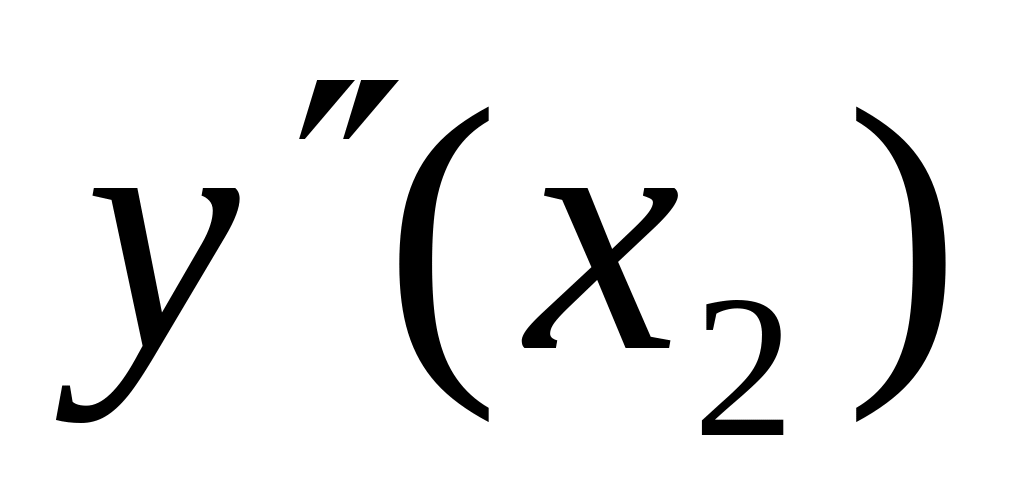 =0
=0+
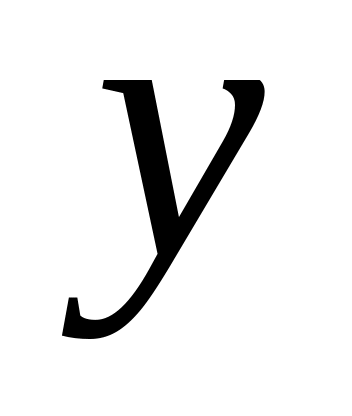
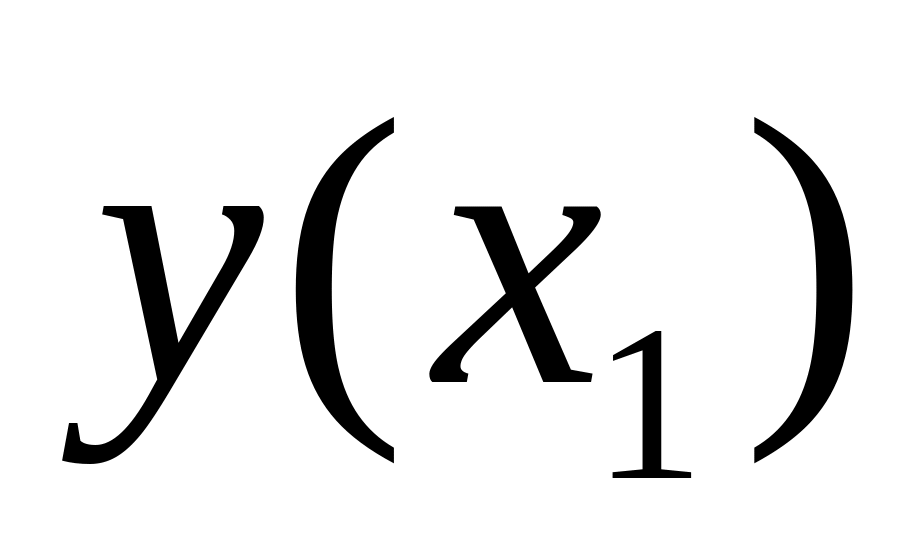

Построить график функции, используя все полученные результаты исследования. При необходимости следует найти дополнительно несколько точек графика функции.



