6 Построение областей устойчивости
Для выделения областей устойчивости в пространстве параметров системы, описываемой уравнением любого порядка, в соответствии с условием устойчивости по Ляпунову, необходимо и достаточно, чтобы корни характеристического уравнения системы имели отрицательные вещественные части. Область устойчивости находится в левой полуплоскости относительно мнимой оси.
Для построения областей устойчивости методом Д-разбиения по коэффициенту усиления системы K запишем характеристическое уравнение замкнутой системы, выделив коэффициент K:
где
- коэффициент усиления замкнутой системы.
Произведем замену: S j, тогда характеристическое уравнение будет выглядеть следующим образом:
Координаты характерных точек приведены в таблице 4.
Таблица 4 – Данные для построения границы Д-разбиения
-
0
-1,205
3,172
10,866
R()
-1
-2,1
1,524
7,062
I()
0
-1,566
0
188,952
График области устойчивости представлен на рисунке 4.
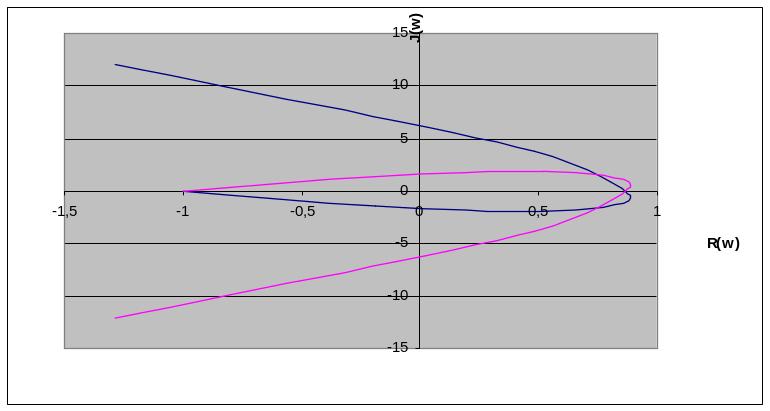
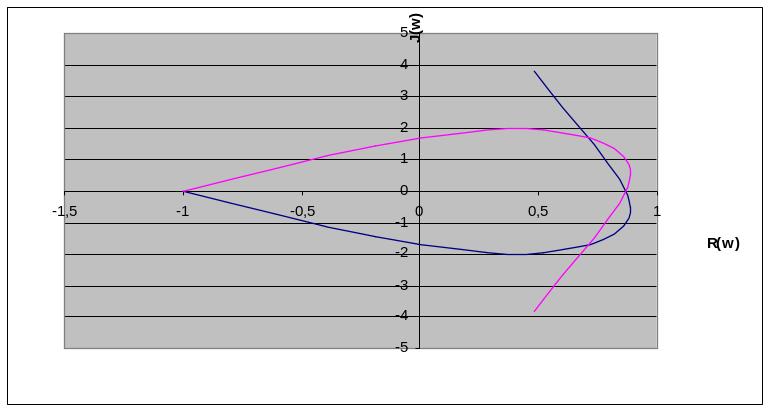
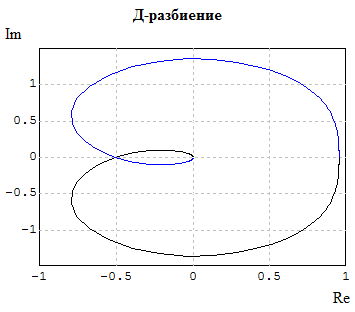
Рисунок 4 – графики Д-разбиения.
На основании полученной кривой Д-разбиения устанавливаем, что данная система будет устойчива при любом значении коэффициента усиления K в пределах от до 0,78. Значение K=0,78 называется критическим коэффициентом усиления.
7 Моделирование в системе мвту
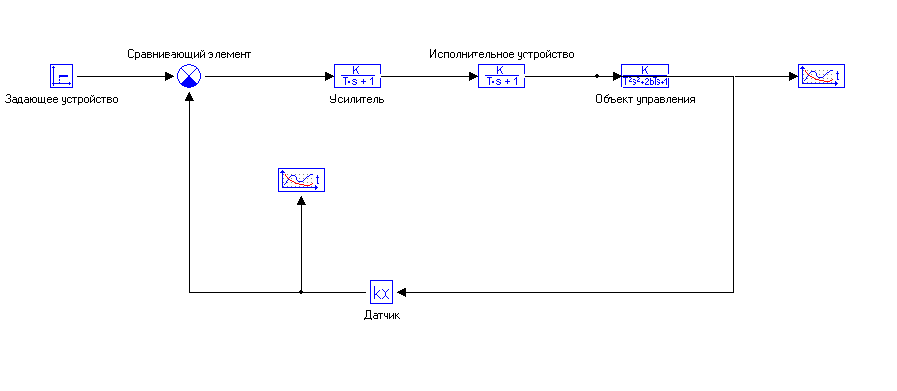
Рисунок 5 – принципиальная схема системы управления.
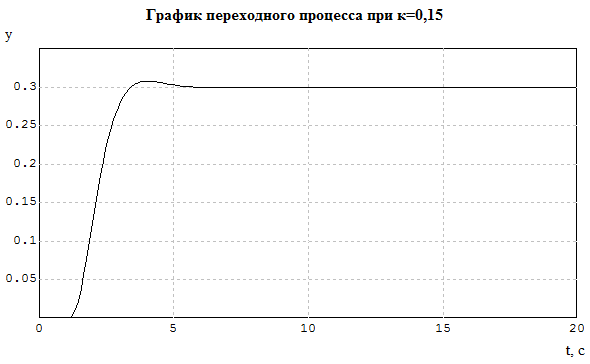
8 Показатели качества работы в установившемся и переходном режимах
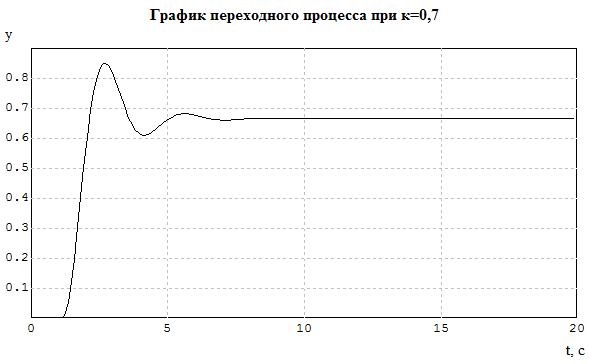
0,851
2,705
0,683
5,611
6,979
0,666
δ
27,78%
2,906
Используя
по
критерию Гурвица для устойчивости
необходимо и достаточно а3<а2*а1 , если
левая часть неравенства будет в несколько
раз меньшей чем правая , то НЧ будет
иметь хороший запас устойчивости.
0,161 <
0,818*1,62=1,33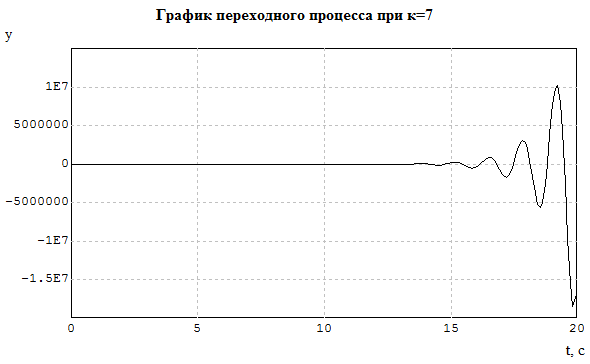
9 Определение запасов устойчивости по амплитуде и фазе, построение графика логарифмической амплитудной характеристики и фазовой частотной характеристики
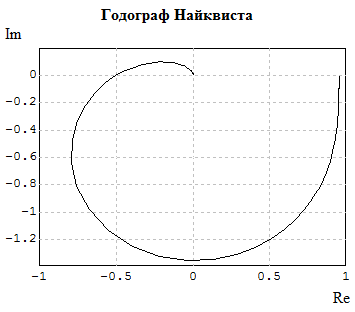
Устойчивость разомкнутого контура является условием практического применения критерия Найквиста => можно построить АЧХ и ФЧХ, т.е. оценить устойчивость замкнутой системы с помощью критерия Найквиста
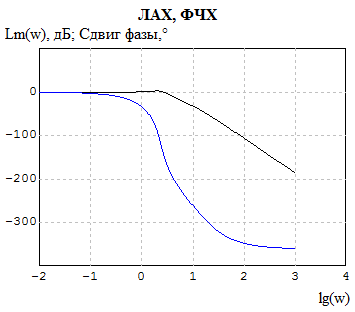
Рисунок 6 – Логарифмическая амплитудная характеристика и фазовая частотная характеристики
Так как ФЧХ
пересекает линию -180° раньше чем
-
0 ДБ =>
система устойчива
10 Список литературы
Анхимюк, В. Л. Теория автоматического регулирования [Текст] / В. Л. Анхимюк. – М. : ООО «Издательство АСТ», 2000. – 504 с.
Афанасьев, В. Н. Математическая теория конструирования систем управления [Текст] : учеб. для вузов / В. Н. Афанасьев, В. Б. Колмановский, В. Р. Носов. – М. : Высшая школа, 1998. – 574 с.
Евсюков, В. Н. Анализ автоматических систем [Текст]: учебно-методическое пособие для выполнения практических заданий / В. Н. Евсюков, А. М. Черноусова. – 2-е изд., исп. – Оренбург: ИПК ГОУ ОГУ, 2007. - 179 с.
Ерофеев, А. А. Теория автоматического управления [Текст] / А. А. Ерофеев. – СПб. : Политика, 1998. – 295 с.
Зарубин, В. С. Математическое моделирование в технике [Текст]: учеб. для вузов / Под ред. В. С.Зарубина, А. П. Крищенко. - М.: Изд-во МГТУ им.Н.Э.Баумана, 2001. – 496 с.
Первозванский, А. А. Курс теории автоматического регулирования [Текст] / А. А. Первозванский. – М. : Наука, 1992. – 522 с.