Московский Авиационный Институт (Государственный Технический Университет)
Лабораторная работа №3.
Экспериментальное определение закона распределения случайной величины.
Вариант №12.
Выполнил: студент гр. 04-212
Кувакин Дмитрий
Проверил: Рудненко Александр Васильевич
Москва 2011
Содержание
Теоретическая справка……………………………………………..……………3
Расчетная часть при выборке состоящей из n=30 элементов…..………….…5
Расчетная часть при выборке состоящей из n=100 элементов.. .………….…8
Расчетная часть при выборке состоящей из n=200 элементов….…………..11
Таблица распределения хи-квадрат Пирсона………………….…..…….…..16
Цель работы: Ознакомить студентов с методами оценивания параметров закона распределения случайной величины по результатам эксперимента и способом проверки гипотез о законе распределения с помощью критерия согласия хи-квадрат Пирсона.
Теоретическая справка. Математическое ожидание
Рассмотрим случайную величину с числовыми значениями. Часто оказывается полезным связать с этой функцией число — её «среднее значение» или, как говорят, «среднюю величину», «показатель центральной тенденции». По ряду причин, некоторые из которых будут ясны из дальнейшего, в качестве «среднего значения» обычно используют математическое ожидание.
Математическим ожиданием случайной величины X называется число
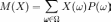 ,
,
то есть математическое ожидание случайной
величины — это взвешенная сумма значений
случайной величины с весами, равными
вероятностям соответствующих элементарных
событий. Если случайная величина X
принимает значения
 .
Тогда справедливо равенство
.
Тогда справедливо равенство
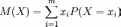 ,
,
Пусть X — случайная величина, M(X) — её математическое ожидание, a — некоторое число. Тогда
M(a) = a;
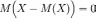 ;
;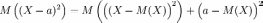 .
.
Дисперсия случайной величины
Математическое ожидание показывает,
вокруг какой точки группируются значения
случайной величины. Необходимо также
уметь измерить изменчивость случайной
величины относительно математического
ожидания. Выше показано, что
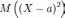 достигает
минимума по a при a = M(X).
Поэтому за показатель изменчивости
случайной величины естественно взять
именно
достигает
минимума по a при a = M(X).
Поэтому за показатель изменчивости
случайной величины естественно взять
именно
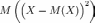 .
.
Дисперсией случайной величины X называется число
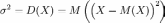 .
.
Установим ряд свойств дисперсии случайной величины, постоянно используемых в вероятностно-статистических методах принятия решений.
Пусть X — случайная величина, a и b — некоторые числа, Y = aX + b. Тогда
D(Y) = a2D(X).
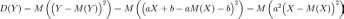 .
.
Пусть
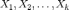 —
попарно независимые случайные величины
(то есть Xi и Xj
независимы, если
—
попарно независимые случайные величины
(то есть Xi и Xj
независимы, если
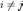 ).
Пусть Yk — их сумма,
).
Пусть Yk — их сумма,
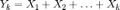 ,
тогда дисперсия суммы равна сумме
дисперсий слагаемых,
,
тогда дисперсия суммы равна сумме
дисперсий слагаемых,
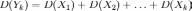 .
.
Для любых случайкых величин математическое ожидание суммы равно сумме математических ожиданий слагаемых,
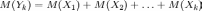 .
.
Хи-квадрат Пирсона.
С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. В дальнейших разделах книги много раз встречаются эти распределения.
Распределение Пирсона χ2 (хи-квадрат) — распределение случайной величины
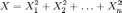 ,
,
где случайные величины
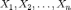 независимы
и имеют одно и тоже распределение N(0,1).
При этом число слагаемых, то есть n,
называется «числом степеней свободы»
распределения хи-квадрат.
независимы
и имеют одно и тоже распределение N(0,1).
При этом число слагаемых, то есть n,
называется «числом степеней свободы»
распределения хи-квадрат.
Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категорированных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных.
n=30 Смоделирована
выборка, состоящая из элементов: