
11.3. Поверхности второго порядка
11.3.1. Классификация поверхностей второго порядка
Алгебраической поверхностью
второго порядка называется
геометрическое место точек пространства,
которое в какой-либо аффинной системе
координат
![]() может быть задано уравнением вида
может быть задано уравнением вида
![]()
![]() ,
,
где старшие коэффициенты
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() не равны нулю одновременно. Без ограничения
общности можно считать, что система
координат, в которой задано уравнение
поверхности второго порядка, прямоугольная.
Для каждой поверхности второго порядка
существует прямоугольная система
координат
,
в которой уравнение принимает наиболее
простой (канонический) вид. Она
называется канонической, а
уравнение – каноническим.
не равны нулю одновременно. Без ограничения
общности можно считать, что система
координат, в которой задано уравнение
поверхности второго порядка, прямоугольная.
Для каждой поверхности второго порядка
существует прямоугольная система
координат
,
в которой уравнение принимает наиболее
простой (канонический) вид. Она
называется канонической, а
уравнение – каноническим.
Канонические уравнения поверхностей второго порядка

1.
![]() – уравнение эллипсоида;
– уравнение эллипсоида;
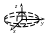
2.
![]() –
уравнение мнимого эллипсоида;
–
уравнение мнимого эллипсоида;
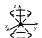
3.
![]() –
уравнение мнимого конуса;
–
уравнение мнимого конуса;

4.
![]() –
уравнение однополостного
–
уравнение однополостного
гиперболоида;
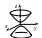
5.
![]() –
уравнение двуполостного
–
уравнение двуполостного
гиперболоида;

6.
![]() –
уравнение конуса;
–
уравнение конуса;

7.
![]() –
уравнение эллиптического
–
уравнение эллиптического
параболоида;

8.
![]() –
уравнение гиперболического
–
уравнение гиперболического
 параболоида;
параболоида;
9.
![]() –
уравнение эллиптического
–
уравнение эллиптического
цилиндра;
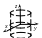
10.
![]() –
уравнение мнимого
–
уравнение мнимого
эллиптического цилиндра;
11.
![]() – уравнение пары мнимых
– уравнение пары мнимых
пересекающихся плоскостей;
1 2.
2.
![]() – уравнение гиперболического
– уравнение гиперболического
 цилиндра;
цилиндра;
13.
![]() – уравнение пары пересекающихся
– уравнение пары пересекающихся
 плоскостей;
плоскостей;
14.
![]() – уравнение параболического
– уравнение параболического
цилиндра;

15.
![]() – уравнение пары параллельных
– уравнение пары параллельных
плоскостей;
16.
![]() – уравнение пары мнимых
– уравнение пары мнимых
параллельных плоскостей;

17.
![]() – уравнение пары совпадающих
– уравнение пары совпадающих
плоскостей.
В этих уравнениях
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
причем
,
причем
![]() в уравнениях п.1–3;
в уравнениях п.1–3;
![]() в уравнениях п.4–7,9–11.
в уравнениях п.4–7,9–11.
Поверхности (1),(4)–(9), (12)–(15),(17) называются вещественными (действительными), а поверхности (2),(3),(10),(11),(16) – мнимыми. Вещественные поверхности изображены в канонических системах координат. Изображения мнимых поверхностей даются штриховыми линиями только для иллюстрации.
Поверхность второго порядка называется центральной, если она имеет единственный центр (симметрии). В противном случае, если центр отсутствует или не является единственным, поверхность называется нецентральной. К центральным поверхностям относятся эллипсоиды (вещественный и мнимый), гиперболоиды (однополостный и двуполостный), конусы (вещественный и мнимый). Остальные поверхности – нецентральные.
Алгоритм составления канонического уравнения поверхности второго порядка
Пусть в прямоугольной системе координат поверхность второго порядка описывается уравнением
.
Требуется определить ее название и составить каноническое уравнение. Для этого нужно выполнить следующие действия:
1. Вычислить ортогональные инварианты
![]() ,
,
![]() ,
,
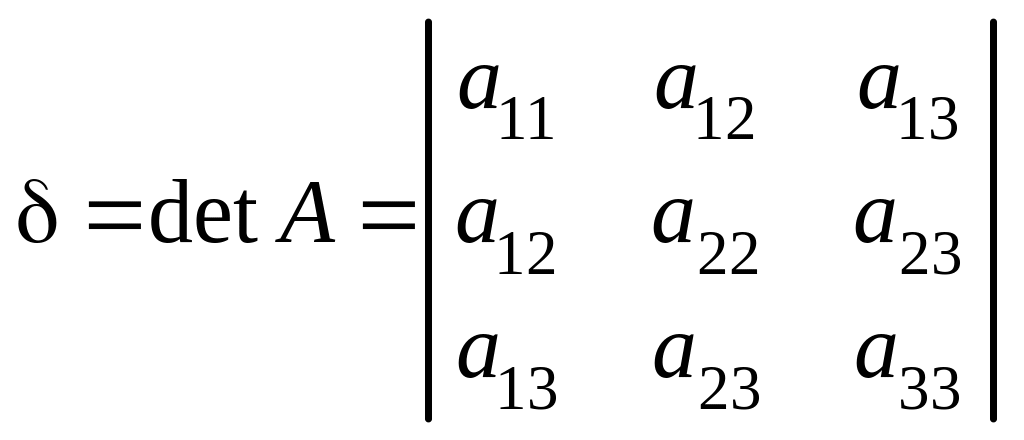 ,
,
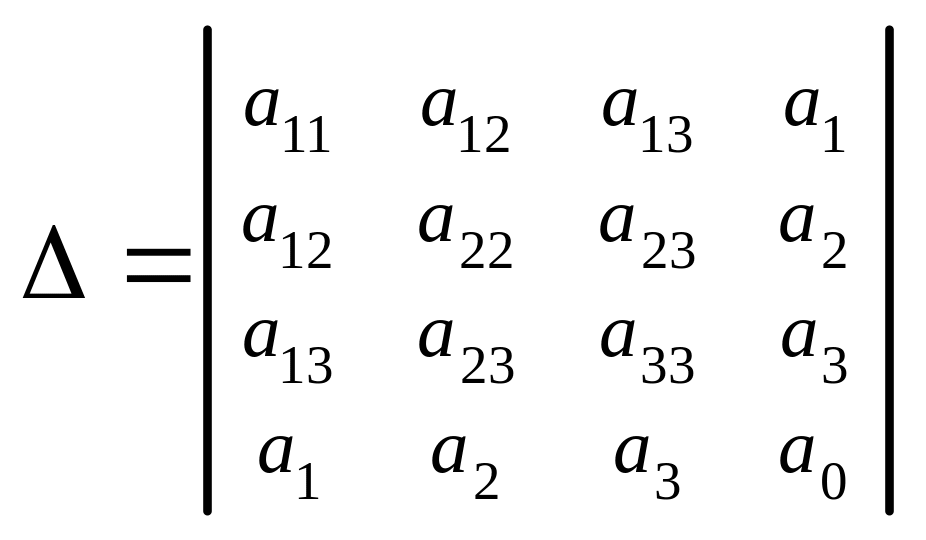 .
.
Если
![]() ,
то вычислить семиинвариант
,
то вычислить семиинвариант
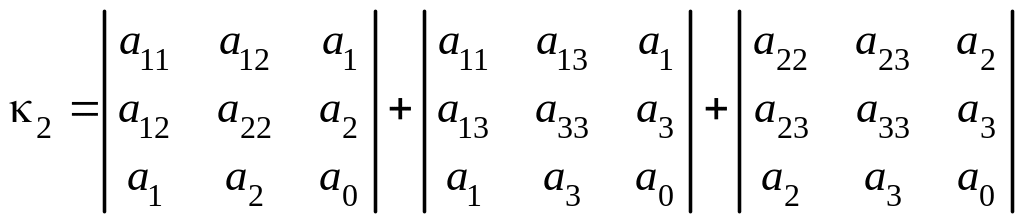 .
.
Если
и
![]() ,
то вычислить семиинвариант
,
то вычислить семиинвариант
![]() .
.
2. По табл. 11.1 определить название поверхности, а по названию –каноническое уравнение поверхности второго порядка.
3. Составить характеристическое уравнение
![]() ,
,
используя коэффициенты, вычисленные в п.1, либо разлагая определитель
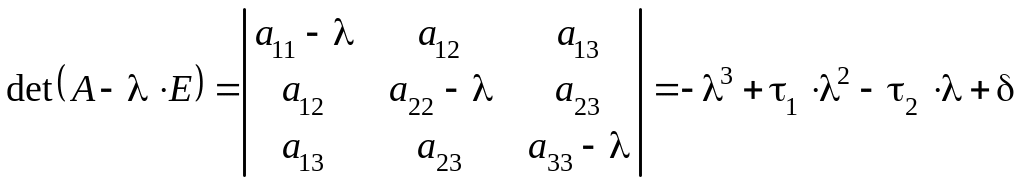 .
.
Найти корни
![]() ,
,![]() ,
,![]() (с учетом кратности) характеристического
уравнения.
(с учетом кратности) характеристического
уравнения.
4. Занумеровать корни , , характеристического уравнения в соответствии с правилами:
а) если поверхность эллиптического
типа, то
![]() ;
;
б) если поверхность гиперболического
типа, то обозначить через
и
корни одного знака так, чтобы
![]() ,
а через
– корень противоположного знака;
,
а через
– корень противоположного знака;
в) если поверхность параболического типа, то
– если нулевой корень двойной, то
![]() и
и
![]() ;
;
– если нулевой корень простой, а
ненулевые корни одного знака, то
![]() и
;
и
;
– если нулевой корень простой, а
ненулевые корни разных знаков, то
![]() и либо
и либо
![]() ,
если
,
если
![]() или
или
![]() ,
либо
,
либо
![]() ,
если
,
если
![]() и
и
![]() .
.
5. Вычислить коэффициенты канонического
уравнения и записать его в канонической
системе координат
![]() :
:
а) для поверхностей эллиптического типа:
(1) – при
![]() – уравнение эллипсоида
– уравнение эллипсоида
![]() с коэффициентами
с коэффициентами
![]() ,
,
![]() ,
,
![]() ;
;
Таблица 11.1. Классификация поверхностей второго порядка
|
Признаки |
Название поверхности |
№ |
||||||
Центральные поверхности |
|
Эллиптический тип |
|
|
Эллипсоид |
1 |
|||
|
Мнимый эллипсоид |
2 |
|||||||
|
Мнимый конус |
3 |
|||||||
Гиперболический тип |
|
|
Однополостный гиперболоид |
4 |
|||||
|
Двуполостный гиперболоид |
5 |
|||||||
|
Конус |
6 |
|||||||
Нецентральные поверхности |
|
Параболический тип |
|
Эллиптический параболоид |
7 |
||||
|
Гиперболический параболоид |
8 |
|||||||
|
|
|
Эллиптический цилиндр |
9 |
|||||
|
Мнимый эллиптический цилиндр |
10 |
|||||||
|
Пара мнимых пересекающихся плоскостей |
11 |
|||||||
|
|
Гиперболический цилиндр |
12 |
||||||
|
Пара пересекающихся плоскостей |
13 |
|||||||
|
|
Параболический цилиндр |
14 |
||||||
|
|
Пара параллельных плоскостей |
15 |
||||||
|
Пара мнимых параллельных плоскостей |
16 |
|||||||
|
Пара совпадающих плоскостей |
17 |
|||||||
(2) при
![]() – уравнение мнимого эллипсоида
– уравнение мнимого эллипсоида
![]() с коэффициентами
с коэффициентами
![]() ,
,
![]() ,
,
![]() ;
;
(3) при
![]() – уравнение мнимого конуса
– уравнение мнимого конуса
![]() с коэффициентами
с коэффициентами
![]() ,
,
![]() ,
,
![]() ;
;
б) для поверхностей гиперболического типа:
(4) при
![]() – уравнение однополостного гиперболоида
– уравнение однополостного гиперболоида
![]() с коэффициентами
,
,
;
с коэффициентами
,
,
;
(5) при
– уравнение двуполостного гиперболоида
![]() с коэффициентами
с коэффициентами
![]() ,
,
![]() ,
,
![]() ;
;
(6) при
– уравнение конуса
![]() с коэффициентами
,
,
;
с коэффициентами
,
,
;
в) для поверхностей параболического типа:
(7) при
– уравнение эллиптического параболоида
![]() с коэффициентами
с коэффициентами
![]() ,
,
![]() ;
;
(8) при
![]() – уравнение гиперболического
параболоида
– уравнение гиперболического
параболоида
![]() с коэффициентами
,
;
с коэффициентами
,
;
(9) при
,
![]() ,
,
![]() – уравнение эллиптического цилиндра
– уравнение эллиптического цилиндра
![]() с коэффициентами
с коэффициентами
![]() ,
,
![]() ;
;
(10) при
,
,
![]() – уравнение мнимого эллиптического
цилиндра
– уравнение мнимого эллиптического
цилиндра
![]() с коэффициентами
с коэффициентами
![]() ,
,
![]() ;
;
(11) при
,
,
![]() – уравнение пары мнимых пересекающихся
плоскостей
– уравнение пары мнимых пересекающихся
плоскостей
![]() с коэффициентами
,
;
с коэффициентами
,
;
(12) при
,
![]() ,
,
![]() – уравнение гиперболического цилиндра
– уравнение гиперболического цилиндра
![]() с коэффициентами
,
;
с коэффициентами
,
;
(13) при
,
,
– уравнение пары пересекающихся
плоскостей
![]() с коэффициентами
с коэффициентами
![]() ,
,
![]() ;
;
(14) при
,
![]() ,
,
![]() – уравнение параболического цилиндра
– уравнение параболического цилиндра
![]() с коэффициентом
с коэффициентом
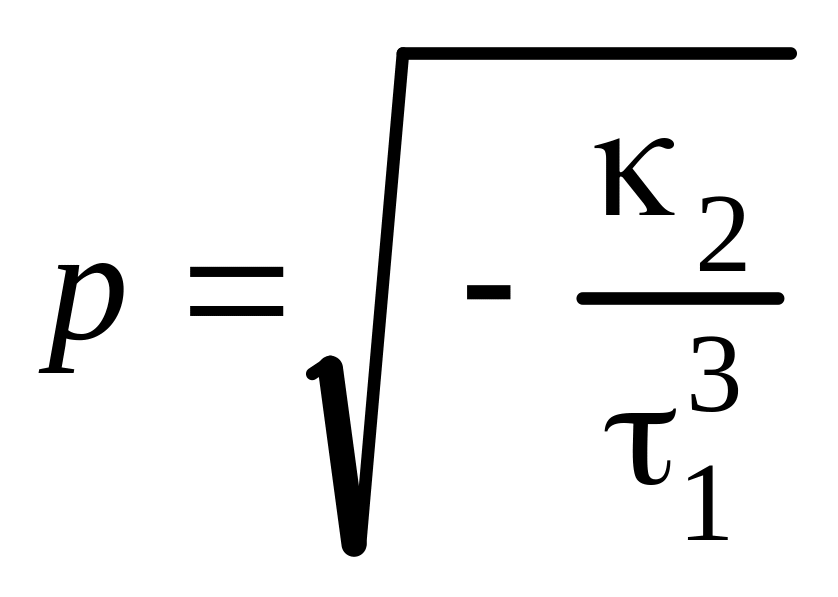 ;
;
(15) при
,
,
,
![]() – уравнение пары параллельных
плоскостей
– уравнение пары параллельных
плоскостей
![]() с коэффициентом
с коэффициентом
![]() ;
;
(16) при
,
,
,
![]() – уравнение пары мнимых параллельных
плоскостей
– уравнение пары мнимых параллельных
плоскостей
![]() с коэффициентом
с коэффициентом
![]() ;
;
(17) при
,
,
,
![]() – уравнение пары совпадающих плоскостей
– уравнение пары совпадающих плоскостей
![]() .
.
Пример 11.10. Определить названия и составить канонические уравнения алгебраических поверхностей второго порядка, заданных в прямоугольной системе координат уравнениями:
а)
![]() ;
;
б)
![]() при
при
![]() ,
,
![]() или
или
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() при
или
при
или
![]() ;
;
ж)
![]() ;
;
з)
![]() ;
;
и)
![]() .
.
а)
Определяем коэффициенты уравнения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1. Вычисляем инварианты:
![]() ,
,
![]() ,
,
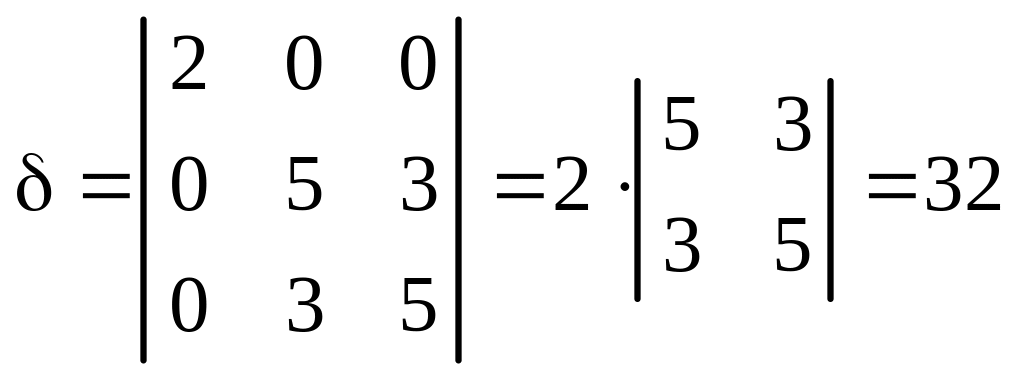 ,
,
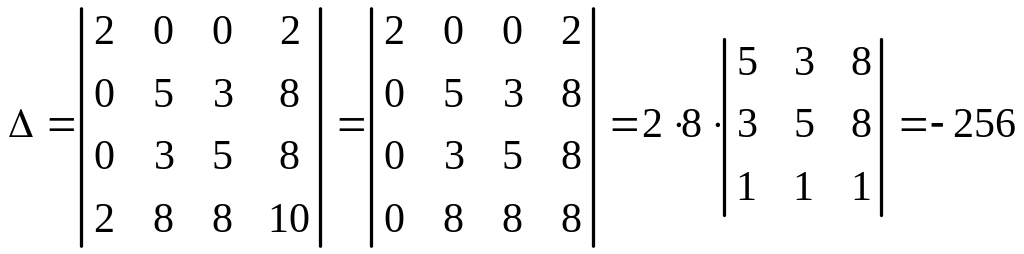 .
.
2. По табл. 11.1 определяем, что уравнение
задает эллипсоид, так как
,
![]() ,
,
![]() .
.
3. Составляем характеристическое уравнение
![]()
и находим его корни:
![]() (двойной корень),
(двойной корень),
![]() (простой корень).
(простой корень).
4. Поскольку поверхность эллиптического
типа, то корни уравнения обозначим
![]() ,
,
![]() ,
чтобы выполнялось условие
,
чтобы выполнялось условие
.
5. Вычисляем коэффициенты канонического уравнения эллипсоида:
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, каноническое уравнение (1) заданной поверхности имеет вид
![]() .
.
б) Определяем коэффициенты уравнения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1. Вычисляем инварианты:
![]() ,
,
![]() ,
,
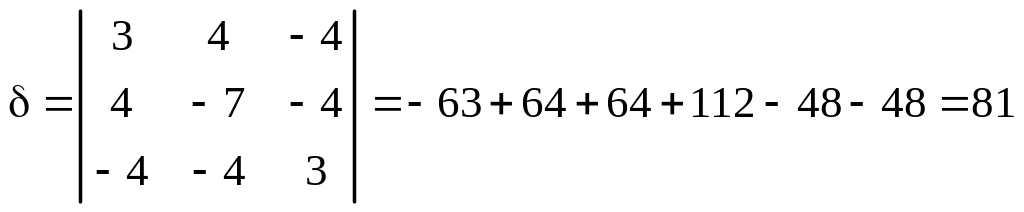 ,
,
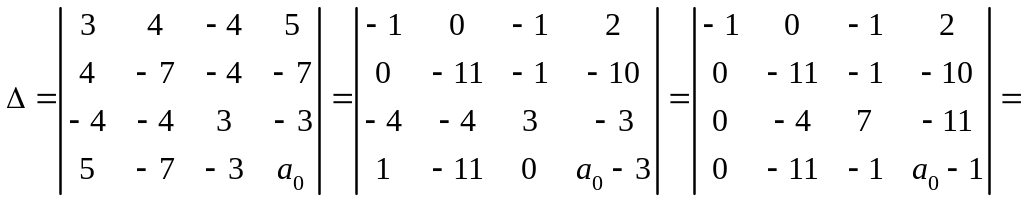
 .
.
2. По табл. 11.1 определяем, что уравнение
задает поверхность гиперболического
типа, так как
![]() .
При
.
При
![]() получаем уравнение однополостного
гиперболоида, так как
получаем уравнение однополостного
гиперболоида, так как
![]() ,
при
,
при
![]() – уравнение конуса, так как
– уравнение конуса, так как
![]() ,
при
,
при
![]() – уравнение двуполостного гиперболоида,
так как
– уравнение двуполостного гиперболоида,
так как
![]() .
.
3. Составляем характеристическое уравнение
![]()
и находим его корни:
![]() ,
,
![]() ,
,
![]() (все корни простые).
(все корни простые).
4. Поскольку поверхность гиперболического
типа, то корни уравнения обозначим
![]() ,
,
![]() ,
т.е.
и
корни одного знака, причем
,
а
,
т.е.
и
корни одного знака, причем
,
а
![]() – корень противоположного знака.
– корень противоположного знака.
5. Вычисляем коэффициенты канонического уравнения:
– однополостного гиперболоида (при
![]()
![]() ):
):
![]() ,
,
![]() ,
,
![]() ,
,
следовательно, каноническое уравнение (4) имеет вид
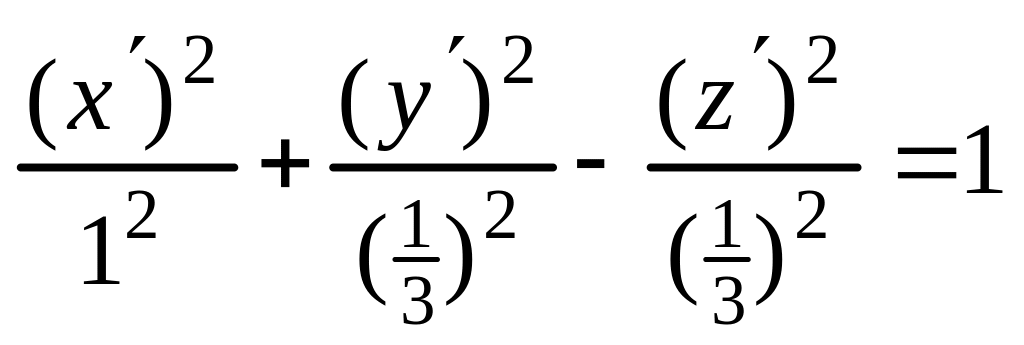 ;
;
– конуса (при ):
![]() ,
,
![]() ,
,
![]() ;
;
следовательно, каноническое уравнение (6) имеет вид
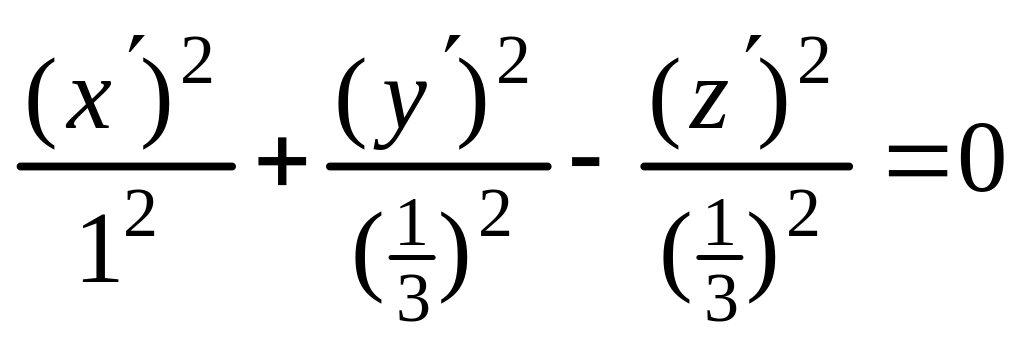 ;
;
– двуполостного гиперболоида (при
![]()
![]() ):
):
![]() ,
,
![]() ,
,
![]() ;
;
следовательно, каноническое уравнение (5) имеет вид
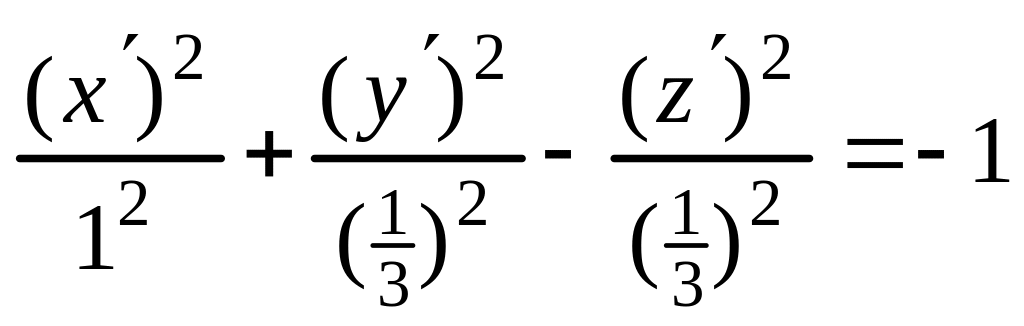 .
.
в) Определяем коэффициенты уравнения:
![]() ,
,
,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1. Вычисляем инварианты:
![]() ,
,
![]() ,
,
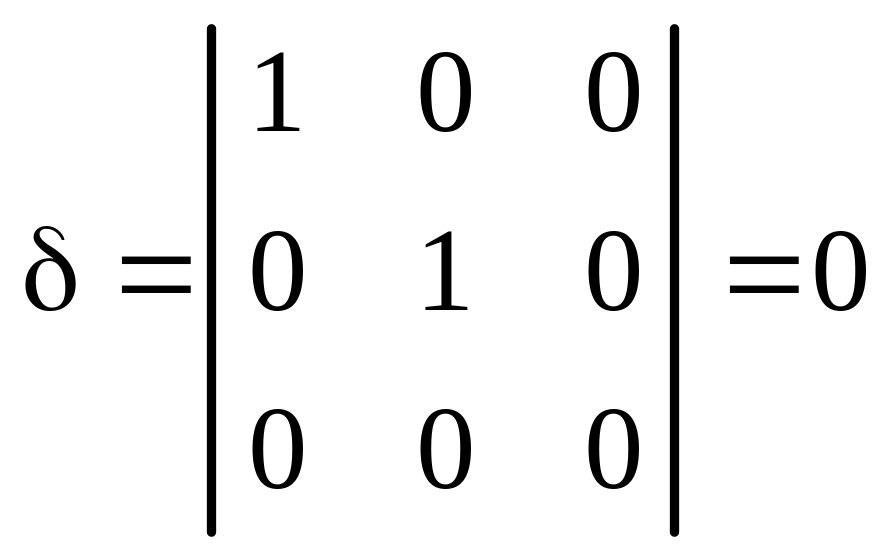 ,
,
 .
.
2. По табл. 11.1 определяем, что уравнение
задает эллиптический параболоид,
так как
![]() ,
.
,
.
3. Составляем характеристическое уравнение
![]()
и находим его корни:
![]() (двойной корень),
(двойной корень),
![]() (простой корень).
(простой корень).
4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:
– единственный нулевой корень; так как
ненулевые корни одного знака, то
![]() ,
чтобы выполнялось условие
.
,
чтобы выполнялось условие
.
5. Вычисляем коэффициенты канонического уравнения эллиптического параболоида:
![]() ,
,
![]() .
.
Таким образом, каноническое уравнение (7) заданной поверхности имеет вид
![]() .
.
г) Определяем коэффициенты уравнения:
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1. Вычисляем инварианты:
![]() ,
,
![]() ,
,
 ,
,

 .
.
2. По табл. 11.1 определяем, что уравнение задает гиперболический параболоид, так как , .
3. Составляем характеристическое
уравнение
![]() и находим его корни:
и находим его корни:
![]() ,
,
,
,
![]() (все корни простые).
(все корни простые).
4. Поскольку поверхность параболического
типа, то корни характеристического
уравнения обозначим следующим образом:
– единственный нулевой корень; так как
ненулевые корни разных знаков и
![]() ,
то
,
то
![]() ,
тогда
,
тогда
![]() .
.
5. Вычисляем коэффициенты канонического уравнения гиперболического параболоида:
![]() ,
,
![]() .
.
Таким образом, каноническое уравнение (8) заданной поверхности имеет вид
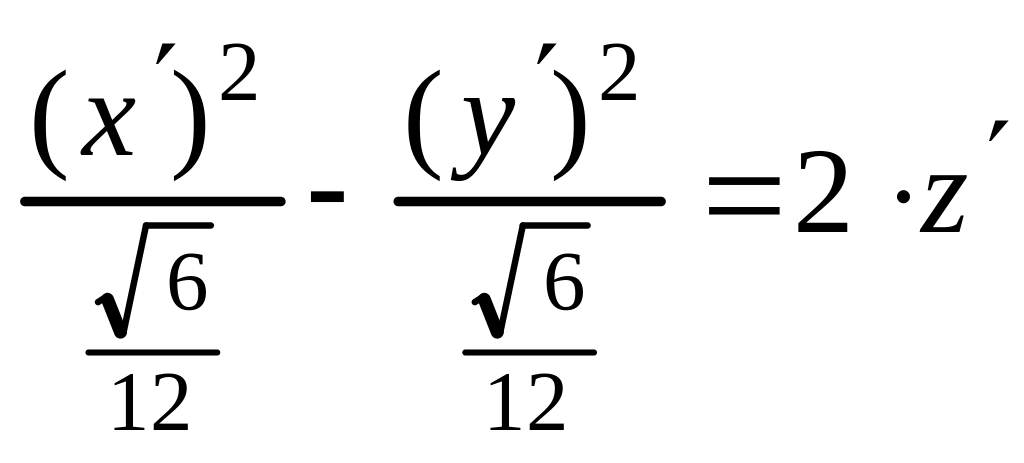 .
.
д) Определяем коэффициенты уравнения:
,
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() .
.
1. Вычисляем инварианты:
![]() ,
,
![]() ,
,
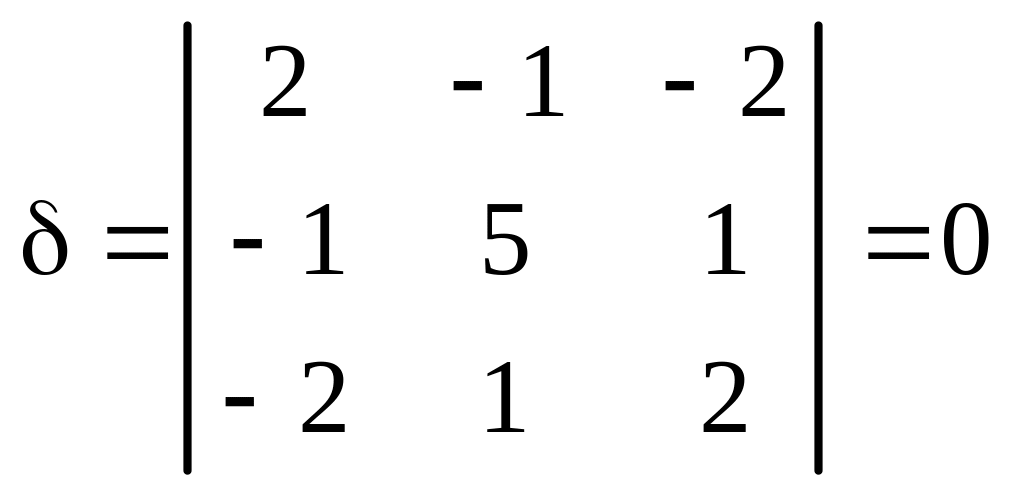 ,
,
 .
.
Так как , то вычисляем семиинвариант:
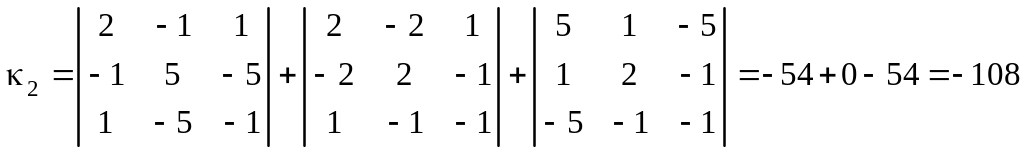 .
.
2. По табл. 11.1 определяем, что уравнение задает эллиптический цилиндр, так как , , , .
3. Составляем характеристическое
уравнение
![]() и находим его корни:
,
и находим его корни:
,
![]() ,
,
![]() (все корни простые).
(все корни простые).
4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:
– единственный нулевой корень; так как
ненулевые корни одного знака, то
![]() ,
,
![]() ,
чтобы выполнялось условие
.
,
чтобы выполнялось условие
.
5. Вычисляем коэффициенты канонического уравнения эллиптического цилиндра:
![]() ,
,
![]() .
.
Таким образом, каноническое уравнение (9) заданной поверхности имеет вид
![]() .
.
е) Определяем коэффициенты уравнения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
,
,
,
![]() ,
,
![]() .
.
1. Вычисляем инварианты:
![]() ,
,
![]() ,
,
 ,
,
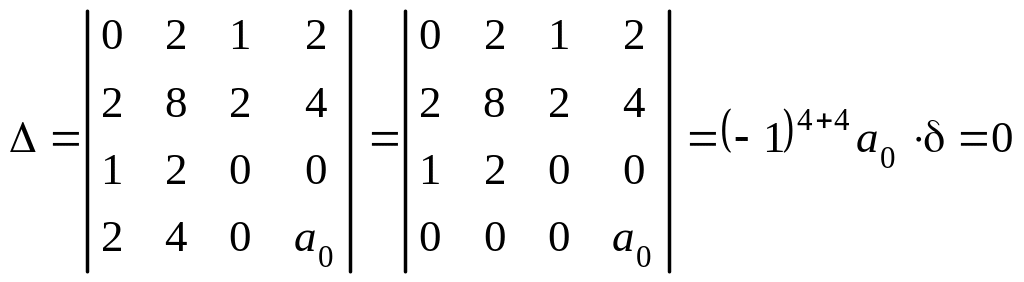 .
.
Так как , то вычисляем семиинвариант:
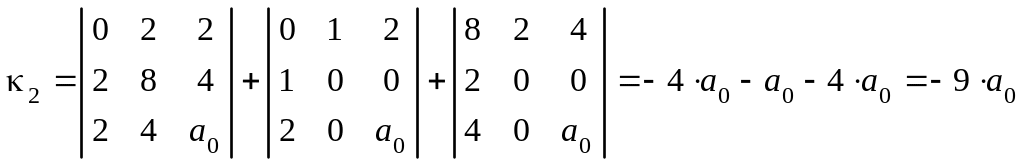 .
.
2. По табл. 11.1 определяем, что уравнение
задает поверхность параболического
типа, так как
.
При
![]() получаем уравнение гиперболического
цилиндра, так как
получаем уравнение гиперболического
цилиндра, так как
![]() ,
,
,
,
![]() ;
при
– уравнение пары пересекающихся
плоскостей, так как
,
,
.
;
при
– уравнение пары пересекающихся
плоскостей, так как
,
,
.
3. Составляем характеристическое уравнение
![]()
и находим его корни:
![]() ,
,
![]() ,
,
![]() (все корни простые).
(все корни простые).
4. Поскольку поверхность параболического
типа, то корни характеристического
уравнения обозначим следующим образом:
– единственный нулевой корень; так как
ненулевые корни разных знаков и
,
то
![]() ,
тогда
,
тогда
![]() (при
имеем
и
(при
имеем
и
![]() ,
а при
имеем
).
,
а при
имеем
).
5. Вычисляем коэффициенты канонического уравнения:
– гиперболического цилиндра (при
![]() ):
):
![]() ,
,
![]() ;
;
следовательно, каноническое уравнение (12) имеет вид
![]() ;
;
– пары пересекающихся плоскостей (при ):
![]() ,
,
![]() ;
;
следовательно, каноническое уравнение (13) имеет вид
 .
.
ж) Определяем коэффициенты уравнения:
![]() ,
,
,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1. Вычисляем инварианты:
![]() ,
,
![]() ,
,
 ,
,
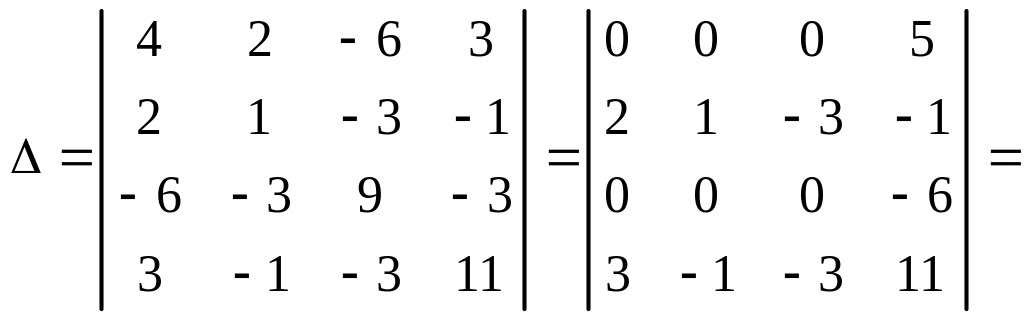
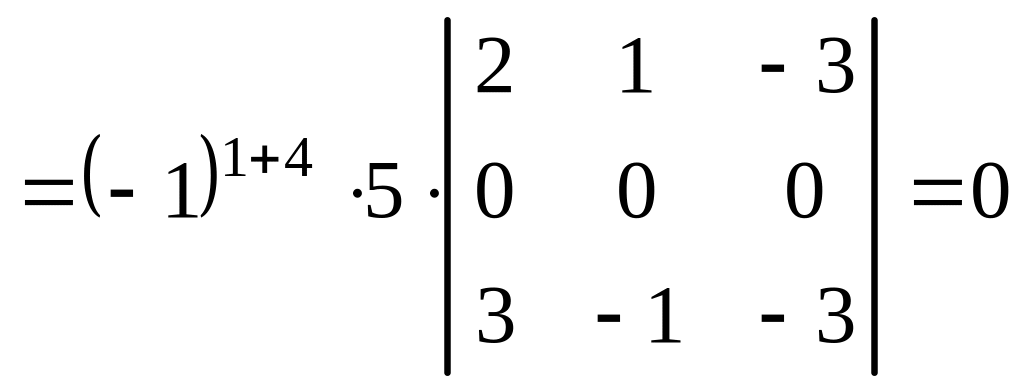 .
.
Так как
![]() ,
то вычисляем
,
то вычисляем
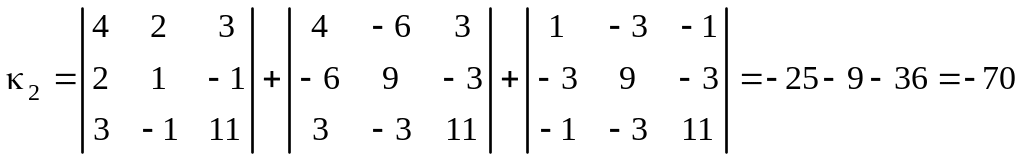 .
.
2. По табл. 11.1 определяем, что уравнение
задает параболический цилиндр, так
как
,
,
![]() ,
.
,
.
3. Составляем характеристическое
уравнение
![]() и находим его корни:
(двойной корень),
и находим его корни:
(двойной корень),![]() (простой корень).
(простой корень).
4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:
![]() – двойной нулевой корень, а
– двойной нулевой корень, а
![]() – ненулевой корень.
– ненулевой корень.
5. Вычисляем коэффициент канонического уравнения параболического цилиндра:
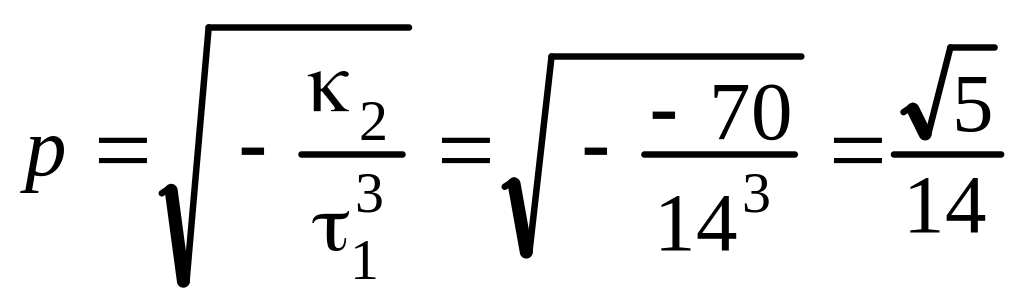 .
.
Таким образом, каноническое уравнение (14) заданной поверхности имеет вид
![]() .
.
з) Определяем коэффициенты уравнения:
,
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
.
,
,
.
1. Вычисляем инварианты:
![]() ,
,
![]() ,
,
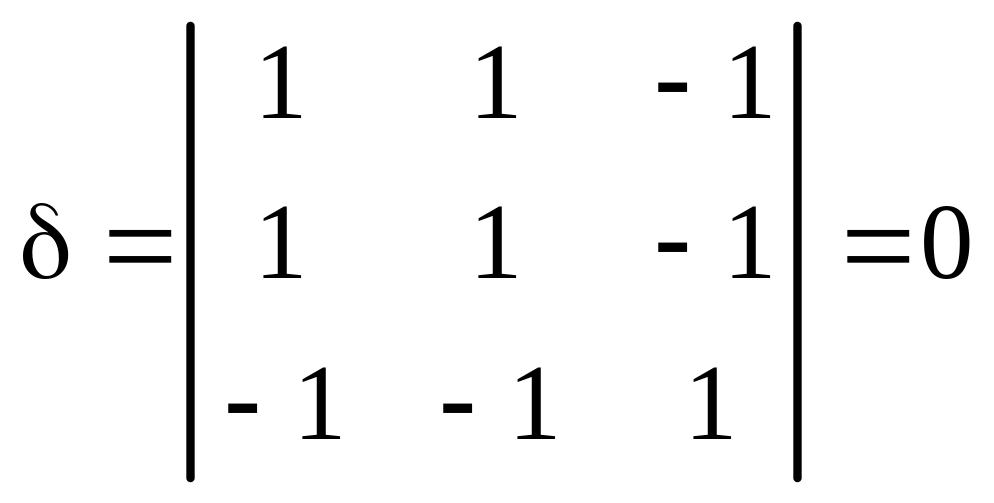 ,
,
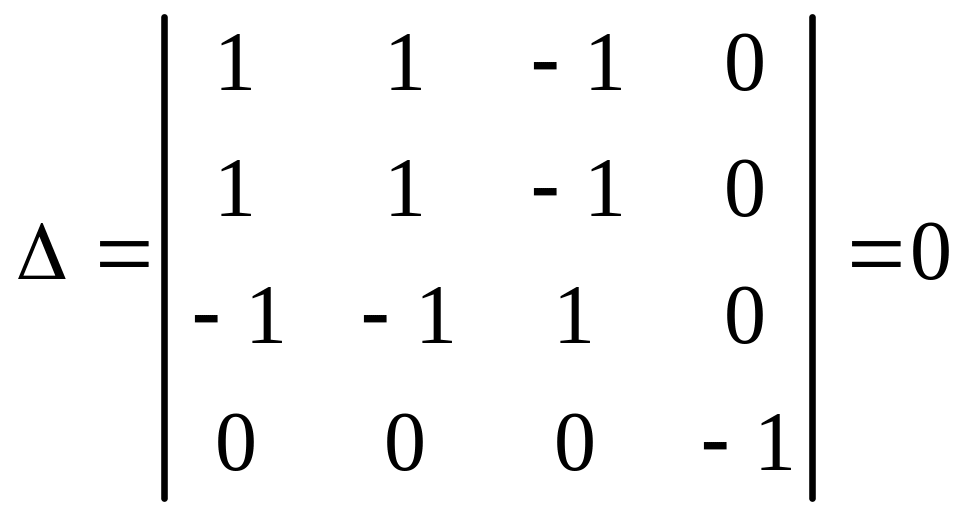 .
.
Так как , то вычисляем
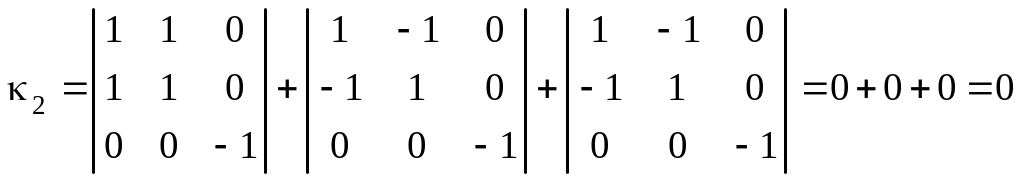 .
.
Так как и , то вычисляем
![]() .
.
2. По табл. 11.1 определяем, что уравнение задает пару параллельных плоскостей, так как , , , , .
3. Составляем характеристическое
уравнение
![]() и находим его корни:
(двойной корень),
и находим его корни:
(двойной корень),
![]() (простой корень).
(простой корень).
4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:
– двойной нулевой корень, а
![]() – ненулевой корень.
– ненулевой корень.
5. Вычисляем коэффициент канонического уравнения пары параллельных плоскостей:
![]() .
.
Таким образом, каноническое уравнение (15) заданной поверхности имеет вид
![]() .
.
и) Определяем коэффициенты уравнения:
,
,
,
,
,
,
![]() ,
,
,
.
,
,
,
.
1. Вычисляем инварианты: ,
![]() ,
,
![]() ,
,
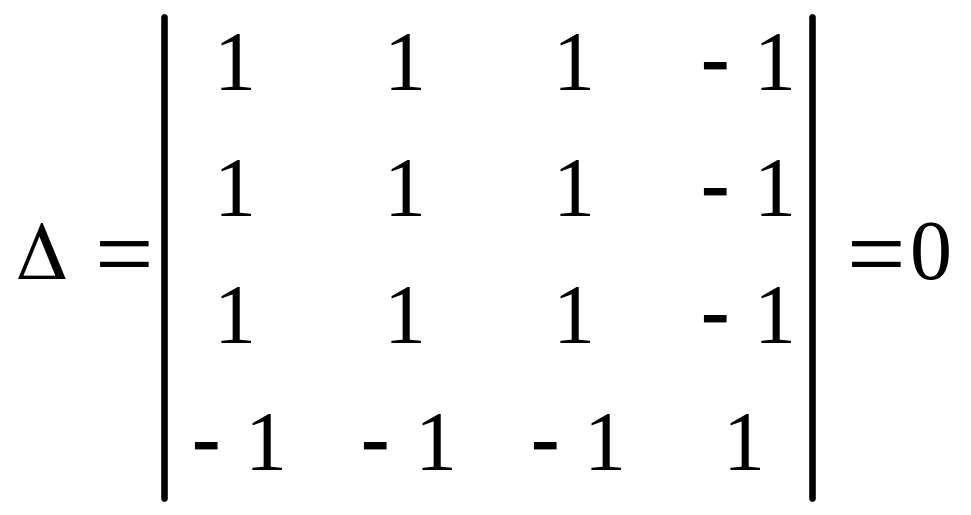 .
.
Так как , то вычисляем
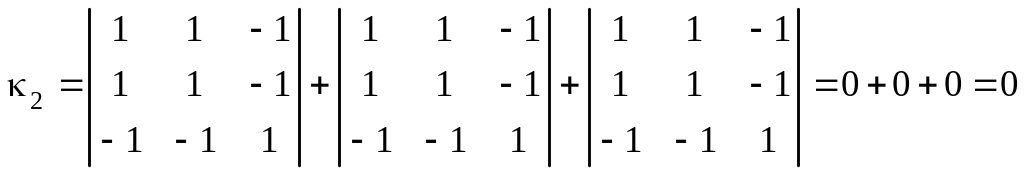 .
.
Так как и , то вычисляем
![]() .
.
2. По табл. 11.1 определяем, что уравнение задает пару совпадающих плоскостей, так как , , , , .
3. Составляем характеристическое уравнение и находим его корни: (двойной корень), (простой корень).
4. Поскольку поверхность параболического типа, то корни уравнения обозначим следующим образом: – двойной нулевой корень, а – ненулевой корень.
5. Записываем каноническое уравнение (17) пары совпадающих плоскостей:
.
