
I вариант
Задание 1. Положите на парту 8 кружков. Отодвиньте 5 кружков. Сколько кружков осталось?
Дети записывают: 8—5 = 3.
Задание 2. Как называются числа 8, 5, 3 в этом примере? (Дети вспоминают термины, учитель помогает им.)
Задание 3. Покажите кружки, число которых равно вычитаемому (дети показывают 5 кружков), разности (показывают 3 кружка).
Задание 4. Придвиньте снова 3 кружка к 5. Сколько получилось?
Учитель еще раз обращает внимание на ту операцию, которую они выполняли: “Сложили вычитаемое 5 с разностью 3 и получили чменьшаемое 8”.
Задание 5. На доске два примера: 8—5 = 3, 3 + 5 = 8. Сравните эти примеры. Как получили уменьшаемое?
Учащиеся должны повторить ту фразу, которую только что произнес учитель. Большинство учеников все-таки отвечает: “3 + 5 = 8”. Учитель еще раз повторяет: “К разности прибавили вычитаемое, получили уменьшаемое”.
Приведенные пять заданий повторяются в той же последовательности еще два раза с другим числом предметов: 6—2-4, 4—3=1.
Задание 6. Давайте еще раз убедимся, что если к вычитаемому прибавим разность, то получим уменьшаемое.
Учащиеся решают различные примеры на вычитание, находят разность, затем к разности прибавляют вычитаемое, получают уменьшаемое.
Изложенную последовательность заданий можно охарактеризовать следующим образом.
Это целенаправленное подведение учащихся к обобщению: “Если к разности прибавим вычитаемое, то получим уменьшаемое”. Эту характеристику можно было бы признать положительной, если бы целенаправленность не выражалась в таком узком и однообразном подходе к осознанию взаимосвязи между компонентами и результатом вычитания, что работа превратилась фактически в заучивание и тренировку.
Можно признать положительным то, что учитель обращается к наглядному материалу, но, к сожалению, метод изложения нового материала аналогичен методу изложения темы “Нахождение неизвестного слагаемого”. Между тем данная тема изучается значительно позже, а потому было бы естественным ожидать какого-то изменения в методике рассмотрения сходного вопроса.
Анализируя задания, можно констатировать, что они не побуждают учеников устанавливать взаимосвязи с ранее изученным материалом, хотя такая возможность имеется.
Задания по степени сложности одинаковы. От учеников каждый раз требуется лишь проверить, действительно ли то, что если к разности прибавить вычитаемое, то получим уменьшаемое.
II вариант
Прежде чем переходить к изложению заданий на данном уроке, остановим внимание на теме, которая изучалась в первой четверти: “Вычесть 5, 6, 7, 8, 9”. Для того чтобы из 8 вычесть 6, дети должны были рассуждать так: “8 — это сумма чисел 2 и 6. Если из суммы двух слагаемых вычесть одно из них, то получится другое”. Учащиеся строили рассуждения, не оперируя терминами “уменьшаемое”, “вычитаемое”, “разность”, но каждый раз они убеждались, что уменьшаемое — это сумма двух чисел (разности и вычитаемого). Почему же надо пренебрегать уже имеющимися знаниями? Кроме того, к моменту изучения темы учащиеся уже умеют записывать равенства (примеры), содержащие неизвестное.
Исходя из сказанного, задания предлагаются в следующей последовательности:
Задание 1. Записать: из неизвестного числа вычесть 7, получим 3.
Задание сразу вводит учащихся в курс изучаемого вопроса, в
то же время оно не представляет сложности для ученика, так как прямо указывает на то арифметическое действие, которым связаны неизвестное и данные числа. (Дети записывают: х—7 = 3.)
Задание 2. Чему равен x?
Дети быстро дают ответ: х=10 — и обосновывают ответ так: “Потому что 10—3 = 7”.
Не следует огорчаться, что в качестве обоснования не было сказано: “Потому что 3 + 7=10”. Ведь именно такая цель и поставлена на уроке, и, чтобы достигнуть ее, учитель подбирает соответствующую серию заданий.
Задание 3. 9—3 = 6
х—3 = 5
Сравните уменьшаемые, вычитаемые, разности.
Опишем небольшой эпизод из урока.
— Верно ли будет, если во втором примере подставить вместо х число 9? (Нет. Потому что из 9—3; будет 6, а у нас 5.)
— Хорошо. Ты подставила вместо х число 9 и убедилась, что запись неверная. А кто по-другому может объяснить? (9 — это сумма чисел 6 и 3, а у нас 5 и 3, это 8, х = 8.)
— Давайте еще проследим, как же" мы нашли неизвестное число. (3 + 5 = 8. А можно по-другому. В первом и во втором примерах вычитаем 3. В первом получили 6, а во втором — 5. В первом вычитали из 9, значит, во втором будем вычитать из другого числа. Во втором примере осталось меньше, значит, и число было меньше. 8 подходит.)
Такие рассуждения нельзя оставить без одобрения. Очень важно, чтобы задание давало возможность в большей степени раскрыться и проявить инициативу всем ученикам. Итак, задание выполнено. Не только с целью сформулировать правило, но и для того, чтобы мысль ученика работала, чтобы он постепенно подготавливался к пониманию взаимосвязи между компонентами и результатом вычитания.
Задание 4. Прочитайте числа: 10, 2, 12; 8, 10, 18. Запишите с помощью данных трех чисел примеры на вычитание.
Учащиеся записывают:
12—2=10 18—10 = 8 12—10 = 2 18—8=10
Учитель спрашивает: “Заметили ли вы, какое из трех данных чисел в каждом случае брали в качестве уменьшаемого?” (Самое большое из трех данных чисел.)
Если учащиеся затрудняются ответить, можно предложить сравнить числа между собой, выяснить, какое самое большое, и после этого вернуться к поставленному вопросу.
Задание 5. Задание по форме аналогично 4-му заданию, только даны другие числа: 11, 1, 9; 10, 18, 7.
Выполняя его, учащиеся начинают понимать связь между компонентами и результатом действия вычитания.
Они хором заявляют, что с такими числами нельзя составить примеры на вычитание. Объясняют по-разному: “Потому что 11—1 = 10, а у нас 9, из 18—10 = 8, а у нас 7; потому что из 11 — 1 не получится 9, 9+1 = 10”. Был даже такой ответ: “Можно записать так: 11—1>9”. Учитель подтверждает, что пример записать нельзя, и спрашивает, какое число они все-таки пытались взять в качестве уменьшаемого. (Большее: 11, 10.) Какими же должны быть уменьшаемые, чтобы можно было составить примеры? (В первом случае 10, так как 9+1 = 10, во втором 17, так как 10 + 7=17.)
Задание 6. Я задумала число, прибавила к нему 5, получила 16. Найдите неизвестное число. (* + 5=16, я =16—5, х=11.)
Задание 7. Я задумала число, вычла из него 5, получила 11. Запишите пример (равенство), обозначая неизвестное буквой v. Найдите неизвестное число.
Два аналогичных по форме задания: одно на нахождение неизвестного слагаемого, другое на нахождение неизвестного уменьшаемого — даются с целью, чтобы дети самостоятельно сделали запись нахождения неизвестного уменьшаемого. Несмотря на то что детям не давали образца, они справились с заданием.
После этого предлагалось несколько заданий, в которых фигурировала термины “уменьшаемое”, “вычитаемое”, “разность”. Например:
Задание 8. Уменьшаемое — неизвестное число, вычитаемое 25, разность 4. Найдите неизвестное уменьшаемое.
Задание 9. Попробуйте сформулировать правило, как найти неизвестное уменьшаемое.
Задание 10. Выпишите в разные столбики примеры, которые связаны между собой. Объясните эту взаимосвязь.
12—2=10 12—10=2
15—1 = 14 10 + 2 = 12
10—8 = 2 8 + 2=10
10—2 = 8 15—14=1
14+1 = 15
Задание вызывает у учащихся большую активность. Каждый по-своему пытастся сгруппировать данные примеры. Само слово “взаимосвязаны” еще не совсем понятно ученикам, но выполнение задания как раз и способствует осознанию этого термина. Например, учащиеся делают попытку сгруппировать примеры следующим образом:
12—2=10 14 + 1 = 15 15—1 = 14 10 + 2 = 12
10—8 = 2 8 + 2=10
10—2 = 8
12—10 = 2
15—14-1
обосновывая ее тем, что в одних примерах знак “плюс”, в других— “минус”. Учащиеся нашли сходство в одинаковых арифметических действиях. Но разве примеры 14+1 = 15 и 10 + 2=12 связаны как-то между собой? Здесь разные суммы, разные слагаемые.
Более наблюдательные ученики замечают, что в некоторых примерах на сложение и вычитание фигурируют одни и те же числа:
14+1 = 15 15—1 = 14 15—14=1
Объясняют: эти примеры связаны между собой. Сложили 14 и 1, получили 15. Из 15 вычли 1, получили первое слагаемое, из 15 вычли 14, получили второе слагаемое. Примеры на сложение и вычитание составлены из трех чисел: 15, 14, 1.
Конечно, можно спорить, стоит ли выслушивать такие расплывчатые рассуждения, ведь это занимает много времени. Конечно, это так, но, с другой стороны, такие задания, несомненно, способствуют развитию наблюдательности, расширяют математический кругозор и, кроме того, проверяют, насколько учащиеся осознают взаимосвязь компонентов и результатов действий.
Задание 11. Как можно проверить сложением, верно ли найдена разность 29—7 = 22?
Таким образом, принцип подбора заданий ко второму варианту урока существенно отличается от принципа подбора заданий к первому варианту. Во втором варианте реализованы все принципы подбора заданий, руководство которыми обеспечивает их развивающую функцию, — это сочетание воспроизводящей деятельности ученика с наблюдением, анализом, сравнением, взаимосвязь каждого последующего задания с предыдущим, постепенное усложнение заданий, а самое главное, что при подборе заданий для второго варианта уроков устанавливаются различные связи с ранее изученными вопросами курса и изучаемый вопрос рассматривается в различных аспектах. Возможность осуществления такого подхода во многом определяется тем, какое место в процессе обучения отводится повторению учебного материала.
Остановимся на этом вопросе более подробно.
На каждом уроке учитель отводит специальное время повторению ранее пройденного материала и после этого приступает к изучению новой темы. Часто учитель прибегает к так называемому закреплению, В этом случае повторению пройденного материала отводится 2—3 урока, на которых дети выполняют различные задания, применяя те знания, которые они усвоили на предшествующих уроках, при этом задания часто дублируются и в них не вносится элементов новизны. Когда же, по мнению учителя, основная масса учащихся справляется с предлагаемыми заданиями, учитель переходит к объяснению нового материала. Стараясь установить взаимосвязь ранее изученного с новым материалом, учитель, прежде чем перейти к новому вопросу, повторяет тот материал, который необходим для изучения новой темы, но потом
зачастую полностью переключается на новый вопрос, и дальнейшая связь нового материала с ранее изученным пропадает или осуществляется однобоко.
Такое разграничение повторения и усвоения новых знаний, безусловно, нельзя признать рациональным. Ведь сознательное и прочное усвоение знаний — это прежде всего их взаимосвязь, т. е. органическое включение ранее усвоенных знаний в процесс овладения новыми знаниями.
Поэтому перед каждым учителем стоит задача осуществления продуманного и творческого подхода к вопросу повторения учебного материала, нахождения наиболее эффективных способов и приемов.
Покажем, как возможно осуществить более тесную взаимосвязь нового материала с ранее изученными вопросами, что создает условия для большей самостоятельности учащихся в овладении новыми знаниями и способствует расширению их математического кругозора.
Возможность такого подхода мы рассмотрим во II классе на примере изучения темы “Тысяча”.
Большое значение для изучения устной и письменной нумерации трехзначных чисел имеет осознание детьми различия между такими понятиями, как “цифра” и “число”. При изучении однозначных и двузначных чисел не всегда уделяется достаточное внимание дифференцированию этих понятий. Дети часто употребляют в своей речи слова “цифра”, “число”, но делают это не всегда верно.
Например, на доске написано: 52. Учитель проводит беседу
— Что написано на доске — цифра или число? (Дети отвечают: “Число. Цифра всегда одна, а число состоит из десятков и единиц. Число 52 записано с помощью цифр 5 и 2”.)
— Вы говорите, что число обязательно состоит из десятков и единиц. А какие числа мы изучали в начале I класса? (Однозначные числа. 52 — это двузначное число, оно записано двумя цифрами. Я знаю 10 цифр — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Чисел бесконечно много, все назвать нельзя. Цифры — это значки, которыми мы записываем числа.)
Дети обобщают сказанное о цифре и числе.
Таким образом, в процессе беседы проходит повторение ранее усвоенных знаний.
Учитель предлагает детям вопрос: “Сколько чисел можно записать, используя только одну цифру 4?” Дети предлагают: 4, 44, 444 и даже 4444, только не могут прочитать это число, но в данном случае не это является целью. Уже сама попытка записи четырехзначного числа с помощью одной цифры как бы конкретизирует для второклассников понимание такого сложного вопроса, как бесконечность числового ряда.
Далее учитель выясняет:
— В чем отличие и в чем сходство чисел 35 и 53? (Они оба написаны с помощью цифр 3 и 5, но в первом случае цифра 3
стоит в разряде десятков, а во втором — эта же цифра стоит в разряде единиц и т. д.)
— А какие числа можно записать с помощью цифр 4 и 0? (Дети предлагают различные варианты: 40, 400, 44 и т. д.)
— А можно ли записать такое число: 04? (Нет. Если стоит 0, значит, в разряде десятков нет десятков, а есть только 4 единицы, поэтому надо писать 4.) Запишите любое число, в котором два разряда. (Дети предлагают самые различные двузначные числа )
— Какое самое большое двузначное число? (99.) А какое число следует дальше? (100.)
— Можно ли назвать это число двузначным? (Нет, здесь три цифры, значит, оно трехзначное.)
— Как вы думаете, какой новый разряд появляется в трехзначном числе?
Проведенная беседа и знакомое детям число 100 привело к самостоятельному выводу о появлении третьего разряда — разряда сотен. Безусловно, введение разряда сотен еще не гарантирует осознание сущности данного разряда детьми, а поэтому не исключает дальнейших заданий, которые дети выполняют на наглядном материале. Но изложенный подход дает возможность повторить целый ряд вопросов, привести их в систему и подвести детей к знакомству с новым для них понятием трехзначного числа.
Приведем ряд заданий, в которых осуществляется связь с ранее изученными вопросами.
1. Чем похожи и чем отличаются друг от друга числа каждой пары?
1 и 101 10 и 110
2 и 102 И и 111
3 и 103 12 и 112
Выясняя сходство и различие данных пар чисел, дети оперируют понятиями: цифра, число, однозначное, двузначное, трехзначное число, первый разряд, второй разряд, третий разряд — и помимо этого наблюдают, сравнивают, анализируют.
2. Запишите все трехзначные числа, у которых в разряде единиц стоит цифра 8, а в разряде сотен цифра 1. На сколько единиц каждое следующее число в полученном ряду больше предыдущего?
3. Выпишите все круглые числа, у которых в разряде сотен стоит цифра 3. Чему равна разность последующего и предыдущего чисел в полученном ряду чисел?
4. Запишите трехзначное число, в котором число сотен равно 2, число десятков в три раза больше числа сотен, а число единиц равно сумме числа десятков и числа сотен.
При выполнении данного задания дети повторяют увеличение числа в несколько раз и на несколько единиц, результатом же является запись трехзначного числа. Другими словами, новый материал как бы пронизывается знаниями, которыми располагают дети. Учителя сами могут составить различные задания, аналогичные приведенному. Остановимся еще на одном задании данного вида, способ выполнения которого носит несколько иной характер.
5. Запишите число, в котором число десятков на 2 больше числа сотен, а число единиц равно сумме числа десятков и числа сотен.
Если предыдущее задание выполнялось однозначно, то выполнение данного задания имеет варианты. В зависимости от того числа сотен, которое зададут дети, будут строиться их дальнейшие рассуждения. Более того, они столкнутся при выполнении задания как бы с областью тех допустимых значений, которыми можно задавать число сотен. Так, если они примут число сотен, равное 4, то выполнение условия задания будет невозможно. Задания такого характера нацеливают на тщательный анализ условия, что способствует более осознанному его выполнению.
Можно предложить интересные задания на группировку, выполнение которых также потребует привлечения ранее изученных вопросов.
1. Разбейте данные числа на две группы так, чтобы в каждой группе были числа, похожие между собой одним признаком: 345, 54, 78, 591, 84, 765, 384, 91. (Дети выделяют две группы: в одну из них входят двузначные числа, в другую — трехзначные).
2. Разбейте данные числа на две группы так, чтобы в каждую иэ них входили числа, похожие между собой двумя признаками: 570, 873, 343, 520, 740, “10, 983, 753. (Дети выделяют две группы чисел: в первую входят трехзначные числа, оканчивающиеся нулем, во вторую — трехзначные числа, оканчивающиеся цифрой 3.) Ценность данного задания заключается не только в повторении изученных понятий, но и в том, что процесс его выполнения требует различных видов интеллектуальной деятельности — тщательного анализа каждою предложенного числа, сопоставления чисел, наблюдательности и сообразительности. Если класс справляется с такого вида заданиями, то задание можно еще усложнить.
3. На сколько групп можно разбить данные числа, чтобы я каждой из них были числа, похожие между собой двумя признаками: 20, 487, 75, 840, 520, 727, 60, 45, 85, 680, 937, 80?
Дети должны сами определить число возможных группировок. (Один из вариантов: 1-я группа — двузначные числа, оканчивающиеся нулем, 2-я группа — трехзначные числа, оканчивающиеся нулем, 3-я группа — двузначные числа, оканчивающиеся цифрой 1 5, 4-я группа — трехзначные числа, оканчивающиеся цифрой 7.)
Задания на группировку не только интересный прием повторения, но и способ развития различных интеллектуальных умений.
С целью повторения закономерности построения натурального ряда чисел можно предложить задания:
1.
200 201 202 203 204
205 206 207 208 209
210 211 212 213 214
215 216 217 218 219
Сумма чисел первого столбика равна 830. Догадайтесь, как можно быстрее найти сумму в других столбиках. Какую закономерность вы наблюдаете во всех данных примерах?
2. 376—375
375—374 374—373 373—372 372—371 и т. д.
Чем похожи данные примеры? Какой можно сделать вывод? (Разность предыдущего и последующего числа равна 1.) Подтвердите вывод на примере однозначных и двузначных чисел.
Повторяя решение уравнений при изучении трехзначных- чисел, помимо заданий, в которых нужно найти неизвестный компонент, пользуясь правилом (в данном случае значения компонентов вместо двузначных и однозначных становятся трехзначными), можно предложить ряд заданий, способствующих расширению математического кругозора учащихся.
1. Найдите неизвестное слагаемое: x + 384 = 9 + 384.
При нахождении неизвестного в данном уравнении ученики могут не пользоваться правилом нахождения неизвестного слагаемого, а прибегнуть к сравнению выражений, стоящих в левой и правой частях.
Найдите неизвестное слагаемое: 932 + 384 = x + 932.
Дети опять прибегают к сравнению выражений, стоящих з левой и правой частях равенства, ссылаясь на переместительный закон сложения, делают вывод относительно значения неизвестного,
2. Решите уравнения: x + 20 + 9 = 829
300+x + 5 = 375
Знание разрядного состава трехзначного числа позволяет также найти неизвестное слагаемое, не прибегая к правилу нахождения неизвестного слагаемого. Дети подмечают, что выражение, записанное слева, представляет сумму разрядных слагаемых числа, записанных в правой части уравнения. Таким образом, знакомый для учеников вопрос нахождения неизвестного слагаемого осмысливается под углом зрения нового материала.
3. Внимательно рассмотрите данные уравнения, сравните в каждом из них сумму и известное слагаемое. Что вы заметили?
356+х = 359 356 + x = 386 356+х = 656
Дети прежде всего указывают на то, что первые слагаемые во всех уравнениях одинаковые. Учитель нацеливает детей на сравнение первого слагаемого и суммы. Дети отмечают, что в первом уравнении изменилась цифра, стоящая в разряде единиц, во втором— цифра, стоящая в разряде десятков, в третьем — цифра, стоящая в разряде сотен. Осознание разрядного состава трехзначного числа позволяет сделать вывод о значении неизвестного слагаемого.
После того как дети перейдут к сложению и вычитанию трехзначных чисел, можно предложить задания такого типа:
1. На сколько нужно уменьшить число 378, чтобы: а) в разряде десятков иметь цифру 2; б) в разряде сотен иметь цифру 1; в) в разряде единиц иметь цифру 5?
Задания, которые имеют несколько вариантов решения, лучше давать на дом.
Вот примеры таких заданий.
2. Запишите трехзначные числа, в которых разность числа единиц и числа десятков равна 3 (число сотен в данном случае задается произвольно).
3. Запишите трехзначные числа, в которых сумма числа сотен, десятков и единиц равна 9.
Учитель сам может составить много аналогичных заданий.
Органическое включение ранее приобретенных знаний в процесс овладения новым материалом и реализацию данного подхода в учебных заданиях можно конкретизировать и на примере изучения других вопросов курса.
Рассмотрим изучение таких тем курса математики начальных классов, как “Умножение и деление на 10, 100, 1000 ...” и “Умножение и деление чисел, оканчивающихся нулями”. Эти вопросы выбраны не случайно: методика их изучения мало изложена в методической литературе. Вероятно, это вызвано тем, что усвоение этих вопросов не представляет особой трудности для учащихся. Тем не менее сознательное усвоение вычислительных приемов умножения и деления на 10, 100, 1000 и на числа, оканчивающиеся нулями, имеет важное значение для последующего изучения, например, таких вопросов, как умножение и деление десятичных дробен.
Курс математики начальных классов построен таким образом, что эти вопросы изучаются не сразу, а в несколько этапов. Хорошо представляя взаимосвязь этих этапов, учитель сможет совершенствовать и углублять знания учащихся на каждом из них.
Умножение и деление на 10 рассматривается во II классе до изучения табличных случаев умножения и деления. В учебнике приведено задание, в процессе выполнения которого учащиеся знакомятся со случаем умножения и деления на 10. Рассмотрим его.
— Продолжи столбики примеров. Рассуждай так: чтобы умножить 10 на 2, надо 1 десяток умножить на 2, получится 2 десятка или 20. Если 10-2 = 20, то 2*10 = 20 и 20:2=10, 20:10 = 2, 10*3= ..., то ... и ........ В первом столбике последним должен быть пример 10*10.
Для выполнения этого задания необходимо использовать знание переместительного свойства умножения, взаимосвязь умножения и
деления (нахождение неизвестного множителя), а также то, что 10 единиц составляют 1 десяток. Все эти вопросы учитель предварительно повторяет, предлагая учащимся различные устные упражнения в начале урока. Приступая к изучению нового вопроса, учитель чаще всего обращается к приведенному заданию.
Какой метод изучения использует при этом учитель?
В задании дается образец решения одного примера, затем в соответствии с данным образцом учащиеся выполняют решение аналогичных примеров. Следовательно, используется объяснительно-иллюстративный метод, и деятельность учеников носит репродуктивный характер. Учащиеся запоминают способ действия в процессе его однотипного применения. Казалось бы, цель достигнута, но деятельность ученика однообразна, репродуктивна, не побуждает его к поиску и не способствует установлению различных связей. В результате использования объяснительно-иллюстративного метода в данном случае снижается не только познавательная активность учащихся, но и усвоение нового вопроса, которое часто носит формальный характер.
Покажем возможность использования метода беседы и практической работы учащихся при выполнении различных заданий при изучении темы “Умножение и деление на 10”.
1. Сравни числа каждого ряда. В чем их сходство, в чем различие?
1 2 3 4 5 6 7 8 9
10 20 30 40 50 60 70 80 90
Сколько десятков содержит каждое из чисел второго ряда?
При выполнении данного задания учащиеся повторяют поместное значение цифр, их внимание обращается на то, что цифра, стоящая на втором месте справа, означает число десятков.
Вопрос, сколько десятков содержит каждое число второго разряда, фиксирует внимание учащихся на записи с помощью цифр таких чисел, как 2 десятка, 3 десятка и т. д.
Опираясь на ответ, данный учащимися, учитель может провести математический диктант.
— Запиши в тетрадь выражения: один десяток умножь на 2. Сосчитай, сколько десятков получится, и запиши ответ. Один десяток умножь на 3, на 4, на 5.
В тетрадях учащихся появляются записи: 10-2 = 20, 10-3 = 30, 10-4 = 40, 10-5=50.
Используя математический диктант, учитель как бы подсказал способ умножения, но тем не менее доля самостоятельной деятельности учащихся присутствует: самостоятельно они записывают данные выражения и ответ с помощью цифр без показа образца записи.
Вопросы, сколько раз нужно взять по 10, чтобы получить числа 60, 70, 80, 90, 100, и как это записать, позволяют учащимся рассмотреть данные числа с точки зрения сути действия умножения, к изучению которого они приступили во II классе, т. е. если
в задании выше они переводили словесную формулировку на язык знаков, то в следующем задании они осмысливают эту запись.
2. Составь самостоятельно из каждого примера на умножение два примера на деление.
При выполнении задания учащиеся используют свои знания о нахождении неизвестного множителя. Учитель в случае необходимости может поставить наводящие вопросы.
3. Сравни пары примеров. Что ты заметил?
7-1 8-1 4-1 7-10 8-10 4-10
При выполнении задания сопоставляются случаи умножения на 1 (ранее изученные) и случаи умножения на 10. Повторяется правило умножения на 1 (при умножении на 1 получаем то число, которое умножаем) и обобщается новый способ — при умножении на 10 получаем число, которое содержит столько десятков, сколько единиц в первом множителе.
4. Сравни пары примеров. Что ты заметил?
80 : 1 90 : 1 50 : 1 80:10 90:10 50:10
Сопоставляются случаи деления на 1 и на 10. Это позволяет повторить правило деления на 1 и обобщить правило деления на 10 (в ответе получаем число, которое показывает, сколько десятков содержится в делимом).
5. Можно ли, не решая уравнения, назвать значение неизвестного числа?
х*10=50 8*x=80 40:x = 4
Найти неизвестные в данных уравнениях учащиеся могут, используя новые знания.
Таким образом, изучение нового материала в процессе беседы и практической работы учащихся позволяет не только повторить ранее усвоенные знания, но и органически включить их в изучение нового, тем самым углубить их и как бы рассмотреть под другим углом зрения.
Использование приведенных выше заданий на уроке изучения нового материала вовсе не означает, что задание № 302 следует вообще исключить. Его выполнение имеет большое значение для составления таблицы умножения и деления. Это задание целесообразно разобрать устно в конце урока, обратив внимание на способ его выполнения. Но сама дидактическая задача этого задания при этом изменится. Следует обратить внимание на слова если и то, т. е. выяснить, почему, если мы имеем пример 2*10, то 10*2 = 20 и 20 : 2= 10, 20 : 10 = 2. Учащиеся сами ответят на этот вопрос либо учитель задаст им наводящие вопросы: какое свойство использовано при записи и решении второго примера? Какое правило использовано при составлении и решении третьего и четвертого примеров?
Расширение области чисел позволяет в III классе познакомить детей со случаями умножения и деления на 100, 1000, 10000.
Рассмотрим задание № 51 (1, 2), которое предлагает учебник для изучения нового вопроса:
1. Сравни числа в каждом столбике: во сколько раз увеличивается число, когда к его записи справа приписывается один нуль? два нуля? три нуля? 1 2 5 70 38
10 20 50 700 380
100 200 500 7000 3800
1000 2000 5000 70000 38000
2. Как изменяются числа 1000, 2000, 5000, 70000, если отбросить в их записи справа один нуль? два нуля? три нуля?
Если иметь в виду, что это первое задание, связанное с изучением нового вопроса, то прежде всего следует отметить, что, несмотря на то что в процессе работы над заданием учащиеся наблюдают, сравнивают, в основу формирования приема положены чисто внешние признаки. Следствием этого часто оказывается формальное усвоение данного вопроса: 10 с одним нулем, если к числу приписали один нуль, значит, увеличили его в 10 раз; 100 с двумя нулями, если к числу приписали два нуля, значит, увеличили его в 100 раз и т. д. (аналогично с делением).
Чтобы избежать формального подхода и повысить познавательный эффект при изучении данного вопроса, необходимо тщательно продумать, какие ранее усвоенные знания можно органически связать с изучением темы и подвести учащихся к осознанному и самостоятельному выводу.
Приведем возможный вариант.
Учащиеся самостоятельно выполняют задания:
1. Представь каждое из чисел в виде суммы его разрядных слагаемых 6666, 5555, 4444 (Числа записаны на доске, можно выполнить работу но вариантам.)
2. Запиши сумму — две тысячи плюс 200, плюс 20, плюс 2. Найди значение суммы.
3. Чем похожи и чем отличаются числа в каждом столбике? 236070 547007
236620 547000
236000 547020
Учащиеся обращают внимание на то, что во всех трех числах одинаково число тысяч, но есть числа, которые, кроме тысяч, содержат единицы других разрядов, и числа, которые содержат только единицы класса тысяч. Учитель обращает внимание учащихся на запись этих чисел.
Повторение разрядного состава многозначных чисел позволяет учащимся самостоятельно справиться со следующими заданиями:
4. Сравни данные выражения и числа: 2... 2*1
2*10... 2*100
2*1000... 2000
2*10000... 20000
5. Сколько раз можно повторить слагаемым число 1 000, чтобы получить 8000, 7000, 4000 и т. д.? Запиши ответ в виде произведения.
6. Сколько тысяч содержится в числах 4 000, 40 000, 400 000? Запиши эти числа в виде произведения, одним из множителей которого является число 1 000.
7. Даны числа: 8750, 9741, 9000, 5724, 51320. Выпишите числа, которые без остатка делятся на 10, 100, 1 000, и запиши с ними возможные примеры на деление на 10, 100, 1 000.
8. Назови числа, которые можно записать в виде произведения, где одним из множителей будут числа 10, 100, 1000: 8000, 82710, 2 700, 2 707, 45 730, 95 002, 375 000.
9. Составь из каждого примера на деление пример на умножение:
3800: 100 = 38 70000:1000 = 70 5400: 10 = 540
10. Задание № 51 из учебника математики целесообразно предложить учащимся после работы с вышеприведенными заданиями. В процессе выполнения этого задания рассмотренные случаи обобщаются.
Для того чтобы проверить, насколько сознательно учащиеся усвоили прием умножения и деления на 10, 100, 1 000, полезно предложить им задания, требующие применения знаний в несколько измененных условиях. Например:
1. Сравни выражения:
7000 + 700 + 70 + 7 и 7-1000 + 7-100 + 7-10 + 7;
8-1000 + 800 + 7-10 + 8 и 8000 + 8-100 + 70 + 4;
9-10000 + 8-1000 + 5-100 + 3-10 + 3 и 90000 + 8000 + 500 + 30 + 3
2. Реши уравнения:
х*1000 + 200 = 3 200
5*100 + x*4 = 540
8000 + х*100 + 50 = 8750
3. Записи возможные примеры на умножение и деление, используя следующие числа: 1, 10, 20, 100, 1000.
4. Составь возможные уравнения, используя следующие числа: 2, 10, 20, 100, х и реши их.
Учитель по своему усмотрению может использовать на уроке различные задания из вышеприведенных, но, подбирая последовательность заданий и продумывая вопросы к ним, он не должен
ограничиваться объяснением нового правила и запоминанием его в процессе упражнений. Чем больше будет установлено связей на уроке с уже изученными вопросами, тем сознательнее учащиеся усвоят новый материал и углубят ранее изученные вопросы... Кроме того, познавательная эффективность урока будет в этом случае значительно выше.
Тема “Умножение и деление чисел, оканчивающихся нулями” рассматривается на уроках во II классе в концентрах “Сотня” и “Тысяча”.
Учащиеся могут самостоятельно найти способ вычислений, если учитель предложит им следующие вопросы и задания:
1. 2*4 3*3 4*2 20*4 30*3 40*2
В чем сходство и различие данных пар примеров? Как можно рассуждать при вычислении второго произведения в каждой паре примеров?
2. Можно ли использовать те же рассуждения при нахождении частного?
40:2
90:3
100:5
80:4
3. Составь из каждого примера на деление два примера на умножение и реши их.
Число случаев умножения и деления чисел, оканчивающихся нулем, довольно ограничено в пределах сотни, поэтому совершенствование данного приема происходит в конце II класса в основном при изучении темы “Тысяча”.
Здесь тем более не следует показывать учащимся образец вычислений, так как они не только располагают достаточными знаниями для самостоятельного выполнения предложенных вычислений, но и в принципе уже знакомы с приемом умножения и деления чисел, оканчивающихся нулем.
Урок, посвященный изучению данного вопроса, целесообразно начать с задания:
— Сравни примеры каждой пары и реши их.
6*4 18:2 5*6 60*4 180:2 50*6
24:3 32 : 8 9:3 240 : 3 320 : 8 900 : 3
Затем учащимся предлагаются различные задания, в процессе выполнения которых данный вычислительный навык будет совершенствоваться в тесной связи с ранее изученными вопросами: увеличение и уменьшение числа в несколько раз; формирование представлений о переменной и постоянной величине; деление с остатком, например:
— Сравни примеры каждого столбика. В каком случае остаток будет больше? Почему?
320 : 4 540 : 9
321:4 544:9
323:4 542:9
Повторение табличных и внетабличных случаев деления.
Например, на какие числа можно разделить число 320, чтобы в частном получилось круглое число?
Умножение числа на 10. Разрядный состав двузначного числа. Например: вставь в окошки числа, чтобы получились верные равенства:
90:3 = П*3 840:4 = П*12 750:5=15*П 80:4 = П*2
Вычислительный прием умножения и деления чисел, оканчивающихся нулями, с которым учащиеся познакомились во II классе, совершенствуется затем в III классе, где устные вычисления заменяются письменными.
Сначала рассматривается случай умножения многозначного числа, оканчивающегося нулями, на однозначное число.
Приступая к изучению данного вопроса, не следует предлагать образец вычисления для случая 900-6, так как учащиеся могут вычислить данное произведение самостоятельно. Целесообразна начать урок с вопроса: “Как вы думаете, почему при умножении чисел, оканчивающихся нулями, следует делать такую запись?”:
6700 408000 X 6 X 9
(С алгоритмом письменного умножения на однозначное число учащиеся уже познакомились.)
Самостоятельный поиск ответа позволит учащимся сознательно выполнять впоследствии умножение и правильно оформлять запись. Опираясь на ранее полученные знания, учащиеся объясняют: 67 сот.*6 = 402 сот., поэтому в произведении приписываем два нуля; 408 тыс.*9=3672 тыс., поэтому в произведении приписываем три нуля.
Полезно также напомнить учащимся, что при умножении нуля на любое число получается нуль; возможно, что они укажут на это саки.
Умножение чисел, содержащих нули во втором множителе, а затем в первом и втором множителях, а также деление чисел, содержащих нули в делимом и делителе, являются как бы результатами обобщения тех знаний, которые учащиеся получили до рассмотрения указанных случаев. Кроме того, учащиеся знакомятся
со свойством умножения числа на произведение и деления числа на произведение.
Действительно, при вычислении результата в примерах
32*40 = 32* (4*10) = (32*4)*10
647*30=647* (3*10) = (647*3) * 10
имеют место случаи умножения на 10, 100... При рассмотрении случаев 8400*6000 = 84сот.* (6*10) = (84 сот.*6)*10 имеет место умножение на 10, 100, 1000, а также умножения чисел, оканчивающихся нулями, которые были рассмотрены ранее. Аналогично и при делении.
Опора на ранее изученные приемы позволяет учащимся сознательно применить при выполнении вычислений свойства умножения числа на произведение и деления числа на произведение.
Заметим, что характер приведенных заданий при изучении темы “Умножение и деление на 10, 100, 1 000”, а также темы “Умножение и деление чисел, оканчивающихся нулями” имеет в виду не только опору на ранее усвоенные знания, но и готовит учащихся к использованию свойств умножения числа на произведение и деления числа на произведение во II классе. Например:
Сравни данные выражения и числа:
2* 2*1
2*10 2*100
2*1000 200
— Назови числа, которые можно записать в виде произведения и в которых одним из множителей будут числа 10, 100, 1 000, 8000, 82710, 2700, 2707, 82730, 95002, 375000.
Таким образом, при подготовке к изучению на уроке нового материала необходимо стремиться к рассмотрению его в тесной взаимосвязи с другими вопросами курса, органически включать их в познание нового и видеть перспективу дальнейшего развития данного вопроса.
ПРОВЕРКА ДОМАШНИХ ЗАДАНИЙ НА УРОКЕ
Являясь одной из форм организации обучения в школе, домашняя работа имеет контролирующее, обучающее и воспитывающее значение. Работая дома, ученики не только закрепляют полученные на уроке знания, совершенствуют умения и навыки, но и приобретают навыки самостоятельной работы, воспитывают в себе организованность, трудолюбие, аккуратность, ответственность за порученное дело.
Эффективность домашней работы в процессе обучения во многом зависит от того, как учитель организует и направляет деятельность учащихся, связанную с выполнением домашних заданий. Руководство домашней работой он осуществляет не только в процессе задавания уроков на дом, но и в процессе их проверки. От способов и приемов проверки выполнения домашних заданий существенно зависит и характер их выполнения.
Дело в том, что при выполнении домашней работы учащиеся начальных классов нередко прибегают к помощи родителей. Зачастую задачи и примеры, выполненные ребенком на черновике, проверяются старшими, ошибки исправляются без какого-либо анализа, работа чисто и аккуратно переписывается в тетрадь.
Если учитель при проверке домашнего задания требует от учеников лишь воспроизвести то, что написано у них в тетрадях, или оценивает их работу при проверке тетрадей, то эта оценка часто не соответствует ни знаниям, ни затраченному труду ученика.
Такая проверка домашнего задания соответственно влияет и на характер его выполнения. Ученик старается только аккуратно оформить работу, не разобравшись до конца в тех заданиях, которые он должен был выполнить.
Следствием же такой методики проверки обычно является то, что ученик не может справиться с самостоятельной работой в классе даже в том случае, если она аналогична домашней, не умеет думать и рассуждать, не уверен в своих силах. Поэтому учителю не следует ограничиваться только проверкой домашней работы после уроков и простым воспроизведением выполненных учащимися домашних задании во время фронтальной проверки, а необходимо использовать различные способы и приемы, активизирующие деятельность учащихся и позволяющие установить, самостоятельно ли дети выполнили данную работу.
Продумывая способы проверки домашних заданий, учитель должен иметь в виду, что проверка выполняет не только контролирующую функцию, но и обучающую. Именно сочетание этих двух функции проверки позволяет повысить ее воспитательное значение и активизировать деятельность учащихся при проверке домашних заданий.
Проверка домашней работы должна стать органической частью урока, т. е. служить либо подготовкой к изучению нового материала, либо закреплению ранее изученных вопросов.
Рассмотрим такой пример. Дома учащиеся решали задачу: “В одной комнате 5 стульев, а в другой на 3 стула больше. Сколько стульев во второй комнате?” Цель урока, на котором проверяется выполнение этой домашней задачи, — формирование умения решать задачи на увеличение и уменьшение числа.
Продумывая последовательность заданий на данном уроке, учитель прежде всего имеет в виду проверку домашнего задания и, основываясь на этом этане, строит свою дальнейшую работу.
Задания выстраиваются в следующей последовательности:
1. Решите устно задачу: “В одной комнате 5 стульев, а в другой на 3 стула меньше. Сколько стульев в другой комнате?”
— Откройте тетради с решением домашней задачи. В чем сходство и различие классной и домашней задачи? (Сходство: даны числа 5 и 3. Вопросы задач одинаковые. Различие: в домашней задаче в условии дано, что во второй комнате стульев больше, а в условии классной задачи — меньше. Решение задач различно.)
— Каким действием решалась домашняя задача? Почему?
2. На доске текст: “На дереве сидели 5 птичек, 3 птички улетели”.
— Поставьте вопрос к данному условию. (Сколько птичек осталось?)
— Можно ли решить эту задачу так же, как домашнюю? (Нет. В домашней задаче 5 + 3 = 8, там есть слово “больше”, а здесь
птички улетели, их стало меньше.)
3. На доске текст: “На одном столе лежало 5 карандашей. Сколько карандашей лежало на другом столе?”
— Дополните условие задачи, чтобы она решалась так же, как домашняя,
Опять дети обращаются к домашней задаче. Сопоставляют ее решение с условием и по аналогии дополняют условие предложенной задачи.
Приведенные способы проверки активизируют деятельность учащихся. Контролируя, учитель обучает. При этом он использует различные методические приемы, способствующие формированию умения решать задачи, — это сравнение задач, дополнение условия задачи вопросом, недостающими данными. Предложенные задания постепенно усложняются: Дополнительные задания, связанные с проверкой домашнего задания, органически включаются в урок и служат достижению его цели.
Если проверку домашней задачи нельзя никак соотнести с целями урока, то при ее проверке полезно поставить ряд вопросов, которые позволят проверить, насколько учащиеся сознательно и самостоятельно подошли к решению задачи. Например, проверяя решение составной задачи: “У Коли было 15 коп. Он истратил на завтрак 10 коп., потом мама дала ему еще 20 коп. Сколько денег стало у Коли?”, можно поставить следующие вопросы:
1. Сколько денег у Коли осталось после того, как он позавтракал? (5 коп.)
2. На сколько копеек у Коли стало больше, чем было? (На 10 коп.) Почему? (Он истратил 10 коп., а мама дала ему еще 20 коп.)
3. Сколько раз Коля может еще позавтракать после того, как мама дала ему 20 коп.? (Еще 2 раза.)
4. Сколько копеек Коле не хватает, чтобы позавтракать третий раз? (5 коп., так как завтрак стоит 10 коп.)
Такая беседа позволит не только проверить самостоятельность решения домашней задачи, но и поможет ученику лучше разобраться в связях между числами, имеющими место в данной задаче.
Проверяя решение домашних примеров, можно повторить и закрепить различные вопросы курса. Это можно сделать, предложив учащимся следующие задания:
8—6 = 2 4 + 6=10 7—3 = 4 9—8=1 10—5 = 5 2 + 5 = 7 5 + 4 = 9 1+7 = 8
1. Прочитайте примеры, в которых вы находили сумму.
2. Прочитайте примеры, в которых находили разность.
3. Прочитайте примеры, при решении которых мы использовали переместительное свойство сложения.
4. Назовите случаи состава числа 10, которых нет в домашних примерах. Аналогичный вопрос можно задать по отношению к числам 7, 8, 9.
Способ проверки тех же примеров может носить косвенный или опосредствованный характер, например:
1) Составьте из всех примеров на вычитание примеры на сложение и прочитайте их.
Составляя пример на сложение,-ученик использует тот пример на вычитание, который он решил дома, т. е. по тому, как учащийся составит пример на сложение, учитель может судить о правильности решения домашнего примера. (Ответ: 3 + 4 = 7, 4 + 3 = 7.) Можно также уточнить, каким примером из домашнего задания пользовался ученик.
2) -Из каждого примера на сложение составьте два примера на
вычитание и прочитайте их.
Используя косвенный способ проверки, учитель может поставить перед учащимися и такие вопросы:
1) Какое число нужно вычесть из 8, чтобы получить 2? Какой пример из домашней работы помог вам ответить на этот вопрос? (8—6 = 2.)
2) Какое число надо увеличить на 4, чтобы получить 9? (5; пример: 5 + 4 = 9.)
3) Какое число надо уменьшить на 3, чтобы получить 4? (7;
пример: 7—3 = 4.)
Возможны задания и такого характера:
9—х=1. Укажите в домашней работе пример, который поможет вам найти неизвестное число в данном уравнении. (9—8=1.) Аналогичное задание предлагается с уравнениями:
х + 5 = 7 (2 + 5 = 7) х—5 = 5 (10—5 = 5)
В данном случае не имеет значения тот факт, что с решением уравнений на нахождение неизвестного уменьшаемого учащиеся еще не знакомы.
При проверке домашних примеров можно поставить перед учащимися обратную задачу, которую они могут решить, опираясь на выполненные дома примеры.
Например, на доске записаны равенства:
П + 7 = 8 С—3=4 8—П = 2 П+6=10 9— П = 1 П+4 = 9 10—П = 5 2 + П=7
Учитель предлагает задание: "Вставьте пропущенные числа, чтобы полученные равенства были верными”.
После этого примеры, записанные на доске, сопоставляются с примерами в тетради.
Все перечисленные способы могут быть использованы при проверке вычислений в любом концентре. Следует только учитывать
те новые знания и умения учащихся, которые они приобретают в процессе изучения курса.
Например, при проверке правильности вычислений возможна постановка таких заданий:
56—3 74—20 35 + 2 46 + 30 50—6 56 + 3 74 + 20 35 + 20 46—30 58—6
1) Прочитайте примеры, в которых находится сумма двузначных чисел.
2) Прочитайте примеры, в которых находится разность двузначных чисел.
3) Прочитайте примеры, при решении которых вы использовали вычитание из числа 10.
4) Прочитайте примеры, в которых ответ равен: 3 десяткам, 7 единицам; 5 десяткам 5 единицам; 1 десятку 6 единицам.
5) Прочитайте примеры, в которых данное число ув'„ личпвает-ся на несколько единиц, на несколько десятков; уменьшается на несколько единиц, на несколько десятков.
При проверке решения тех же примеров можно использовать и такой прием. На доске запись:
56—3 . . . 56 + 3
74—20 . . . 74+-20
35 + 2 . . . 354-20
46 + 30 . . . 46—30
50—6 . . . 58—6
Ученикам предлагается сравнить данные выражения, воспользовавшись для этой цели примерами, которые решались дома. (Ответ: 56—3<56 + 3, так как 56—3 = 53, 56 + 3 = 59, 53<59.) Можно усложнить задание, сравнивая числовые выражения не в той последовательности, в какой они даны в домашнем задании, например: 74—20 . . . 58—6; 35 + 20 . . . 74—20. Это потребует от учеников еще большего внимания при проверке.
Использование различных способов проверки для закрепления и повторения возможно и при проверке решения уравнений. Например, учащиеся решали дома уравнения: x+4 = 7, 3+x=6, х + 7= 10. Учитель может предложить такие задания:
1) х, 7, 6, 3. Составьте из данных чисел одно из уравнений, которое вы решали дома. (3 + x = 6.)
2) Можно ли составить другие уравнения с этими же числами? (x + 6 = 7; x + 3 = 6; x + 3=7.) Решите уравнения.
Пока учащиеся решают самостоятельно составленные уравнения в тетрадях, учитель проходит по классу и выясняет, как ученики справились с домашним заданием. Слово предоставляется ученику, который допустил в домашней работе ошибку.
3) Почему в уравнении х + 4 = 7 x = 3? (Если подставить вместо х число 3, то получим верное равенство 3 + 4 = 7.)
4) Какое из чисел —2, 5, 3, 4, 8 —является ранением уравнения x+7= 10? Почему?
Особую значимость приобретает проверка домашней работы, если она органически связана с изучением нового материала. Учителю в этом случае необходимо продумать как само домашнее задание, так и вопросы, связанные с его проверкой. Рассмотрим, как можно организовать работу на примере изучения темы.
В начале урока проверяется домашняя задача: “Для школы купили 10 портретов по 3 руб. и 2 портрета по 5 руб. Сколько денег уплатили?”
Учитель заранее пишет краткую запись домашней задачи на доске:
10 п. по 3 р. 2 п. по 5 р. Помимо этого на доске записана краткая запись другой задачи:
1 — 10 п. по 3 р.
II —10 п. по 5 р.
— Посмотрите, на доске записаны две задачи, одну из них вы решали дома. (По краткой записи воспроизводится домашняя задача и ее решение.)
— А теперь послушайте вторую задачу: “Одна школа купила 10 портретов по 3 руб., а другая 10 портретов по 5 руб. Сколько денег уплатили за все портреты?”
Выясняется сходство и различие классной и домашней задач,
предлагается записать решение классной задачи выражением 3*10 + 5*10.
— Можно решить классную задачу другим способом? (Если учащиеся затрудняются, учитель ставит вопрос по-другому: “Можно ли решить классную задачу таким способом: (3 + 5)*10?”)
— Можно ли решить домашнюю задачу другим способом? (Нет.) Почему? (Количество купленных портретов различно.)
Сопоставление классной и домашней задач помогает учащимся понять, в каком случае мы можем сумму двух произведений заменить умножением суммы на число.
— Как можно изменить условие домашней задачи, чтобы можно было решить ее двумя способами?
Изменения вносятся в краткую запись домашней задачи на доске:
2 п. по 3 р. 2 п. по 5 р.
— Запишите решение этой задачи выражением: 3*2 + 5*2=(3 + 5)*2 =
Таким образом проверка домашнего задания подвела учащихся к изучению нового материала.
После проведения такой работы можно предложить ученикам решение примеров двумя способами (№ 491, 1-й и 2-й столбики),
(2+8)*8= (3 + 4)*6 = 2*8 + 8*8= 3*6 + 4*6=
На дом предложить № 491 (3-й и 4-й столбики):
(10 + 9)*4 (9+1)*7 (10+2)*8 (6 + 4)*10
Проверку этого домашнего задания на уроке можно провести следующим образом:
1. Найдите произведения, используя домашние примеры:
19*4 10*7 12*8 10*10
Почему можно воспользоваться домашними примерами?
2. Сравните выражения:
(10 + 9)*4 ..... 19*4 (9+1)*7 ..... 10*7
3. Вставьте пропущенные числа, чтобы равенства были верными. Используйте домашние примеры.
(10+¨ )*4=10*4+¨ *4
(10 + 2)* ¨ = 10*8 + 2*8 и т. д.
В данном случае в ходе проверки закрепляются знания, полученные на предыдущем уроке. На дом задается № 500:
7*2 + 7*8 10*2+10*3 4*6 + 6*6 2*10 + 3*10
Проверка осуществляется следующим образом:
— Вычислите выражения, используя домашние примеры:
7*(2 + 8)
6*(4 + 6)
10*(2 + 3)
Какие примеры из домашней работы вы использовали? Обоснуйте свой ответ.
В учебниках не предусматривается взаимосвязь домашнего задания с материалом, предлагаемым для каждого следующего урока, поэтому учителю следует самому творчески подходить к выбору заданий для домашней работы. Переходя к изучению темы “Умножение суммы на число”, целесообразно предложить, например, такие задания на дом:
1. Найдите значения выражений: 3*2 + 4*2, 5*3 + 4*3, 3*5 + 4*5, 3*4 + 6*4.
2. Задача: “3 девочки сделали для елки по 4 красных хлопушки, а 3 мальчика — по 5 синих хлопушек. Сколько всего хлопушек
сделано для елки?” Запишите решение задачи выражением. Сделайте к задаче рисунок, обозначая красные хлопушки -красными кружками, а синие — синими.
Проверку домашнего задания следует органически включить в урок, связанный с изучением нового материала.
Рассмотрим возможный вариант такого урока.
В устный счет целесообразно включить упражнения, связанные с повторением табличных случаев умножения. Затем предложить найти значения выражений, записанных на доске: (3 + 4)*2, (5+4)*3, (3 + 4)*5, (3 + 6)*4. Работа проводится устно, на доске записываются ответы. Затем учитель предлагает открыть тетради с домашним заданием и сравнить решенные примеры с домашними. Выясняется, не обратили ли учащиеся внимание на то, чем похожи между собой примеры, решаемые дома. (В каждом выражении одинаковые вторые множители.)
— Запишите в тетради выражение (учитель диктует): “Сумму чисел 3 и 4 умножить на 2”. Запишите, чему равно значение выражения. Выпишите пример из домашнего задания, в котором получился такой же ответ. Запись в тетради:
(3 + 4)*2=14 3*2 + 4*2 = 14
Аналогичная работа проводится со следующими выражениями (учитель диктует, учащиеся записывают в тетради):
(5 + 4)*2= 18 (3 + 4)*5 = 35 (3 + 5)*4 = 36 5*2 + 4*2=18 3*5 + 4*5 = 35 3*4 + 6*4 = 36
— Посмотрите внимательно на записанные пары примеров. Чем похожи между собой первые примеры каждой пары? (Везде сумма умножается на число.) Сравните между собой вторые примеры каждой пары и ответьте на вопрос: как можно умножить сумму на число?
После этого рассматривается рисунок 3 к домашней задаче. Обсуждается, нельзя ли задачу решить другим способом.
Если учитель систематически связывает проверку домашнего задания с изучением нового материала, с проведением устного счета, с закреплением и повторением материала, то учащиеся более ответственно относятся к домашнему заданию, стараются выполнить его самостоятельно, чтобы быть готовыми к тем вопросам, которые ждут их на уроке.
Полезной в этом же плане является работа и по составлению различных вопросов к домашнему заданию самими учащимися. Данная работа является естественным продолжением использования различных приемов проверки домашнего задания учителем и служит не только активизации деятельности учащихся во время проверки, но и формированию у них навыков самоконтроля. Начать эту работу учитель может следующим образом. На одном из уроков он сообщает учащимся, что сегодня проверять домашнюю работу будет кто-то из учащихся (такую работу можно начать в конце обучения во II классе). Приведем конкретный пример.
Домашняя работа: № 936, 938. Задача: “В одну школу привезли 298 парт, а в другую на 123 парты больше. Сколько парт привезли в обе школы?”
№ 938. 340+17*3 + 200 3*26—44:22
860—24*2+120 500—100:25*1-10
750 + 48:2—200 800—56:4*4-40
При проверке домашней задачи ученик поставил вопросы:
— Во сколько действий решили задачу? Какое первое действие? Почему? Какое второе действие? Почему? Измените условие задачи, чтобы в первом действии было вычитание.
Учитель дополнил вопросы ученика: “Как по-другому можно сформулировать условие задачи, чтобы ее решение было таким же?” При проверке примеров (1-й столбик) ученик поставил вопросы:
— Прочтите пример, в котором самый большой ответ. Прочтите пример, в котором самый маленький ответ. Расскажите, как решали первый пример. Почему сначала нашли произведение 17*3?
Учитель дополнил. “Назови ответы примеров в порядке возрастания”. Такие же вопросы можно предложить при проверке 2-го столбика.
Безусловно, систематическая работа учителя по использованию различных приемов проверки домашних заданий не прошла бесследно. У учащихся постепенно формировалась способность самостоятельно анализировать то, что они выполняли дома.
Можно даже предлагать учащимся дома продумать, как они будут проверять домашнее задание в классе, какие вопросы и задания предложат. Постановка вопросов самими учащимися является полезной в различных аспектах, поэтому не следует учителю жалеть времени на проведение такой работы.
Взаимопроверка домашнего задания — это наиболее высокая ступень самостоятельной деятельности учащихся. К использованию этого приема учитель может приступить только после того, как в процессе своей работы будет применять на уроке различные приемы проверки домашней работы. Только в этом случае взаимопроверка будет носить не формальный характер, а осуществляться сознательно и ответственно.
ПОДБОР ЗАДАНИЙ ДЛЯ ИНДИВИДУАЛЬНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Проведение самостоятельной работы на уроках математики прочно вошло в практику начальной школы.
Самостоятельная работа проводится без непосредственной помощи учителя в процессе ее выполнения, но это вовсе не исключает, а, наоборот, предполагает руководящую роль учителя, так как проведение самостоятельной работы — это фактически решение той или иной дидактической задачи, которую ставит учитель на уроке. Это подготовка детей к изучению нового материала усвоение новых знаний, расширение и углубление их, формирование вычислительных навыков и другие задачи.
Учитель также может поставить перед собой задачу проверить знания, умения и навыки учащихся. В этом случае дается проверочная самостоятельная работа.
В процессе самостоятельной работы встречаются различные виды деятельности учащихся (самостоятельная деятельность по образцу, предложенному учителем, применение знаний в аналогичных условиях, творческая деятельность).
Организуя самостоятельную работу, учитель обычно предлагает всему классу общее задание или дифференцирует задания пс вариантам (два или четыре). Задания в каждом из вариантов чаще всего аналогичны по содержанию и требуют от учащихся использования однородных способов выполнения работы (независимо от дидактической задачи и видов деятельности учащихся), например:
— Решите самостоятельно уравнения:
Вариант I Вариант II
7—x = 5 8 + х=10
4 + х = 8 9—х=4
Время выполнения такой работы каждым учеником в классе, естественно, различно. Поэтому учащимся, которые быстро справились с заданием, учитель предлагает индивидуальную работу. В одном случае это просто увеличение объема работы, т. е. предлагается решить еще одно такое же уравнение, в другом случае ^то задание, требующее других способов решения, или задание на сообразительность. И в том и в другом случае ученик получает индивидуальное задание и выполняет его самостоятельно.
Итак, индивидуальная самостоятельная работа должна учитывать индивидуальные особенности ученика: темп его работы, способность к предмету. Обычно такие работы выполняют в классе сильные ученики. Иногда учитель сразу предлагает таким ученикам карточки с содержанием индивидуальной самостоятельной работы. Можно наблюдать и другую противоположность. Учитывая индивидуальные особенности, учитель предлагает карточки с заданием слабым ученикам или ученикам, у которых, по его мнению, есть пробелы в знаниях, а всему классу дает общее задание.
Из всего сказанного можно сделать вывод, что индивидуальные самостоятельные работы обычно выполняют одни и те же ученики (либо сильные, либо слабые), ученики же, темп работы которых совпадает с планируемым учителем, ограничены выполнением только самостоятельной работы. Возникает вопрос: можно ли сделать так, чтобы предложенная самостоятельная работа могла бы по сути своей стать индивидуальной для каждого ученика?
Творчески работающие учителя не ограничиваются в процессе обучения включением только самостоятельных работ. Осуществляя индивидуальный подход к учащимся, изучая и зная их способности и наклонности, они планируют на некоторых уроках проведение индивидуальных самостоятельных работ, подбирая для каждого ученика задания в соответствии с их возможностями. Если такая работа проводится систематически, то в процессе ее выполнения уровень самостоятельности ученика повышается, он может выполнять уже более сложные задания без помощи учителя. Но и в этом случае индивидуальная самостоятельная работа нацелена в основном на усвоение знаний, умений и навыков.
Возникает вопрос: можно ли индивидуальную самостоятельную работу использовать не только с целью усвоения знаний, умений и навыков, но и рассматривать ее как средство развития творческой активности учащихся, инициативы, развития их познавательной самостоятельности?
Одним из средств выполнения этой задачи является использование в самостоятельной работе заданий, одинаковых по содержанию, но различных по способу выполнения. В отличие от обычных заданий, в которых одинаково содержание и одинаков способ выполнения (назовем их условно задания I вида), использование заданий, одинаковых по содержанию, но различных по способу выполнения (задания II вида), дает возможность каждому ученику проявить свою индивидуальность и свои возможности.
Задание, в котором предлагалось решить самостоятельно уравнения: 7—х=5, 4 + х = 8, можно отнести к I виду.
Половина учащихся класса получила задание, одинаковое по содержанию и по способу его выполнения. Если несколько изменить инструкцию, можно преобразовать данное задание в задание II вида. 'Оно будет выглядеть так: “Составьте различные уравнения р числами 7, 5, 4, х, 8 и решите их”. Получив для самостоятельной работы такое задание, каждый ученик индивидуально подходит к его выполнению. Учащиеся составляют, например, уравнения: 4 + x = 5, 7—х = 5, 7 + х = 8, 5+x = 8, 5—х = 4, 8—х = 7 и т. д.
Одни ученики смогут записать только одно-два уравнения и решить их, другие запишут большее число вариантов. Деятельность учащихся носит поисковый, творческий характер, так как для выполнения задания необходимо не только умение решать уравнения, но и понимать взаимосвязь между компонентами и результатом действий, т. е. использовать определенные знания для решения предложенной задачи. Учащиеся должны понимать, что
случай 5 + x = 4 не имеет решения, и уметь объяснить почему, ориентируясь на саму запись уравнения.
В самом содержании задания заложен уже индивидуальный подход к учащимся, и учителю не нужно будет дополнительно предлагать детям карточки с индивидуальными заданиями.
Используя те же числа, учитель может предложить и другое задание, которое также будет характеризоваться одинаковым содержанием, но различными способами выполнения, например: “Используя данные числа, составьте уравнения, в которых неизвестное равно нулю”. (x+5=5, x + 4 = 4, 4—х = 4 и т. д.) При анализе задания учитель может подвести детей к обобщению, предложив им сравнить все записанные уравнения и указать на их особенность, хотя не исключена возможность, что некоторые ученики сами обратят внимание на это уже в процессе выполнения работы.
Рассмотрим в качестве примера задание геометрического содержания (оно взято из книги: Пышкало А. М. Методика обучения элементам геометрии в начальных классах. М., 1973): “Разделите четырехугольник отрезком на части так: 1) чтобы обе части были треугольниками; 2) чтобы обе части были четырехугольниками; 3) чтобы одна часть была треугольником, а другая четырехугольником; 4) чтобы одна часть была треугольником, а другая — пятиугольником”. Приведенное задание позволяет учителю организовать самостоятельную работу в классе, используя четыре варианта. Процесс выполнения задания, безусловно, требует от учащихся поиска.
Преобразуем данное задание, т. е. изменим его инструкцию так, чтобы она отвечала особенностям заданий II вида: “Разделите четырехугольник отрезком на части так, чтобы получилось две геометрические фигуры. Какие это фигуры?”
Задание в таком виде даст возможность каждому из учеников проявить свою индивидуальность, самостоятельность и творческую активность. Кроме того, сам процесс организации самостоятельной работы упростится, так как учитель предложит единое задание всему классу. В силу индивидуальных особенностей одни ученики могут ограничиться одним способом, другие — двумя, а третьи рассмотрят все возможные случаи.
Систематическая работа по выполнению заданий II вида оказывает существенное влияние на развитие творческого подхода к ним, способствует проявлению индивидуальных особенностей ученика и тем самым формирует самостоятельность как черту личности, помогает каждому ученику поверить в свои возможности и совершенствовать их в процессе обучения. Эти задания, естественно, следует усложнять от класса к классу, но начинать нужно, безусловно, с самых простых. Лучше, если эти задания на началь-
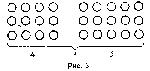
ном этапе будут носить практический характер. Например, в I классе при изучении задач на сравнение чисел учитель может предложить следующие задания: “Разложите 8 треугольников (у каждого ученика на парте набор треугольников) в два ряда так, чтобы в верхнем ряду треугольников было больше, чем в нижнем (рис. 4). На сколько треугольников в верхнем ряду больше, чем в нижнем?” Особенность такого задания опять же состоит в том, что его содержание одинаково для всех учеников класса, но способ его выполнения индивидуален.
Каждый ученик должен обосновать свой вариант. При этом одни могут предложить сразу три способа, другие — два, а третьи — один. Каждый выполнит задание в силу своих индивидуальных возможностей.
— Нарисуйте 7 кружков, а в нижнем ряду нарисуйте столько кружков, чтобы их было меньше, чем в верхнем. На сколько в верхнем ряду кружков больше, чем в нижнем? (Задание имеет шесть вариантов ответов.)
Ко II виду можно отнести также задания, которые есть в учебнике и связаны с записью неравенств и со сравнением математических выражений. Способ их выполнения не представляет собой трудности для учеников, поэтому их также можно использовать на более раннем этапе проведения индивидуальных самостоятельных работ. Вот эти задания:
1) П<5. Вставьте в окошко число так, чтобы полученное неравенство было верным. Запишите это неравенство.
2) 2+П<4 + 5. Вставьте в окошко число так, чтобы получились верные неравенства. Запишите эти неравенства и обоснуйте свой ответ.
2+К4 + 5, обоснование: 3<9;
2 + 4<4 + 5, обоснование: 6<9;
2 + 5<4 + 5, обоснование: 7<9, и т. д.
3) 5+П>5+П. Вставьте в окошки числа так, чтобы получились верные неравенства. Запишите их и обоснуйте свои ответ. (5 + 2>5+1, обоснование: 7>6; 5 + 4>5 + 2, обоснование: 9>7.)
Совершенствуя вычислительные навыки на более позднем этапе, учитель может при проведении индивидуальной самостоятельной работы использовать задания:
1. Запишите примеры на сложение, в которых сумма равна 12.
2. Запишите примеры на вычитание, в которых разность равна 9.
3. Запишите примеры на вычитание с уменьшаемым, равным
21. Вычислите разность.
4. Запишите примеры на вычитание, в которых вычитаемое равно 15. Вычислите разность.
5. Запишите примеры на сложение, в которых второе слагаемое равно 8. Вычислите сумму.
6. Запишите примеры на сложение, в которых сумма равна 20.
7. Используя числа 10, 8, 2, 4, 6, составьте различные примеры на вычитание (возможны семь способов записи примеров).
Предлагая для самостоятельной работы всему классу задания такого содержания, учитель обеспечивает индивидуальный подход к его выполнению у каждого ученика, так как одна группа учеников за отведенное время сможет записать и вычислить семь-восемь примеров, другая четыре-пять, а третья два-три. В процессе проверки учащиеся могут контролировать друг друга, узнавать новые способы выполнения задания, обсуждать их.
При усвоении нумерации чисел и их последовательности в натуральном ряду для индивидуальной самостоятельной работы возможно использование таких заданий:
1) 2 ... Какую цифру можно записать вместо точек, чтобы получить числа, меньшие, чем 29? Запишите возможные случаи и обоснуйте свой ответ. (21<29, 22<29, 23<29 . . . )
2)3 ... >3 .... Какие цифры можно записать вместо точек, чтобы получить верные неравенства? Запишите возможные неравенства. (32>31, 33>30, 35>31 . . . )
Задания, одинаковые по содержанию, но различные по способу выполнения, целесообразно использовать также для индивидуальных самостоятельных работ при совершенствовании навыков умножения и деления.
Примеры заданий:
1. Запишите примеры на умножение, в которых произведение равно 24. (6*4 = 24, 3*8 = 24, 12*2 = 24, 24*1=24.)
2. Запишите примеры на деление, в которых частное равно 2. (4:2 = 2, 6:3 = 2, 8:4 = 2 и т. д.)
3. Запишите примеры на умножение, в которых первый множитель равен 8, и решите их.
4. Запишите примеры на деление, в которых делимое равно 72, и решите их.
5. Запишите примеры на деление, в которых делитель равен 5, и решите их.
Эти задания не только предоставляют возможность осуществить индивидуальный подход к их выполнению, но и способствуют усвоению терминологии — названий, компонентов и результатов действий.
— Используя только эти числа: 12, 3, 2, 6, 4, запишите примеры на деление. (12:2=6, 6:2 = 3, 12:3 = 4, 6:3 = 2, 12:4 = 3, 12:6 = 2, 4:2=2.)
При изучении геометрического материала также возможно использование заданий, одинаковых по содержанию, но различных по способам выполнения.
Приведем приметы.
1. Вырежьте из клетчатой бумаги прямоугольники одинаковой площади.
Если эти задания предлагаются впервые, они представляют для ученика проблемную задачу. Он сам задает нужную площадь, а затем ищет способ, как получить (вырезать) прямоугольники за-
данной площади. Он может воспользоваться знанием формулы площади прямоугольника и клетчатой бумагой, из. которой ему предложено вырезать фигуры. Ученик может пойти и другим путем. Сначала он вырежет прямоугольник, задав его длину и ширину (например, длина 6 см, ширина 4 см, площадь 24 кв. см), а затем будет искать возможности получения этой площади. Здесь индивидуальность проявится в различных аспектах: и в подходе к решению задачи, и в выборе конкретных данных.
2. Вырежьте из клетчатой бумаги прямоугольники одинакового периметра. (Методика выполнения задания аналогична предыдущему заданию.)
После выполнения практических заданий учитель может предложить задания на построение.
3. Постройте прямоугольники, площадь которых равна 12 кв. см. Обоснуйте свой ответ. Вычислите периметр прямоугольников.
Ответ: длина 12 см, ширина 1 см, 12*1 = 12 (кв. см). (12+1)*2 = 26 (см); длина 6 см; ширина 2 см; 6*2=12 (кв. см); (6 + 2)*2=16 (см); длина 4 см; ширина 3 см; 4*3=12 (кв. см); (4 + 3)*2= 14 (см).
4. Постройте прямоугольники, периметр которых равен 20 см. Обоснуйте свой ответ. Вычислите площадь.
Ответ: длина 9 см, ширина 1 см, (1+9)*2 = 20 (см). 1*9 (кв. см); длина 8 см; ширина 2 см; (8+2)*2 = 20 (см); 8*2 = = 16 (кв. см); длина 7 см; ширина 3 см; (7 + 3)*2 = 20 (см); 7*3 = 21 (кв. см); длина 6 см; ширина 4 см; (6 + 4)*2 = 20 (см); 6*4 = 24 (кв. см); длина 5 см; ширина 5 см; (5 + 5)*2 = 20 (см); 5*5 = 25 (кв. см).
Анализ всех возможных способов выполнения задания имеет определенное познавательное значение. При его выполнении целесообразно, например, выяснить, какие стороны должен иметь прямоугольник с периметром в 20 см, чтобы его площадь была наибольшей. Ответ на данный вопрос способствует осознанию того факта, что квадрат следует рассматривать как частный случай прямоугольника.
Мы рассмотрели на примере различных вопросов курса возможность составления заданий, одинаковых по содержанию, но различных по способу выполнения. Задания II вида, так же как и задания I вида, помогают совершенствованию вычислительных навыков и усвоению знаний. Использование заданий II вида можно рассматривать как один из методических приемов индивидуального подхода к учащимся в процессе обучения, который способствует продвижению в развитии каждого ученика.
