Диагонали параллелепипеда
|
• |
Диагонали |
B1 |
C1 |
параллелепипеда |
|
||
A1 |
D1 |
пересекаются в |
|
|
одной точке и |
|
|
делятся этой |
O |
|
точкой пополам |
B C
A D
AO OC1 AO1 OC BO OD1 B1O OD
Диагональные сечения призмы
•Сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани, называются
диагональными
сечениями
•Диагональные сечения призмы являются
параллелограммами
|
E1 |
D |
|
|
|
A1 |
|
C |
|
B1 |
|
E |
D |
|
A |
C |
|
B |
|
E1 |
D |
|
|
|
A1 |
|
C |
|
B1 |
|
E |
D |
|
A |
A |
|
C |
||
|
B |
|
E1 |
D |
|
|
|
A1 |
|
C |
|
B1 |
|
E |
D |
|
A |
C |
|
B |
|
E1 |
D |
|
|
|
A1 |
|
C |
|
B1 |
|
E |
D |
|
C |
B |
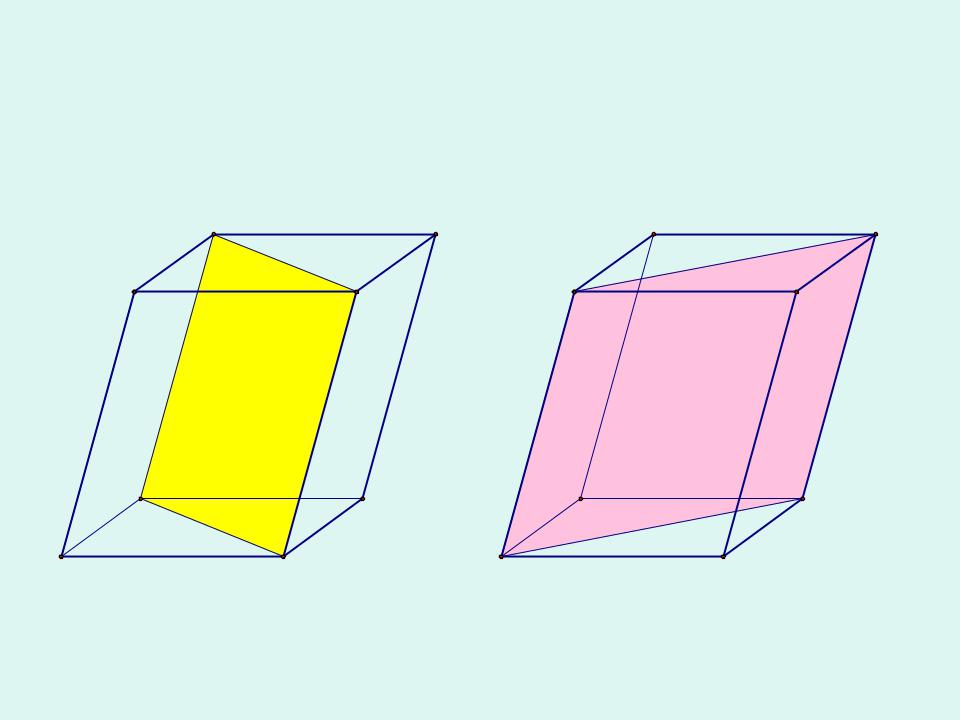
Диагональные сечения параллелепипеда
B |
C1 |
B |
C1 |
1 |
|
1 |
|
A |
D1 |
A |
D1 |
1 |
|
1 |
|
B |
A |
C
D A
B C
D
Площадь поверхности призмы
•Площадью полной поверхности
призмы называется сумма площадей всех её граней Sполн
•Площадью боковой поверхности
призмы называется сумма площадей её боковых граней Sбок
Sполн Sбок 2Sосн
Теорема о площади боковой поверхности прямой призмы
Теорема.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы
Sбок Pосн H
Доказательство теоремы
•Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте H призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т.е. равна сумме произведений сторон основания на высоту H. Вынося множитель H за скобки, получим в скобках сумму сторон основания, т.е. периметр P.
F1 |
A1
F
A 
E1 |
D1 |
B1 |
C1 |
E |
D |
BC
Sбок SABB1A1 SBCC1B1 SACC1A1
AB AA1 BC BB1 AC CC1
AB H BC H AC H
AB BC AC H
A1
PVABC H
A 
C1
B1 |
C
B |