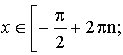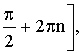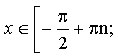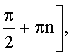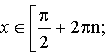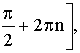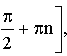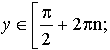Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Криворожский экономический институт КНЕУ им. В. Гетьмана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

алгебра1.doc

Скачиваний:

Добавлен:

15.07.2019

Размер:

2.47 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 33

Побудова графіків тригонометричних функцій

Графік кожної з тригонометричних функцій досить побудувати на проміжку, що дорівнює найменшому додатному періоду, а потім його можна продовжити на всю область визначення. При побудові графіків за точками скористаємось геометричним тлумаченням кожної з тригонометричних функцій на одиничному колі.

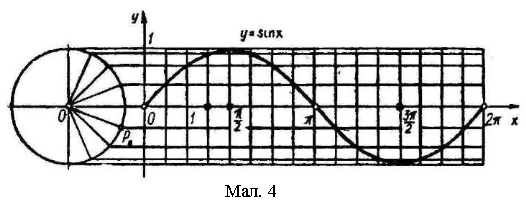
Графік функції y=sinx побудуємо на відрізку [0;2π]. Оскільки синус числа α – це ордината точки одиничного кола, в яку переходить точка Р₀ (1;0) при повороті навколо центра на α рад, то побудуємо систему координат. Позначимо на осі Ох відрізок [0;2π], довжина якого наближено дорівнює 2π≈6,28. Розіб’ємо відрізок [0;2π] і коло, починаючи від точки Р₀, на 16 рівних частин. Через кожну точку поділу кола проведемо прямі, паралельні осі Ох. З кожної точки Р_α поділу кола проведемо перпендикуляри до осі Ох, довжини яких дорівнюють ординаті, а значить синусу кута, утвореного радіусом ОР_α з віссю Ох і виміряного у радіанах. Кожна з цих ординат відповідає абсцисам α, позначеним точками поділу відрізка [0;2π] на осі Ох. Провівши прямі, паралельні осі Оу у кожній точці поділу цього відрізка, до перетину з відповідною паралельною прямою, дістанемо у перетині точки графіка функції y=sinx. Проведена через ці точки суцільна крива називається синусоїдою.

Оскільки функція y=sinx періодична з періодом 2nπ, де тобто y=sin(x+2nπ), то для продовження графіка за межі відрізка [0;2π] досить виконати побудову графіків функцій виду

y=sin(x+2π), y=sin(x–2π), y=sin(x+4π), y=sin(x–4π), y=sin(x+6π),

y=sin(x–6π), … ,

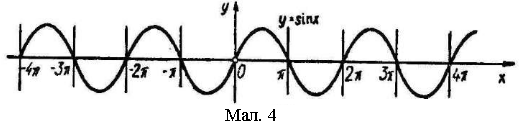
паралельно переносячи графік функції y=sinx на 2π, 4π, 6π, … одиниць вліво і вправо (мал.4).

Властивості тригонометричних функцій

Функція Влас- тивість	y=sinx	y=cosx	y=tgx	y=ctgx
1. Область визначення	xR	xR	xR, x nZ	xR, xn, nZ
2. Множина значень	y[-1;1]	y[-1;1]	y R	y R
3. Парність (непарність)	Непарна	Парна	Непарна	Непарна
4. Періоди-ність	Т=2n, nZ	Т=2n, nZ	Т=n, nZ	Т=n, nZ
5. Набуває нульових значень	x =n, nZ	x = nZ	x =n, nZ	x = nZ
6. Проміжки зростання	nZ	x[-+2n; 2n], nZ	nZ	Не має
7. Проміжки спадання	nZ	x[2n; +2n], nZ	Не має	x[n; +n], nZ
8. Набуває додатних значень	у[2n; +2n], nZ	nZ	nZ	nZ

Функція Влас- тивість	y=sinx	y=cosx	y=tgx	y=ctgx
9. Набуває від’ємних значень	у[+2n; 2+2n], nZ	nZ	nZ	nZ
10. Найбільше значення	у=1 при x = nZ	у=1 при x =2n, nZ	Не має	Не має
11. Найменше значення	у=-1 при x = nZ	у=-1 при x =+2n, nZ	Не має	Не має

Домашнє завдання.

Р.І; §5-7, с.83 №25, 30 (б), 39 (1, 8, 9, 10).

Лекція № 51

Тема: Найпростіші тригонометричні рівняння.

План:

Взаємообернені функції, їх властивості.
Обернені тригонометричні функції.
Розв’язування найпростіших тригонометричних рівнянь:

- sinx=a, |a|≤1;

- cosx=a, |a|≤1;

- tgx=a, ctgx=a.

Поняття про обернену функцію. Під час розв’язування різних задач часто доводиться обчислювати значення функції за даним значенням аргументу. Наприклад, обчислювати площу S квадрата за довжиною його сторони за формулою S=a², яка задає залежність (функцію) площі від довжини a сторони квадрата. Проте часто доводиться розв’язувати обернену задачу: якою має бути сторона квадрата a, щоб площа S мала наперед задане значення або обчислити час t, який витрачено тілом при рівномірному русі, якщо воно пройшло шлях певної довжини. Якщо (де  - стала) – формула шляху, яка задає лінійну функцію, то - функція аргументу t. Якщо визначити t з формули шляху, то дістанемо іншу функцію також лінійну, але відносно аргументу s, яку в загальному вигляді позначимо Функцію називають оберненою до функції S=a², а - оберненою до

Функція f, яка має обернену, називається оборотною.

Необхідною і достатньою умовою існування оборотної функції є така: вона має набувати кожного свого значення лише для одного значення аргументу.

Оберненою до даної оборотної функції у = f (х) називається така функція х = φ (у), яка кожному у із множини значень функції у = f (х) ставить у відповідність єдине число х із її області визначення.

Якщо поміняти позначення незалежної і залежної змінних, то обернену функцію до у = f (х) запишемо у вигляді у = φ (х).

Розглянемо алгоритм знаходження формули функції, оберненої до даної.

1) З’ясовуємо, чи є функція у = f (х) оборотною на всій області визначення. Якщо ні, то виділяємо підмножину області визначення, де існує функція, обернена до у = f (х).

2) Розв’язуємо рівняння у = f (х) відносно змінної х, тобто знаходимо функцію х = φ (у), яка є оберненою до у = f (х).

3) Міняємо позначення змінних: незалежну змінну позначаємо х, а залежну – у. Дістаємо функцію у = φ (х), обернену до у = f (х) у прийнятих позначеннях змінних.

Можна довести загальне твердження: графік функції φ, оберненої до функції f симетричний графіку f відносно прямої у = х.

Сформулюємо без доведення таку властивість оберненої функції: якщо функція f зростаюча (спадна) на проміжку І, то вона оборотна. Обернена до f функція φ, визначена в області значень f, також в зростаючою (спадною).

Тригонометричними рівняннями називаються рівняння, у яких невідома (змінна) входить лише під знак тригонометричної функції.

Домашнє завдання.

Р.ІІ; §1,2, с.125 запитання №1-11; розв’яз. №11 (1-10); с.126 №1 (1-10).

Лекція №55

Тема: Тригонометричні нерівності.

План:

Алгоритм розв’язання тригонометричних нерівностей sinx>a; sinx<a
Алгоритм розв’язання нерівностей соsx<a; cosx>a
Алгоритм розв’язання тригонометричних нерівностей tgx>a; tgx<a
Алгоритм розв’язання тригонометричних нерівностей ctgx>a; ctgx<a

sinx<a; |a|≤1

В системі координат намалювати одиничне коло.
На лінії значень синуса (вісі Оу) поставити значення а (|a|≤1).
Через отриману точку провести пряму перпендикулярну до Оу.
Пряма розбила одиничне коло на дві частини: верхню і нижню (зверху значення більші за а, знизу – менші).
Вибираємо нижню частину до значення – 1, якій відповідає нижня дуга.
Позначаємо відповідний центральний кут та визначаємо координати кінців дуги (позначивши напрям орієнтації – за годинниковою чи проти годинникової стрілки).
Записуємо відповідь у вигляді повоєнної нерівності з урахуванням періодичності функції

π – arcsin a + 2πn < x < arcsin a + 2πn,

tgx>a

В системі координат малюємо одиничне коло, з виколотими значеннями
Будуємо лінію значень тангенса (дотична до одиничного кола в т.(1;0)); на яку переносимо шкалу значень.
На лінії значень тангенса ставимо значення а, що поділяє на дві частини: верхню (значення більші за а), нижню (менші за а) – наводимо хвилястою відповідну частину.
Через значення а і початок координат проводимо пряму, що розбиває одиничне коло на верхню та нижню частини, вибираємо відповідну верхню.
Позначаємо відповідний центральний кут та вертикальний до нього.
Визначаємо координати кінців дуги та записуємо відповідь у вигляді подвоєної нерівності з урахуванням періодичності функції.

arctg a + πn < x < + πn,

Для косинуса та котангенса алгоритми аналогічні (лінія значень косинуса – вісь Ох; лінія значень котангенса – дотична до одиничного кола в точці (0;1)).

Домашнє завдання.

Р.ІІ; §5, №3 с.127.

Лекція № 52-53

Тема:Тригонометричні рівняння. Деякі способи розв’язування тригонометричних рівнянь.

План:

Спосіб зведення до однієї тригонометричної функції (алгебраїчний спосіб)
Спосіб розкладання на множники
Спосіб розв’язування однорідних рівнянь
Спосіб введення допоміжного аргументу
Спосіб піднесення до квадрату
Графічний спосіб
Приклади розв’язування деяких інших видів тригонометричних рівнянь

Розглянемо окремо способи розв’язування деяких тригонометричних рівнянь на прикладі одного рівняння і спробуємо обґрунтувати доцільність використання кожного з них.

Розв’яжемо рівняння

sin x – cos x = 0. (1)

Спосіб зведення до однієї тригонометричної функції (алгебраїчний спосіб). Цим способом розв’язують рівняння, до складу яких входять різні тригонометричні функції одного і того самого аргументу. Використовуючи основні тригонометричні тотожності, всі функції виражають через одну функцію, а потім розв’язують алгебраїчне рівняння відносно цієї функції.

Отже, перенесемо cos x у праву частину рівняння і виразимо його через sin x за формулою

Дістанемо рівняння

(2)

Піднесемо обидві частини рівняння (2) до квадрата. Дістанемо або звідки Добудемо квадратний корінь з обох частин рівняння, використовуючи тотожність Маємо Розглянемо два найпростіших тригонометричних рівняння:

або

О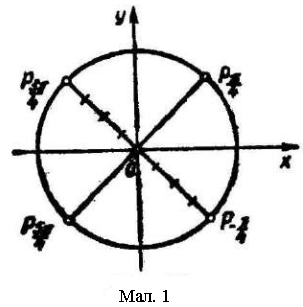 скільки ми виконували піднесення обох частин рівняння (2) до квадрата, то можливі порушення рівносильності, тобто рівняння а отже, і можуть мат сторонні розв’язки.

Щоб відкинути сторонні розв’язки, зробимо перевірку на відрізку завдовжки 2, зокрема на [0; 2], враховуючи, що найменшим додатним періодом синуса і косинуса є число 2. Для цього зручно використати одиничне коло. Позначимо на одиничному колі всі точки, які відповідають числам, що містяться у знайдених серіях розв’язків (мал.1).

Перша формула, якщо k = 0, 1, 2, дає точки

Друга формула, якщо k = 0, 1, 2, дає точки

Підставимо кожне із здобутих чисел у дане рівняння:

якщо то

Отже, дане рівняння задовольняють лише розв’язки з двох множин:

Їх можна записати однією формулою, якщо перетворити другу формулу так:

У першій серії до додають число 2n, а у другій – (2n+1). Парні і непарні числа утворюють множину цілих чисел. Тому об’єднана формула розв’язків матиме вигляд

Способом зведення до однієї функції можна розв’язувати, наприклад, такі рівняння: та ін.

Спосіб розкладання на множники. Під час розв’язування тригонометричних рівнянь цим способом усі члени рівняння переносять у ліву частину і подають утворений вираз у вигляді добутку. Далі використовують необхідну і достатню умови рівності нулю добутку тригонометричних виразів: добуток двох або кількох співмножників дорівнює нулю тоді і лише тоді, коли принаймні один із співмножників дорівнює нулю, а інші при цьому не втрачають смислу.

У даному рівнянні (1) всі члени містяться у лівій частині. Запишемо через і застосуємо формулу різниці синусів

Звідси Оскільки то Отже, а

Дістали ту саму множину розв’язків, що й під час розв’язування першим способом, але коротшим шляхом. Крім того, під час розв’язування не було порушення рівносильності рівнянь, тому в перевірці немає потреби.

Спосіб розв’язування однорідних рівнянь. Цей спосіб застосовують під час розв’язування однорідних тригонометричних рівнянь, тобто таких, у яких ліва частина є многочленом, у кожному члені якого сума показників степенів синуса і косинуса одного і того самого аргументу однакова, а права – нуль. У загальному випадку однорідне тригонометричне рівняння можна записати так:

Однорідне рівняння n-го степеня відносно синуса і косинуса розв’язують діленням обох частин на Проте попередньо слід довести, що Використаємо для цього метод доведення від супротивного. Припустимо, що Тоді, підставляючи у дане рівняння замість число 0, дістанемо звідки А це суперечить властивостям синуса і косинуса одного і того самого аргументу, оскільки якщо Поділивши на обидві частини однорідного рівняння, дістанемо алгебраїчне відносно функції тангенса рівняння

Дане рівняння однорідне. Доведемо, що Це так, бо якщо мала б виконуватись рівність а це неможливо для одного і того самого аргументу.

Поділимо обидві частини рівняння на Дістанемо або звідки або

Не слід думати, що під час розв’язування однорідних рівнянь завжди можна ділити на Наприклад, якщо у рівнянні поділити обидві частини на то можна загубити серію розв’язків Причина полягає в тому, що в цьому рівнянні може дорівнювати нулю, тому й треба розв’язувати способом розкладання на множники і т.д.

Спосіб введення допоміжного аргументу. Запишемо дане рівняння у вигляді Замінимо 1 на Дістанемо

Помножимо обидві частини рівняння на Дістанемо або Звідси

Спосіб уведення допоміжного аргументу застосовують під час розв’язування лінійних тригонометричних рівнянь, якими називаються рівняння виду Дане рівняння є окремим випадком лінійного.

Розглянемо у загальному випадку розв’язування лінійного тригонометричного рівняння способом уведення допоміжного аргументу. Винесемо за дужки з лівої частини рівняння Дістанемо

Очевидно, що і Крім того, Це означає, що коли матимемо

Підставимо у попереднє рівняння ці вирази. Дістанемо

або

За умови, що або останнє тригонометричне рівняння має розв’язок

де оскільки

Отже, перед розв’язуванням лінійного тригонометричного рівняння треба перевірити, чи виконується умова Зафіксуємо здобуту формулу при розв’язуванні даного рівняння:

(3)

Будемо користуватися нею під час розв’язування інших задач, пов’язаних з тригонометричними функціями.

Застосовуючи цей загальний спосіб розв’язування, зокрема здобуту формулу (3), до даного рівняння дістанемо бо Звідси

Лінійне тригонометричне рівняння можна розв’язати ще кількома способами. Зокрема, можна звести його до однорідного, ввівши заміну як множник с і замінивши та за формулами подвійного аргументу:

Можна також замінити і на тангенс половинного кута за формулами

Спосіб піднесення до квадрата. Рівняння (1) можна розв’язати способом піднесення обох частин до квадрата. Отже,

У цьому разі піднесення до квадрата не спричиняє появу сторонніх розв’язків.

Графічний спосіб. Запишемо дане рівняння у вигляді і введемо функції та Побудувавши в одній системі координат графіки цих функцій, знайдемо розв’язки рівняння як абсциси точок перетину графіків (мал.2).

Порівнюючи розглянуті способи розв’язування рівняння неважко зробити висновок, що найменш раціональним є перший (алгебраїчний) спосіб, який призводить до появи сторонніх розв’язків і потребує перевірки.

Розглянемо приклад рівняння, розв’язування якого вимагає виключення сторонніх розв’язків.

Приклад 1. Розв’язати рівняння

Розв’язання. Прирівнявши до нуля кожен із співмножників, розв’яжемо здобуті рівняння, а із знайдених розв’язків виключимо ті, при яких інші співмножники втрачають смисл:

О скільки синус існує для будь-яких аргументів, то із знайдених розв’язків слід виключити ті, при яких не існують і Для цього розкладемо формули, за допомогою яких записано розв’язки кожного з трьох рівнянь, на елементарні (елементарними називають формули розв’язків виду де 02) і зобразимо їх на одиничних колах (мал. 3). Це можна зробити, оскільки період 2 є спільним для всіх трьох співмножників.

Перевірка показала, що із 10 елементарних формул розв’язків, зображених на малюнках, шість виявилися сторонніми для даного рівняння (вони перекреслені), оскільки для таких чисел тангенс і котангенс не існують.

Отже, розв’язки рівняння запишемо у вигляді

Рівняння, що містять тригонометричні функції у знаменнику, як і дробові раціональні рівняння, зводять до виду Далі використовують необхідну і достатню умови рівності дробу нулю.

Наприклад, у рівнянні чисельник дробу дорівнює нулю, якщо але при цих значеннях втрачає смисл знаменник, бо tgх не існує.

Приклад 2. Розв’язати рівняння

Розв’язання.

Маємо:

З множини розв’язків x=k слід виключити ті, при яких знаменник перетворюється у нуль, тобто коли cosx перетворюється у -1. Відомо, що cosx дорівнює -1 при всіх непарних k. Отже, треба залишити лише розв’язки x=2n.

Множина розв’язків x=4n включається в множину x=2n. Розв’язками даного рівняння є x=2n.

Рівняння, до складу яких входять добутки sinsin, sincos, coscos, зручно розв’язувати за такими формулами:

Приклад 3. Розв’язати рівняння

Розв’язання.

Звідси маємо два рівняння:

Тригонометричні рівняння, до складу яких входять алгебраїчні суми виду або інші аналогічні комбінації аргументів, часто розв’язують, групуючи члени і застосовуючи формули додавання тригонометричних функцій. Але робити це слід так, щоб після перетворення у добуток кожної пари доданків з’являвся спільний множник. Далі рівняння розв’язують, розкладаючи його на множники.

Приклад 4. Розв’язати рівняння

Розв’язання. Згрупуємо члени так: Застосуємо формули суми і різниці синусів і використаємо властивість парності косинуса

Ще раз перетворимо у добуток суму косинусів

Звідси дістанемо три рівняння:

Остання множина розв’язків входить до множини Отже, розв’язками даного рівняння є числа

Тригонометричні рівняння, до складу яких входять парні степені функцій sinx і cosx, доцільно розв’язувати, понижаючи степінь функції за формулами

Приклад 5. Розв’язати рівняння

Розв’язання. Якщо зробити заміни то дістанемо рівняння або Звідси Маємо квадратне рівняння відносно cos2x. Розв’язуючи його способом розкладання на множники, дістанемо Звідси не має розв’язків, оскільки

Отже, розв’язками даного рівняння є числа Це рівняння можна було б розв’язати інакше, замінивши на а - на Після цього дістанемо квадратне рівняння відносно sinх. Та цей спосіб більш громіздкий. Під час розв’язування тригонометричних рівнянь слід пам’ятати про можливі випадки порушення рівносильності рівняння, тобто про втрату і появу сторонніх розв’язків. Зокрема, при піднесенні до квадрата обох частин рівняння можуть з’явитися сторонні розв’язки. Під час розв’язування однорідних рівнянь необґрунтоване ділення на може призвести до втрати розв’язків. Доводиться включати сторонні розв’язки і розв’язуючи рівняння, що містять добутки і дроби у лівій частині і нуль – у правій.

Наведемо ще два приклади втрати розв’язків.

Приклад 6. Розв’язати рівняння

Розв’язання. Це лінійне рівняння. Використаємо підстановки Дістанемо Оскільки то Звідси

Неважко перевірити, що дане рівняння задовольняють і числа х=(2n+1). Втрата розв’язків сталася внаслідок застосування підстановки і переходу до алгебраїчного рівняння відносно тангенса. Його не задовольняють числа, при яких не існує, тобто числа або х=(2n+1). Але ці числа задовольняють дане рівняння. Тому, використовуючи підстановку, яка виражає синус і косинус через тангенс половинного кута, необхідно перевіряти числа х=(2n+1). Якщо вони задовольняють дане рівняння, то їх слід приєднати до знайдених розв’язків. Остаточно запишемо розв’язок у вигляді

Приклад 7. Розв’язати рівняння

Розв’язання. Застосуємо формули

Дістанемо

Після спрощення маємо

При цих значеннях х не втрачає смислу і не перетворюється у нуль знаменник дробу. Проте неважко перевірити, що дане рівняння задовольняють також числа виду Втрата цих розв’язків сталася внаслідок застосування теореми додавання для функції тангенс. Формули тангенса суми і різниці двох чисел  і  виконуються лише за умови, що мають смисл вирази tg, tg, tg(+). Якщо то tgx не має смислу, тому ці розв’язки було втрачено. Якщо дане рівняння розв’язати за формулою суми тангенсів двох чисел, то вказані розв’язки не будуть втрачені.

В результаті розв’язування одного і того самого тригонометричного рівняння різними способами можна дістати різні загальні формули розв’язків рівняння. Їх еквівалентність можна довести, перетворивши формули та об’єднавши кілька формул в одну. Можна також довести рівність знайдених множин розв’язків, записавши у розгорнутому вигляді прогресії, n-м членом яких є формула розв’язку тригонометричного рівняння. Проте обидва ці способи громіздкі. Доцільно записати дане тригонометричне рівняння у вигляді f(x)=0, знайти найменший додатний період l функції у= f(x) і показати, що на проміжку [0;l] кожна з утворених формул дає одну і ту саму множину розв’язків. Зручним виявляється також геометричний спосіб доведення рівності множин розв’язків за допомогою одиничного кола. Якщо різні формули на одиничному колі дають однакові множини точок, що зображують окремі розв’язки рівняння, то ці множини рівні. Проте така геометрична інтерпретація можлива тільки тоді, коли періодом функції, що входить до лівої частини рівняння f(x)=0 (не обов’язково найменшим додатним), є число 2.

Домашнє завдання.

1) Р.ІІ; §2-3, с.126-127 №1 (14, 16, 18), №2 (рів.А №1-14диф.)

2) Р.ІІ; §2,4, с.127 №2 (рів.Б диференц.)