Лекція № 46

Тема: Формули зведення.

План:

1. Властивість періодичності тригонометричних функцій для обчислення будь-якого числового аргументу.

2. Формули зведення.

3. Алгоритм використання формул зведення при розв’язуванні вправ.

Властивість періодичності тригонометричних функцій будь-якого числового аргументу дає змогу звести обчислення їх значень до обчислення значень функції для аргументу від 0 до 2 (для синуса і косинуса) і від 0 до  (для тангенса і котангенса) за допомогою формул додавання.

Нехай, наприклад, треба обчислити cos, де << Запишемо  у вигляді =+, де 0<< За формулою (1) додавання для косинуса дістанемо: cos(+) = coscos - sinsin = - cos. Формула cos(+) = = - cos виконується при будь-якому  і називається формулою зведення (таблиця 1).

Щоб записати будь-яку формулу зведення, коли 0<< зручно користуватися такими правилами:

1) якщо кут  добудовується відносно вертикального діаметра (мал.1) (це кути, що відповідають числам ), то назва даної функції змінюється на кофункцію (синус на косинус, тангенс на котангенс і навпаки); якщо кут  добудовується відносно горизонтального діаметра (мал.2) (це кути, що відповідають числам ), то назва даної функції не змінюється;

2) перед утвореною функцією ставиться той знак, який має функція, що перетворюється за формулою зведення.

Мал. 1 Мал. 2

Таблиця 1

Домашнє завдання.

р.І; §10, п.2; зб. Капіносов С.

Лекція № 47

Тема: Тригонометричні формули суми, різниці двох кутів; подвійного аргументу. Сума, різниця синусів і косинусів.

План:

1. Формули тригонометричних функцій суми і різниці двох чисел:

а) sin(+) = sin cos + cos sin;

б) sin(-) = sin cos - cos sin;

в) cos(+) = cos cos - sin sin;

г) cos(-) = cos cos + sin sin;

д) tg(+) =

є) tg(-) =

2. Тригонометричні функції подвійного аргументу.

а) sin2 = 2sin cos;

б) cos2 = cos² - sin² = 2cos² - 1 = 1 - 2sin²;

в) tg2 =

3. Формули суми і різниці однойменних тригонометричних функцій

а) sin + sin = 2sin cos

б) sin - sin = 2sin cos

в) cos + cos = 2cos cos

г) cos - cos = - 2sin sin

д) tg + tg =

є) tg - tg =

Формули тригонометричних функцій суми і різниці двох чисел

sin(+) = sin cos + cos sin; (1)

sin(-) = sin cos - cos sin; (2)

cos(+) = cos cos - sin sin; (3)

cos(-) = cos cos + sin sin; (4)

tg(+) = (5)

tg(-) = (6)

Доведемо формулу (1), з якої неважко дістати решту.

Н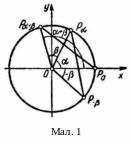 ехай  і  - будь-які числа. Виберемо на одиничному колі точки Р_, Р_-, Р_+, які отримують з точки Р₀ (1;0), повернувши її відповідно на кути , -, + (мал.1). Враховуючи означення синуса і косинуса, можна записати координати вибраних точок: Р_ (cos;sin), Р_- (cos(-);sin(-)), Р_+ (cos(+);sin(+)).

Хорди Р₀Р_+ і Р_- Р_ рівні, оскільки рівні відповідні їм дуги кола. Знайдемо довжини цих хорд за формулою відстані між двома точками

= (1 – cos(+))² + (sin(+))²;

= (cos(-) - cos)² + (sin(-) - sin)².

Оскільки Р₀Р_+ = Р_-Р_, то (Р₀Р_+)² = (Р_-Р_)². Тому (1 – cos(+))² + + (sin(+))² = (cos(-) - cos)² + (sin(-) - sin)².

Застосовуючи властивість парності косинуса і непарності синуса та формулу квадрата двочлена, дістанемо

1 – 2cos(+) + cos²(+) + sin²(+) = cos2 - 2coscos + cos² + sin² + + 2sinsin + sin².

Використовуючи основну тригонометричну тотожність, маємо

2 – 2cos(+) = 2 – 2coscos + 2sinsin.

Виразивши з останньої рівності cos(+), дістанемо формулу (1) для косинуса суми двох аргументів

cos(+) = coscos - sinsin.

Формулу (б) дістанемо, замінивши у (1)  на - і скориставшись парністю косинуса і непарністю синуса,

cos(+(-)) = coscos(-) - sinsin(-),

cos(-) = coscos + sinsin.

Формулу додавання для синуса неважко дістати з формули (1) і формули зведення sinx = cos

Вказану формулу зведення можна дістати і з формули (1), поклавши Справді, cos = cos cos + sin sin = 0cos + 1sin = sin.

Отже, cos = sin. (7)

Замінивши у формулі (7)  на , дістанемо

або

Отже,

Виразимо sin(+), скориставшись формулою (7) выдносно числа (+) у зворотному порядку:

Отже, дістали формулу (3)

cos(+) = cos cos - sin sin.

Формулу (4) дістанемо, замінивши у формулі (3)  на - і скориставшись парністю косинуса і непарністю синуса,

звідки

Формулу додавання для тангенса можна дістати за означеннями тангенса і формулами додавання для синуса і косинуса:

Розділивши почленно чисельник і знаменник правої частини на вираз (поясніть чому ві не дорівнює 0), дістанемо:

Отже, дістали формулу (5)

Якщо замінити у формулі (5)  на - і врахувати непарність тангенса, то

Застосуємо формулу (4) до доведення зростання функції на проміжку користуючись означенням зростаючої функції. Нехай і х₂>x₁. Доведемо, що різниця додатна.

Справді,

оскільки за умовою 0< х₂–x₁<. Тоді cos х₂>0, cos х₁>0, sin(х₂–x₁)>0.

Тригонометричні функції подвійного аргументу. Це формули, які виражають функції 2α через функції аргументу α. Їх можна здобути з формул додавання.

Поклавши β = α у формулі (3), дістанемо формулу синуса подвійного аргументу

sin2 = 2sincos. (8)

З формули (1), якщо β = α, дістанемо формулу косинуса подвійного аргументу

cos2 = cos² - sin². (9)

Якщо змінити за допомогою основної тригонометричної тотожності sin² + cos² = 1 функцією cos на sin або sin на cos, то матимемо ще дві формули для cos2:

cos2 = 2cos² -1, cos2 = 1 - sin².

З формули (5), якщо β = α, маємо:

Формули (8) і (9) виконуються для будь-яких значень аргументу, а формула (10) – лише для тих, для яких існують tg2α, tgα і 1 - tg²  0.