Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания признака).
Таблица 1 – Расчетная таблица
Номер п/п |
Выборка, |
Вариацион-ный ряд, xi |
X |
X^2 |
X^3 |
X^4 |
1 |
18,9141 |
15,9393 |
-0,11708 |
0,013708 |
-0,00160498 |
0,00018791 |
2 |
20,7026 |
16,388 |
1,671418 |
2,793638 |
4,669337057 |
7,80441401 |
3 |
18,9174 |
16,7852 |
-0,11378 |
0,012946 |
-0,00147306 |
0,00016761 |
4 |
19,9372 |
17,1609 |
0,906018 |
0,820869 |
0,743721742 |
0,67382529 |
5 |
18,9678 |
17,3142 |
-0,06338 |
0,004017 |
-0,00025462 |
1,6139E-05 |
6 |
21,1771 |
17,4023 |
2,145918 |
4,604964 |
9,881875272 |
21,205694 |
7 |
18,4972 |
17,6722 |
-0,53398 |
0,285137 |
-0,15225791 |
0,08130298 |
8 |
19,208 |
17,6973 |
0,176818 |
0,031265 |
0,005528145 |
0,00097748 |
9 |
15,9393 |
17,7077 |
-3,09188 |
9,559734 |
-29,5575704 |
91,3885199 |
10 |
20,3087 |
17,7349 |
1,277518 |
1,632052 |
2,084976114 |
2,66359452 |
11 |
17,6722 |
17,8107 |
-1,35898 |
1,846832 |
-2,50981155 |
3,41078872 |
12 |
16,388 |
17,9211 |
-2,64318 |
6,986411 |
-18,466356 |
48,8099399 |
13 |
20,2339 |
18,3071 |
1,202718 |
1,446531 |
1,739768375 |
2,09245074 |
14 |
18,9226 |
18,4972 |
-0,10858 |
0,01179 |
-0,00128019 |
0,00013901 |
15 |
19,7789 |
18,7929 |
0,747718 |
0,559082 |
0,41803583 |
0,31257291 |
16 |
17,4023 |
18,835 |
-1,62888 |
2,653257 |
-4,32184187 |
7,03977043 |
17 |
20,1476 |
18,8361 |
1,116418 |
1,246389 |
1,391491283 |
1,55348592 |
18 |
18,3071 |
18,8797 |
-0,72408 |
0,524295 |
-0,37963239 |
0,27488498 |
19 |
16,7852 |
18,9141 |
-2,24598 |
5,044435 |
-11,3297105 |
25,4463259 |
20 |
18,835 |
18,9174 |
-0,19618 |
0,038487 |
-0,00755053 |
0,00148128 |
21 |
21,6077 |
18,9226 |
2,576518 |
6,638445 |
17,10407305 |
44,0689521 |
22 |
19,0824 |
18,9302 |
0,051218 |
0,002623 |
0,000134359 |
6,8816E-06 |
23 |
19,7563 |
18,9678 |
0,725118 |
0,525796 |
0,381264227 |
0,27646155 |
24 |
17,7349 |
18,9749 |
-1,29628 |
1,680347 |
-2,1782036 |
2,82356612 |
25 |
19,3174 |
19,0387 |
0,286218 |
0,081921 |
0,023447191 |
0,00671101 |
26 |
21,5386 |
19,0824 |
2,507418 |
6,287145 |
15,76450061 |
39,5281926 |
27 |
18,7929 |
19,0893 |
-0,23828 |
0,056778 |
-0,01352925 |
0,00322378 |
28 |
20,4599 |
19,0949 |
1,428718 |
2,041235 |
2,916349363 |
4,16664083 |
29 |
18,8361 |
19,1582 |
-0,19508 |
0,038057 |
-0,00742423 |
0,00144833 |
30 |
17,3142 |
19,208 |
-1,71698 |
2,948027 |
-5,06170962 |
8,6908643 |
31 |
17,8107 |
19,2241 |
-1,22048 |
1,489576 |
-1,81800108 |
2,21883759 |
32 |
19,5773 |
19,3174 |
0,546118 |
0,298245 |
0,162876892 |
0,08895 |
33 |
17,6973 |
19,4469 |
-1,33388 |
1,779241 |
-2,3732978 |
3,16569921 |
34 |
20,7187 |
19,489 |
1,687518 |
2,847717 |
4,805573697 |
8,10949211 |
35 |
19,5645 |
19,5645 |
0,533318 |
0,284428 |
0,15169062 |
0,08089934 |
36 |
19,1582 |
19,5773 |
0,127018 |
0,016134 |
0,002049254 |
0,00026029 |
37 |
18,9302 |
19,7563 |
-0,10098 |
0,010197 |
-0,00102975 |
0,00010399 |
38 |
19,2241 |
19,7789 |
0,192918 |
0,037217 |
0,007179898 |
0,00138513 |
39 |
20,3843 |
19,9372 |
1,353118 |
1,830928 |
2,477462069 |
3,35229852 |
40 |
19,0893 |
20,1476 |
0,058118 |
0,003378 |
0,000196305 |
1,1409E-05 |
41 |
18,8797 |
20,2081 |
-0,15148 |
0,022947 |
-0,00347603 |
0,00052656 |
42 |
18,9749 |
20,2339 |
-0,05628 |
0,003168 |
-0,00017828 |
1,0034E-05 |
43 |
19,4469 |
20,3087 |
0,415718 |
0,172821 |
0,07184499 |
0,02986726 |
44 |
17,7077 |
20,3843 |
-1,32348 |
1,751605 |
-2,31821716 |
3,06811869 |
45 |
17,1609 |
20,4599 |
-1,87028 |
3,497955 |
-6,54216182 |
12,2356875 |
46 |
19,489 |
20,7026 |
0,457818 |
0,209597 |
0,095957426 |
0,04393104 |
47 |
17,9211 |
20,7187 |
-1,11008 |
1,232282 |
-1,36793412 |
1,51851904 |
48 |
19,0949 |
21,1771 |
0,063718 |
0,00406 |
0,000258694 |
1,6483E-05 |
49 |
19,0387 |
21,5386 |
0,007518 |
5,65E-05 |
4,2492E-07 |
3,1945E-09 |
50 |
20,2081 |
21,6077 |
1,176918 |
1,385136 |
1,630191466 |
1,91860168 |
Построение интервального статического ряда:
Все наблюдаемые значения ξ находятся на отрезке [Xmin;Xmax]. Разобьём этот отрезок на k интервалов. k находим по формуле:
k=1+3,322log10n= 6,643978
Полученное значение k округляем до наибольшего целого, при этом учитываем что величина k должно выполнятся неравенство 5≤ k ≤15
Размах Выборки:
Xmax=21,6077
Xmin= 15,9393
Найдем размах выборки
21,6077- 15,9393 = 5,6684
Длинна h одной ячейки вычисляется по формуле:
h=R/k
h=
= 0,853164
где R – размер выборки.
Теперь вычисляем границы ячеек:
С1=xmin, c2=c1+h, c3=c2+h, …, ck+1=ck+h(ck+1≥xmax).
15,9393
=
15,9393+0,853164=
16,79246
=16,79246+0,853164=
17,64563
=17,64563+0,853164=
18,49879
=18,49879+0,853164=
19,35195
=
19,35195+0,853164=
20,20512
=
20,20512+0,853164=
21,05828
=
21,05828+ 0,853164=
21,91144
Составим таблицу 1.1
Таблица 1.1 – Статистический закон распределения непрерывной случайной величины
ячейки |
частоты |
относительные частоты |
[15,9393;17,1609) |
3 |
0,06 |
[17,1609;17,6722) |
3 |
0,06 |
[17,6722;18,7929) |
8 |
0,16 |
[18,7929;19,4469) |
18 |
0,36 |
[19,4469;20,2081) |
8 |
0,16 |
[20,2081;21,1771) |
7 |
0,14 |
[21,1771;21,6077) |
3 |
0,06 |
В таблице 1.1:
Частота – количество элементов в выборке, попадающий в заданную ячейку.
Относительные чистоты – это частное частоты и объёма выборки.
Постройка гистограммы:
На горизонтальные оси откладываются границы сi затем на каждом интервале строятся прямоугольники высотой mi/(nh), i=1,k
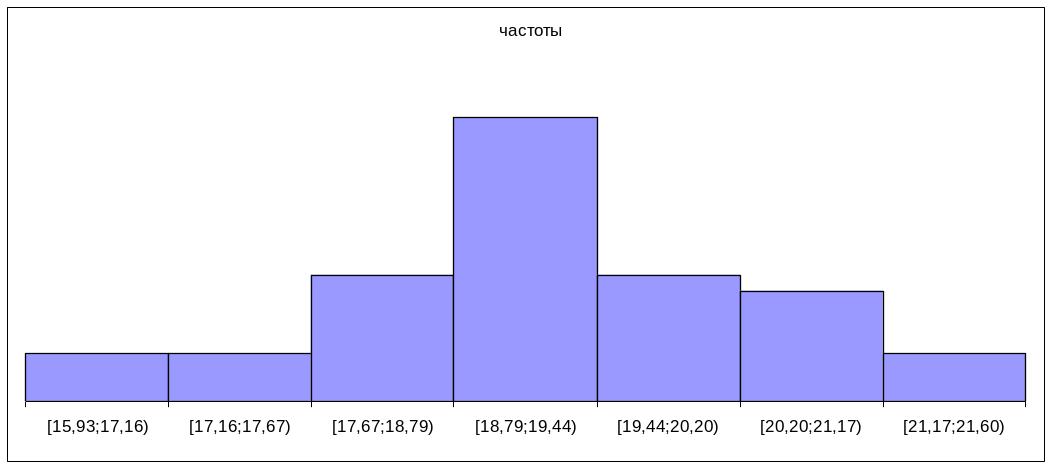
Рисунок 1.1 – Графическое изображение статистического закона распределения непрерывной случайной величины
Вычисление оценок числовых характеристик:
Название характеристики |
Теоретическое значение |
Оценка |
Математическое ожидание |
18 |
19,031182 |
Мода |
18 |
18,92537234 |
Медиана |
18 |
19,06055 |
Дисперсия |
1 |
1,577406189 |
Среднее квадротическое отклонение |
1 |
1,255948323 |
Область допускаемых значений (размах) |
(-∞;+∞) |
(15,23387;22,88723) |
Коэффициент вариации |
0,055555556 |
0,065994236 |
Коэффициент асимметрии |
0 |
-0,234832618 |
Коэффициент эксцесса |
0 |
-0,201524123 |
В качестве оценки
математического
ожидания
используется среднее арифметическое
наблюденных значений. Эта статистика
называется выборочным
средним.
.
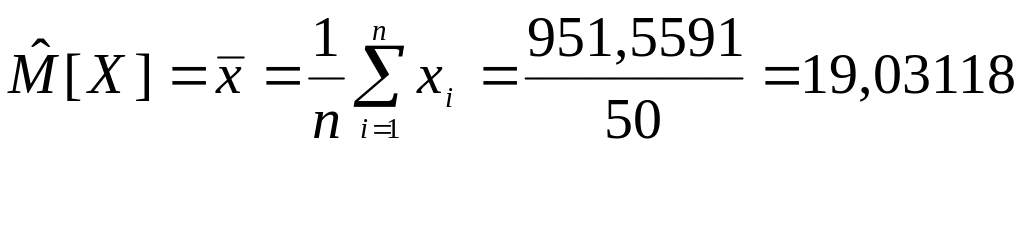Для оценивания
по выборочным данным моды распределения,
используется то значение сгруппированного
статистического ряда
,
которому соответствует наибольшее
значение частоты. По интервальному
статистическому ряду определяется
модальный интервал, в который попало
наибольшее
число элементов выборки,
и в качестве точечной оценки моды может
использоваться среднее значение этого
интервала.
.
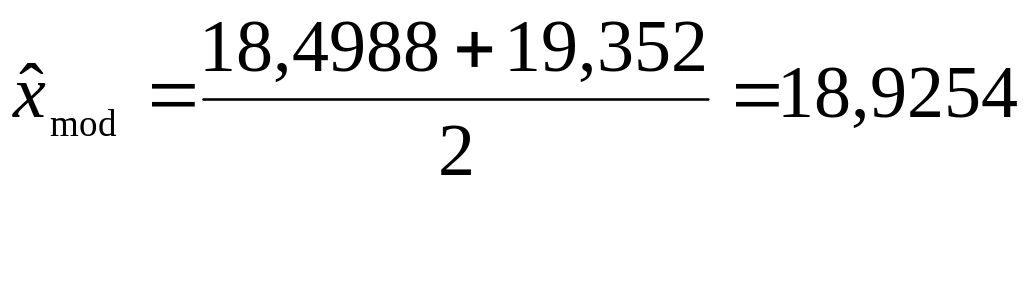Для определения
выборочного значения медианы используется
вариационный ряд. В качестве оценки
медианы
принимают средний (т. е.
-й)
член этого ряда, если значение n –
нечётно и среднее арифметическое между
двумя средними (т. е. между
-м
и
-м)
членами этого ряда, если n –
чётно. В нашем случае объем выборки
=
50 - четное, т.е. в качестве оценки медианы
примем
=
.
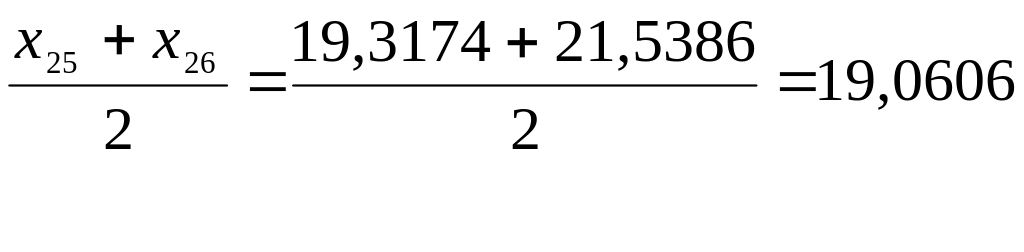В качестве оценки дисперсии используется статистика
=
.
Оценка среднего квадратичного отклонения
=
Оценка коэффициента вариации
Оценка коэффициента асимметрии
.
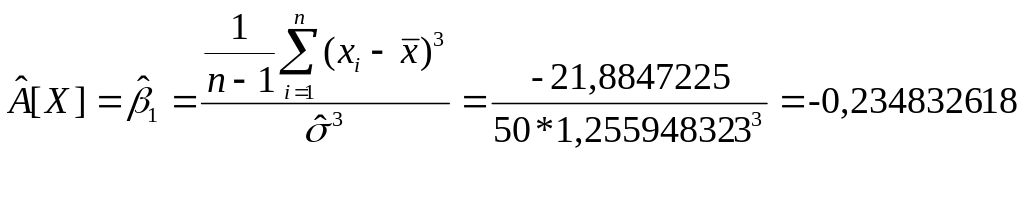Оценка коэффициента эксцесса
.
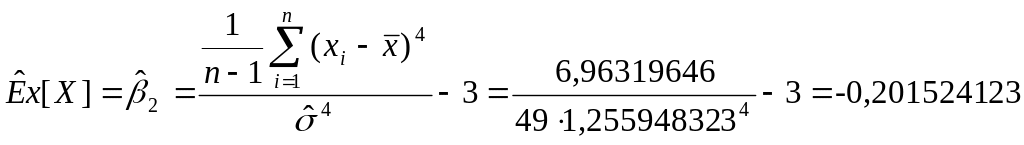