Государственное образовательное учреждение

высшего профессионального образования

“Санкт-Петербургский государственный политехнический университет”

Кафедра

управления конструкторско-технологическими инновациями

Отчет о лабораторной работе № 5.

Тема: Интерполяция дискретных данных

Студент гр. 2049/1 ________ Федорова Ю.К.

_{(подпись)}

Преподаватель ________ Кожанова Ю.В.

_{(подпись)}

Дата:

10.11.11

Санкт-Петербург

2011

Цель работы познакомиться с методами решения задачи интерполяции дискретных данных. Научиться пользоваться операторами интерполяции программы MathCAD.

Теоретические сведения:

При обработке экспериментальных данных, аппроксимации сложных функций возникают задачи выбора непрерывной функции, точно проходящей через заданные точки. При помощи этой функции можно получить дополнительные данные при промежуточных значениях аргумента. Такая операция называется интерполированием. Она является частным случаем аппроксимации. В общем случае при аппроксимации данных не требуется, чтобы значения функции точно совпадали с исходными данными.

Решение задачи интерполирования не является однозначным. Решение может быть получено при помощи различного вида функций. Можно соединить соседние точки прямыми линиями и использовать их для расчета промежуточных значений. Такая методика называется кусочно-линейной интерполяцией. Если весь промежуток интерполяции разделить на трёхточечные интервалы, то можно выполнить кусочно-квадратичную интерполяцию.

Разрывы непрерывности производных в узловых точках можно устранить при помощи сплайн-интерполяции. Кубическая интерполяция позволяет построить кривую, проходящую через заданные точки, таким образом, чтобы первые и вторые производные были бы непрерывными во всех точках. Такая кривая может быть построена разделением промежутка интерполяции на трехточечные интервалы, внутри которых записываются полиномы третьей степени, проходящие через эти точки. Эти полиномы затем соединяются вместе и образуют общую кривую.

Интерполяция обычными полиномами обеспечивает непрерывность производных во всех узлах, кроме граничных, и заключается в нахождении полинома низшей степени, принимающего заданное значение в исходных точках. Обычный полином

в узлах интерполяции x₀,x₁,...x_n должен точно совпадать со значениями функции y₀,y₁,...y_n. Как известно, существует единственный полином степени не выше n, принимающий в точках x₀,x₁...x_n заданные значения. Поэтому m=n, при этом число узлов интерполирования на единицу больше, чем степень полинома. Степень полинома равна числу интервалов, на которые разделяется весь промежуток интерполирования. Коэффициенты a_i полинома Q_n(x) можно определить различными способами.

1.Из решения системы уравнений

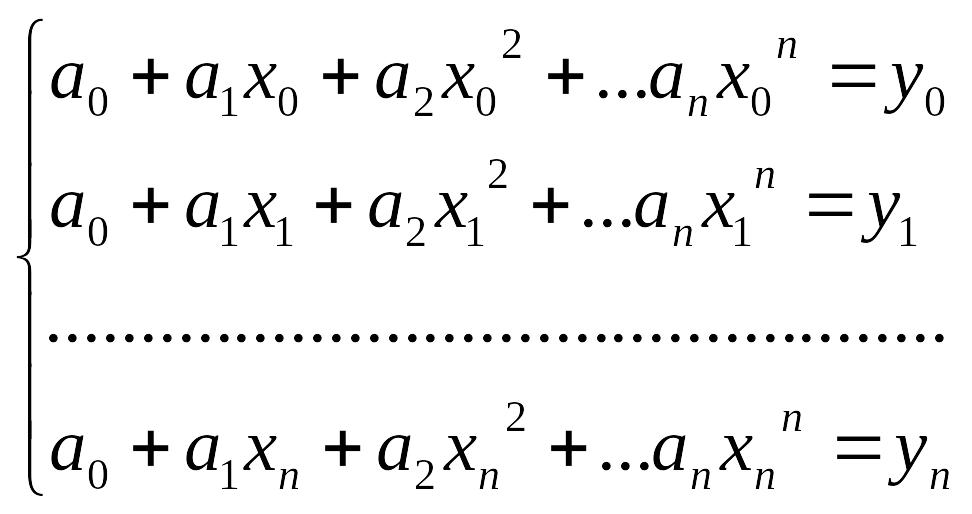_(5.1)

Порядок системы (5.1) равен числу узлов интерполирования, т.е. n+1.Решение системы (5.1) может быть получено способом Крамера с помощью определителей или способом Гаусса путем исключения переменных.

2.По формуле Лагранжа, позволяющей определить полином Q_n(x) при произвольных узлах интерполяции.

Q_n(x)= _(5.2)

3.По формуле Ньютона, позволяющей определить полином Q_n(x) при равноотстоящих с шагом h узлах интерполирования.

(5.3)

При определении значений функции f(x) в точке x по формулам Лагранжа или Ньютона в качестве начальной точки выгодно брать ближайший к x узел интерполирования. Тогда первое слагаемое в этой формуле будет главным членом, а остальные слагаемые будут носить характер поправки. При небольшом числе узлов алгоритм (рис.5.1) может быть реализован вручную. Но для большого количества узлов лучше записать алгоритм в виде программы на одном из языков программирования.

Рис.5.1. Схема вычисления интерполяционного полинома

по формуле Лагранжа

На рис.5.2 на языке Паскаль записана программа, реализующая алгоритм (рис.5.1). Программа рассчитывает значение полинома n- порядка в произвольных точках по n+1 значениям x и y.

В программе, использующей метку, рассчитывается функция Лагранжа L. Исходные данные: n - порядок полинома, x_i и y_i - исходные точки при i=0,1,2...n , промежуточное значение x. Программа выводит полученное значение y вместе заданным значением x. Её можно использовать в качестве подпрограммы в сложных программах математического моделирования, когда требуется интерполяция дискретных данных.

Подпрограмма на языке программирования Mathcad (рис.5.3), реализующая тот же алгоритм при трехточечных исходных данных оформлена в виде подпрограммы-скаляра, возвращающего значение интерполяционного полинома при произвольном значении аргумента z.

Для использования подпрограммы в документе Mathcad в качестве глобальных переменных нужно задать трёхточечные векторы исходных данных. Два вложенных цикла for и опрератор ветвления if позволяют рассчитать коэффициенты a_i и b_i в элементах суммы функции Лагранжа, а также рассчитать её значение.

Рис.5.2. Программа на языке Паскаль для

интерполяции по формуле Лагранжа.

Рис.5.3.Подпрограмма на языке программирования Маthcad для интерполяции по формуле Лагранжа.

Ввод исходных данных:

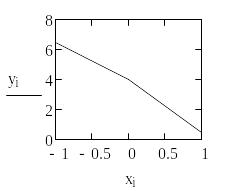
Воспользуемся графическими возможностями MathCAD для визуализации исходных данных. По оси х отложим дискретные значения x_i, а по оси y соответственно y_i.

Кусочно-линейная интерполяция исходных данных средствами MathCAD

Сначала будем решать задачу интерполяции, используя формулу Лагранжа и подпрограмму для определения промежуточных точек.

Подпрограмма позволяет получить все необходимые значения функции, в том числе и при промежуточных значениях аргумента.

Запишем имеющиеся данные при помощи двух пар векторов. Векторы z₁ и f₁ соответствуют исходным данным, а векторы z и f полному набору точек с учетом полученных промежуточных значений.

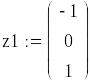
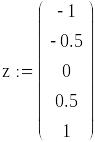
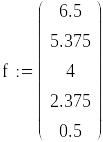
Представим записанные векторы в графическом виде с использованием автоматической кусочно-линейной интерполяции MathCAD.