
- •Физика по направлению подготовки
- •Программа
- •Реализация компетенции ок(2)
- •Реализация компетенций ок4 и ок8.
- •Учебный план курса План лекционных занятий
- •План лабораторных работ
- •План практических занятий
- •Вопросы, вынесенные на самостоятельную подготовку.
- •Вопросы к зачету
- •Основная и дополнительная литература
- •Лабораторные работы
- •Механика Лабораторная работа №1 «Изучение колебаний математического маятника»
- •I. Цель работы
- •II. Теоретическая часть
- •III. Порядок проведения экспериментальных измерений.
- •IV. Обработка результатов измерений в программе Microsoft Excel.
- •Контрольные вопросы
- •Лабораторная работа № 2 «Изучение колебаний физического маятника»
- •Цель работы
- •Теоретическая часть
- •Порядок проведения экспериментальных измерений
- •Обработка результатов измерений в программе Microsoft Excel
- •Контрольные вопросы
- •Лабораторная работа № 3 «Изучение колебаний пружинного маятника»
- •Цель работы:
- •Теоретическая часть
- •Порядок проведения измерений
- •Обработка результатов измерений в программе Microsoft Excel
- •Контрольные вопросы
- •Лабораторная работа № 4 «Определение моментов инерции тел методом крутильных колебаний»
- •Цель работы:
- •Теоретическая часть.
- •Порядок проведения экспериментальных измерений
- •Обработка результатов измерений в программе Microsoft Excel
- •Контрольные вопросы:
- •Электричество и магнетизм. Лабораторная работа № 5 Экспериментальная проверка закона Ома и определение сопротивления проводника заданной длины в цепи постоянного тока
- •I. Цель лабораторной работы
- •II. Теоретическая часть
- •III. Порядок проведения эксперимента.
- •IV. Обработка результатов измерений в программе Microsoft Excel
- •Результаты замеров тока и напряжения
- •Окончательный вид таблицы №1
- •Окончательный вид таблицы №2
- •V. Определение зависимости сопротивления проводника заданной длины в цепи постоянного тока
- •Лабораторная работа № 6 Экспериментальное определение ёмкости конденсатора
- •I. Цель лабораторной работы
- •II. Теоретическая часть
- •III. Порядок проведения эксперимента.
- •IV. Обработка результатов измерений
- •Результаты замеров тока и времени при разрядке конденсатора
- •Результаты обработки экспериментальных данных исследуемого конденсатора
- •Зависимость выражения от времени t
- •Лабораторная работа № 7 Явление электромагнитной индукции. Исследование магнитного поля соленоида
- •I. Цель лабораторной работы
- •II. Теоретическая часть
- •III. Порядок проведения экспериментальных измерений.
- •Внешние витки; 2- соленоид; 3- внутренние витки; 4- генератор сигналов; 5- осциллограф; 6- коммутатор витков; b- магнитный поток.
- •IV. Обработка результатов измерений в программе Microsoft Excel
- •Результаты замеров частоты сигнала и напряжения эдс во внутреннем витке
- •Окончательный вид таблицы №3
- •Окончательный вид таблицы №4
- •Результаты замеров напряжения эдс на внутренних витках
- •Окончательный вид таблицы №7
- •Окончательный вид таблицы №9
- •Лабораторная работа № 8 Экспериментальное определение удельного сопротивления проводника в цепи постоянного тока
- •I. Цель лабораторной работы
- •II. Теоретическая часть
- •III. Порядок проведения эксперимента.
- •IV. Обработка результатов измерений
- •Результаты обработки замеров диаметра исследуемого проводника
- •Результаты замеров тока и напряжения в исследуемом проводнике
- •Результаты вычисления удельного сопротивления исследуемого проводника длиной 800 мм
- •Обработка результатов замеров диаметра исследуемого проводника
- •Результаты замеров тока и напряжения в исследуемом проводнике
- •Результаты вычисления удельного сопротивления исследуемого проводника длиной 400 мм
- •VI.4. Определение материала, из которого изготовлен исследуемый проводник
- •Оптика Лабораторная работа № 9 Изучение дифракции света на щели
- •I. Цель работы
- •II. Теоретическая часть
- •III. Порядок проведения эксперимента.
- •IV. Обработка результатов измерений
- •Результаты замеров и l, занесённые в Excel
- •Лабораторная работа № 10 Измерение длины волны света с помощью дифракционной решетки
- •I. Цель работы
- •II. Теоретическая часть
- •III. Порядок проведения эксперимента.
- •IV. Обработка результатов измерений
- •Результаты замеров и l, занесённые в Excel
- •Контрольные вопросы
- •Лабораторная работа № 11 Изучение явления поляризации
- •Цель работы:
- •Теоретическая часть
- •Порядок проведения измерений
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 12 Изучение естественного вращения плоскости поляризации
- •Цель работы
- •Теоретическая часть
- •Описание установки
- •Перед проведением измерений комплекс лко-5 требует настройки.
- •Порядок проведения эксперимента Определение угла поворота плоскости поляризации
- •Обработка результатов измерений
- •Заключение.
- •Контрольные вопросы
- •Рекомендуемая литература.
- •Методические указания к решению задач.
- •Механика;
- •Молекулярная физика и термодинамика;
- •Электричество и магнетизм;
- •Механические и электромагнитные колебания и волны;
- •Волновая и квантовая оптика;
- •Квантовая физика, физика атома;
- •Домашние задания.
- •Механика;
- •Молекулярная физика и термодинамика;
- •Механические и электромагнитные колебания и волны;
- •Электричество и магнетизм;
- •Волновая и квантовая оптика;
- •Элементы ядерной физики и физики элементарных частиц
Механические и электромагнитные колебания и волны;
Задача №6
Магнитный
момент ![]() контура
с током ориентирован в однородном
внешнем магнитном поле
контура
с током ориентирован в однородном
внешнем магнитном поле ![]() так,
как показано на рисунках. Положение
контура устойчиво и момент сил, действующих
на него, равен нулю в случае ...
так,
как показано на рисунках. Положение
контура устойчиво и момент сил, действующих
на него, равен нулю в случае ...
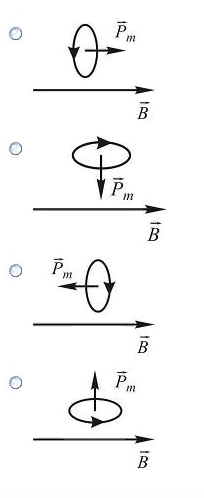
РЕШЕНИЕ (задача №6)
Вращающий
момент, действующий на контур с током
в магнитном поле, равен векторному
произведению магнитного момента ![]() m
контура и магнитной индукции
m
контура и магнитной индукции ![]() поля.
т.е.
поля.
т.е. ![]() .
Модуль вращающего момента равен М
= рmВ
sinα
,
где
α
-
yтол
между векторами
и
.
Из этой формулы следует, что вращающий
момент равен нулю и контур с током
находится в равновесии в однородном
магнитном поле в двух случаях: если
вектор
,
сонаправлен
вектору
(α
=0) и если вектора
и
направлены в противоположные стороны
(α
=π).
В первом случае равновесие рамки -
устойчивое, т.к. при отклонении контура
из положения, в котором α
=0. возникает момент M
сил Ампера, возвращающих контур в
положение равновесия. Во втором случае
контур находится в неустойчивом
равновесии, т.к. при любом отклонении
его от этого положения возникает момент
M
сил
Ампера, который вызывает дальнейшее
отклонение контура от положения α
=π.
Итак, положение рамки устойчиво и момент
сил. действующих на нее. равен нулю в
случае, показанном на рис.
.
Модуль вращающего момента равен М
= рmВ
sinα
,
где
α
-
yтол
между векторами
и
.
Из этой формулы следует, что вращающий
момент равен нулю и контур с током
находится в равновесии в однородном
магнитном поле в двух случаях: если
вектор
,
сонаправлен
вектору
(α
=0) и если вектора
и
направлены в противоположные стороны
(α
=π).
В первом случае равновесие рамки -
устойчивое, т.к. при отклонении контура
из положения, в котором α
=0. возникает момент M
сил Ампера, возвращающих контур в
положение равновесия. Во втором случае
контур находится в неустойчивом
равновесии, т.к. при любом отклонении
его от этого положения возникает момент
M
сил
Ампера, который вызывает дальнейшее
отклонение контура от положения α
=π.
Итак, положение рамки устойчиво и момент
сил. действующих на нее. равен нулю в
случае, показанном на рис.
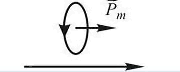
Волновая и квантовая оптика;
Задача №7.
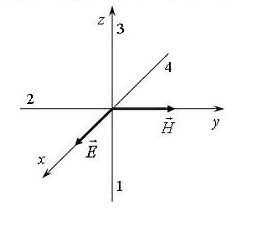
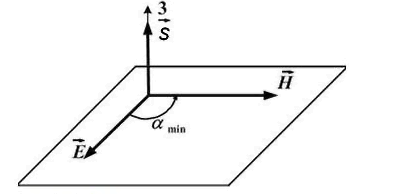
На
рисунке показана ориентация векторов
напряженности электрического (![]() )
и
магнитного (
)
и
магнитного (![]() )
полей
в электромагнитной волне. Вектор
плотности потока энергии электромагнитного
поля ориентирован в направлении ...
)
полей
в электромагнитной волне. Вектор
плотности потока энергии электромагнитного
поля ориентирован в направлении ...
4
3
1
2
РЕШЕНИЕ (задача №7)
Плотность
потока энергии электромагнитного поля
- вектор, называемый вектором Умова -
Пойнтинга, - определяется в векторной
форме как ![]() ,
где
,
где ![]() и
и
![]() – соответственно векторы напряженностей
электрической и магнитной составляющих
электромагнитной волны. Векторы
– соответственно векторы напряженностей
электрической и магнитной составляющих
электромагнитной волны. Векторы ![]() ,
,
являются
правой упорядоченной тройкой векторов.
,
,
являются
правой упорядоченной тройкой векторов.
На
рисунке показано, как найти направление
результирующего вектора ![]() векторного
произведения векторов
векторного
произведения векторов ![]() и
и ![]() .
.
Д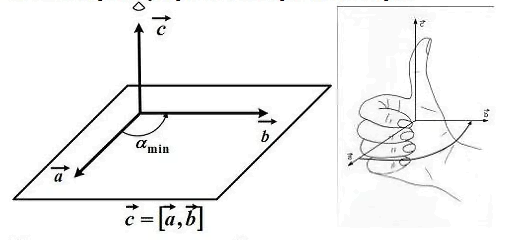 ля
нашего случая:
ля
нашего случая:
Для нашего случая:
![]()
Вектор
![]() направлен вдоль оси Z.
т.е. ориентирован в направлении 3.
направлен вдоль оси Z.
т.е. ориентирован в направлении 3.
Квантовая физика, физика атома;
Задача №8.
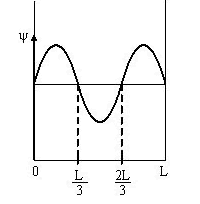
Если ψn(х) - функция электрона в одномерном потенциальном ящике шириной L с бесконечно высокими стенками имеет вид. указанный на рисунке, то вероятность обнаружить электрон на участке L/6 < х < L/2 равна ...
1/3
5/6
2/3
1/2
РЕШЕНИЕ (задачи №8)
Вероятность
обнаружить микрочастицу в интервале
(а,b)
для
состояния, характеризуемого определенной
ψn
-функцией, равна W
= ![]() .
Используя
геометрический смысл интеграла, эту
вероятность можно найти как отношение
площади под кривой зависимости |ψn(х)|2
в
интервале (а,b)
к
площади под кривой во всем интервале
существования |ψn(х)|2,
т.е. в интервале (0,L).
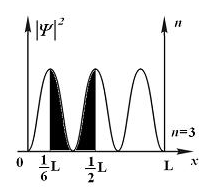
Кривая
зависимости |ψn(х)|2
от
х
представлена
на рисунке, где вероятность обнаружить
электрон на участке
.
Используя
геометрический смысл интеграла, эту
вероятность можно найти как отношение
площади под кривой зависимости |ψn(х)|2
в
интервале (а,b)
к
площади под кривой во всем интервале
существования |ψn(х)|2,
т.е. в интервале (0,L).
Кривая
зависимости |ψn(х)|2
от
х
представлена
на рисунке, где вероятность обнаружить
электрон на участке ![]() соответствует доле «закрашенной»
площади от всей площади под кривой (см.
рис.). т.е.
соответствует доле «закрашенной»
площади от всей площади под кривой (см.
рис.). т.е.
![]() .
.
Элементы ядерной физики и физики элементарных частиц
Задача №9.
В
ядерной реакции +![]() e→
+ X
буквой
X
обозначена
частица …
e→
+ X
буквой
X
обозначена
частица …
нейтрон
электрон
протон
позитрон
РЕШЕНИЕ (задача №9)
Из законов сохранения массового числа и зарядового числа следует, что заряд частицы равен нулю, а массовое число равно 1. Следовательно, буквой X обозначен нейтрон.
ПРИЛОЖЕНИЕ №3
