Indiferenční křivka:

Příklad: Užitkové funkce z preferencí

Složitější - jaké kombinace statků odpovídají chování spotřebitele pro

dané preference.

Dokonalé substituty (modré a červené tužky)

• Důležitý je pouze celkový počet tužek, takže např. u(x₁, x₂) = x₁ + x₂ popisuje tyto preference.

• Můžeme použít libovolnou monotónní transformaci, např. ln(x₁ + x₂).

Dokonalé komplementy (levé a pravé boty)

• Důležité je minimum levých a pravých bot, takže např. u(x₁, x₂) = min{x₁, x₂} popisuje tyto preference.

• Pokud nespotřebovávám statky v poměru 1:1, užitková funkce je u(x₁,x₂) = min{ax₁, bx₂}, kde a a b jsou pozitivní konstanty.

Příklad: Užitkové funkce z preferencí (pokračování)

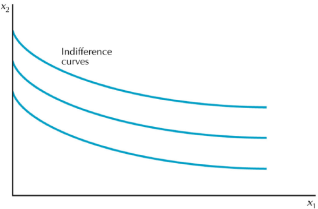
Kvazilineární preference

• Indiferenční křivky jsou vertikálně paralelní (viz Figure 4.4).

• Nijak zvlášť realistické, ale snadno se s nimi pracuje.

• Užitková funkce má tvar u(x₁,x₂) = v(x₁) + x₂.

• Konkrétní tvary: u(x₁x₂) = Xi + x₂ nebo u(x₁x₂) = lnx₁ + x₂.

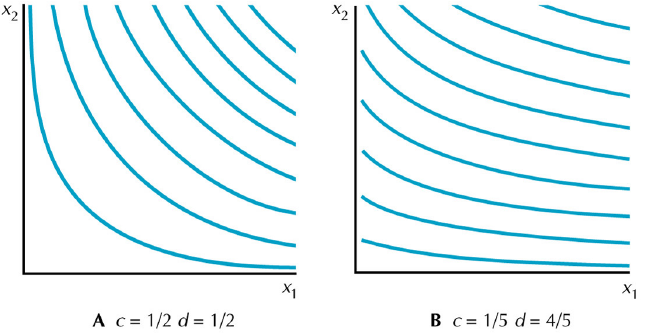
Cobb-Douglasovy preference

• Nejjednodušší užitková funkce, která generuje rozumné (well-behaved) preference (viz Figure 4.5).

• Užitková funkce má tvar u(x₁,x₂) = x₁^bx₂^c.

• Výhodné používat transformaci

nebo

Mezní užitek

Mezní užitek (MU) je změna užitku z nárůstu spotřeby jednoho statku, zatímco množství ostatních statků je konstantní.

Parciální derivace - derivace u(x₁, x₂) podle x₁, zatímco x₂ zůstává

stejné — zacházíme s ním jako s konstantou.

Příklady:

Důležité: Velikost mezního užitku závisí na tom, jakou užitkovou funkci (monotónní transformaci) si zvolíme.

• Když vynásobíme užitkovou funkci 2x, i mezní užitek se zvýší 2x => hodnota mezního užitku nemá žádný význam.

• Ale MU je úzce svázaný s MRS a tento pojem je užitečný.

Vztah mezi MU a MRS

Chceme změřit MRS = sklon indiferenční křivky u(x_i,x₂) = k, kde k je konstanta.

Zajímá nás taková změna (Ax_i, Ax₂), pro kterou bude užitek konstantní. Tedy

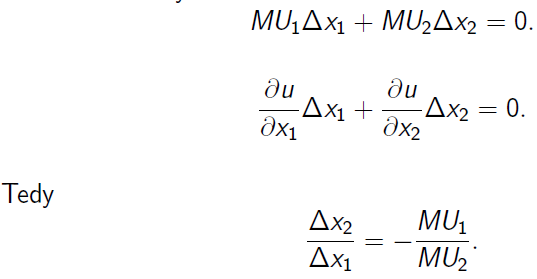
MRS umíme spočítat z užitkové funkce.

Příklad: Užitek z dojíždění

Otázka: Jet do práce autobusem nebo autem?

Každý způsob dopravy představuje koš různých charakteristik:

např. x₁ je doba jízdy do práce autem, y₁ je doba jízdy do práce autobusem, x₂ je náklad auta, atd.

Předpokádáme, že užitková funkce má lineární tvar U(x₁,..., x_n) = B₁x₁ + ... + B_nx_n.

Potom můžeme z pozorovaných rozhodnutí lidí statisticky odhadnout parametry B_i, které nejlépe popisují tato rozhodnutí.

Příklad: Užitek z dojíždění (pokračování)

Domenich a McFadden (1975) odhadli následující užitkovou funkci:

U(TW, TT, C) = -0.147TW - 0.0411 TT - 2.24C,

kde TW = celkový čas chůze k a od autobusu/auta v minutách,

TT = celkový čas jízdy v minutách,

C = celkové náklady na cestu v dolarech.

Jakmile máme užitkovou funkci, můžeme ji použít k řadě účelů:

• Můžeme spočítat mezní míru substituce mezi dvěma charakteristikami.

• Můžeme předpovědět reakci zákazníků na změnu ve veřejném dopravním systému.

• Můžeme odhadnout, jestli je navrhovaná změna prospěšná (cost-benefit analysis).

Shrnutí

• Užitková funkce je způsob reprezentace preferencí. Číslené hodnoty užitku přiřazené k různým spotřebním košům nemají samy o sobě žádný význam.

• Libovolná monotónní transformace užitkové funkce popisuje stejné preference.

• Mezní míra substituce

()

13 / 1