10.3* План швидкостей

Залежність між швидкостями точок плоскої фігури (10.4) дозво­ляє визначити швидкості точок цієї фігури простою побудовою, що називається планом швидкостей.

Планом швидкостей називається діаграма, на якій, від деякого центра, відкладені вектори швидкостей тіла.

a) б)

Рис. 10.6

Нехай швидкості точок А, В, С плоскої фігури (10.6 а). Тоді відповідний план швидкостей одержимо, відклавши від деякого центра О в певному масштабі відрізки:

(рис. 10.66)

Встановимо властивості і правила побудови плану швидко­стей. За 10.4 маємо:

Але з ∆ Оаb видно, що , або

Порівнюючи цей результат з ( ) , одержимо, що

,

Аналогічно .

Тоді, за ( ) маємо:

Крім того, за тою ж формулою:

і т.д.

Звідки

Отже:

1. Відрізки, що з'єднують кінці векторів на плані швидкостей перпендикулярні відрізкам, що з'єднують відповідні точки плоскої фігури і за модулем пропорційні цим відрізкам.

2. Фігури, позначені на плані швидкостей однаковими буква­ми, будуть при цьому подібні фігурам плоскої фігури і повернуті одна відносно другої на 90°.

Для побудови плану швидкостей точок плоскої фігури необ­хідно знати модуль і напрямок швидкості однієї з точок цієї фігури і пряму, по якій направлена швидкість якої-небудь точки фігури.

План швидкостей механізму будується як сукупність планів швидкостей окремих його ланок (тіл), причому всі вектори швидко­стей відкладаються від спільного центра О .

Приклад:

Кривошип ОА обертається з постійною кутовою швидкістю ω (рис. 10.7). Знайти швидкості також А i В .

Рис. 10.7

1. Знаходимо швидкість точки А : .

2. Проводимо з полюса О плану швидкостей в масштабі вектор

3. З кінця вектора проводимо перпендикулярну шатуну АВ пряму до перетину в точці b з прямою ob , проведеної з полюса паралельно швидкості точки В .

Одержуємо .

Відношення - кутова швидкість шатуна.

10.4. Миттєвий центр швидкостей і способи його визначення. Поняття про центроїди

Миттєвим центром швидкостей називається точка плоскої фігури, швидкість якої в даний момент часу дорівнює нулю.

Припустимо спочатку, що така точка існує. Прийнявши цю точку Р за полюс, можна знайти швидкість довільної точки А (рис. 10.8).

(10.5)

тому що

Звідси випливає, що швидкості точок при плоскому русі роз­поділяються точно так, як і при чисто обертовому русі. Роль нерухомої осі відіграє миттєва вісь, що проходить через миттєвий центр швидко­стей Р перпендикулярно площині креслення. Таким чином, швидко­сті всіх точок фігури перпендикулярні відрізкам, що з'єднують ці то­чки з миттєвим центром швидкостей , а величини швидко­стей пропорційні відстаням до миттєвого центру швидкостей.

Рис. 10.8

^{(10.5 а)}

Якщо швидкість точки А відома, то для визначення швидкості точки В можна використати співвідношення , звідки маємо .

Кутова швидкість плоскої фігури дорівнює швидкості будь-якої точки фігури, поділеної на відстань цієї точки до миттєвого центра швидкостей, наприклад .

Доведемо теорему про існування миттєвого центра швидко­стей.

Теорема

Якщо миттєва кутова швидкість плоского руху фігури не до­рівнює нулю, то миттєвий центр швидкостей існує.

Нехай швидкість довільної точки А плоскої фігури не до­рівнює нулю (в протилежному випадку точка А була б миттєвим центром швидкостей). Відкладемо від точки А відрізок перпендикулярний швидкості в напрямку обертання фігури навко­ло полюса.

На рис. 10.9 припускається, що , і тому відрізок АР відкладений від проти ходу годинникової стрілки. Доведемо, що швидкість точки Р дорівнює нулю, тобто ця точка є миттєвим центром швидкостей.

Рис. 10.9

В відповідності з формулою (10.4) маємо:

Оскільки швидкість перпендикулярна АР , то вона пара­лельна . Крім того, у відповідності з правилом побудови відрізка АР , ці два вектори ( I ) і мають протилежні напрями

Величина

Два вектори, рівні за величиною і протилежні за напрямком, в сумі дорівнюють нулю. Отже,

)

що і необхідно було довести.

Використовуючи основні властивості миттєвого центра швид­костей, можна знайти його положення і в інших випадках. На рис. 10.9,а показано, як знаходиться ця точка, коли відомі напрямки швидкостей двох точок. З точок проводяться перпендикуляри до век­торів i . Точка Р знаходиться на їх перетині.

Рис. 10.10

Якщо швидкості точок паралельні і , то для визначення миттєвого центра швидкостей слід використати властивості пропорціональності величин швидкостей відстаням точок до миттєво­го центра швидкостей.

На рис 10.10,6 і 10.10,в показано як знаходиться точка Р в цьому випадку.

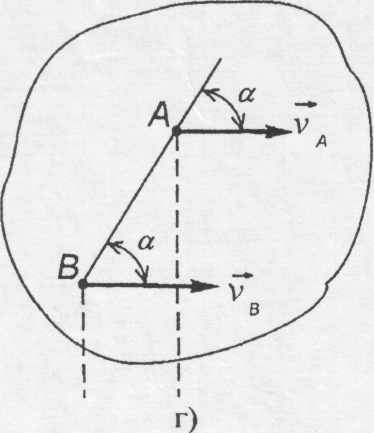
г) д)

Рис. 10.10

Якщо швидкості точок А і В плоскої фігури паралельні одна од­ній, а лінія АВ не перпендикулярна до лінії дії векторів і (рис 10.10,г), то миттєвий центр швидкостей лежить в нескінченності і швидко­сті всіх точок паралельні . При цьому з теореми про проекції швидко­стей випливає, що , тобто . Аналогічний результат одержимо для всіх інших точок. Отже, в цьому випадку швидко­сті всіх точок фігури в даний момент часу рівні одна одній за модулем і за напрямком. Такий стан тіла називають миттєво поступальним. Кутова швидкість тіла ω в цей момент часу дорівнює нулю.

Нарешті, є ще один тип задач, коли положення миттєвого центра швидкостей можна визначити зразу. Мова іде про кочення без ковзання одного тіла відносно іншого. В цьому випадку точка дотику Р (рис. 10.10, д) є миттєвим центром швидкостей.

При русі плоскої фігури в її площині миттєвий центр швидко­стей переміщується від однієї точки фігури до іншої, займаючи все нові і нові положення.

Геометричне місце миттєвих центрів швидкостей (траєкто­рія), відміченнях на площині, жорстко зв'язаній з плоскою фігурою називається рухомою центроїдою.

Геометричне місце миттєвих центрів швидкостей (траєкто­рія), відмічених на нерухомій площині, називається нерухомою центроїдою.

Наприклад, розглянемо кочення без ковзання колеса по нерухомій площині (рис. 10.11).

Рис. 10.11

В цьому випадку, нерухомою центроїдою є пряма АВ, рухо­мою - коло колеса. В кожний момент часу рухома і нерухома центрої­ди мають спільну точку - миттєвий центр швидкості Р , тобто точку, швидкість якої дорівнює нулю. Тому плоский рух можна подати як кочення без ковзання рухомої центроїди по нерухомій.