9.3. Обертальний рух твердого тіла навколо нерухомої осі

Рух твердого тіла, що має дві нерухомі точки, називається обертальним навколо нерухомої осі, а пряма, яка проходить через ці нерухомі точки, називається віссю обертання (рис. 9.3).

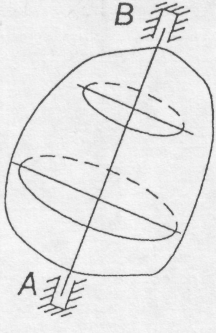
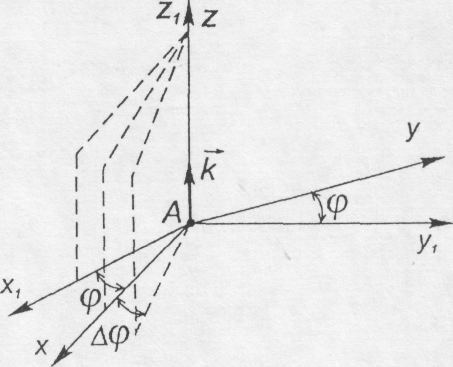
Рис. 9.3 Рис. 9.4

Точки тіла, які не лежать на осі обертання, рухаються в площинах, перпендикулярних до цієї осі, описують кола, центри яких лежать на осі. Відстань точки тіла від осі обертання називається раді­усом обертання.

Для визначення положення тіла проведемо через вісь обертан­ня дві площини: нерухому площину Ах₁y₁ і рухому площину Axz, жорстко зв'язану з тілом (рис. 9.4).

При обертанні тіла, площина Axz обертається з ним і кут між площинами змінюється. Двогранний кут між нерухомою і рухомою площинами називається кутом повороту тіла.

Для однозначного визначення положення тіла введемо в роз­гляд одиничний вектор , направлений по осі обертання. Будемо вважати, що кут φ зростає, якщо з кінця вектора ми бачимо обер­тання тіла, що відбувається проти стрілки годинника, і спадає - якщо бачимо обертання тіла за стрілкою годинника.

Таким чином, положення твердого тіла, що обертається навко­ло нерухомої осі, повністю визначається одним параметром

(9.5)

де - відома функція часу.

Співвідношення називається кінематичним рівнянням руху тіла, що обертається навколо нерухомої осі.

Кут повороту тіла, який відповідає числу п обертів, обчислю­ється за формулою:

(9.6)

де φ вимірюється в радіанах.

Введемо тепер поняття про кутову швидкість і кутове приско­рення тіла.

Нехай в момент часу t кут між нерухомою і рухомою площи­нами дорівнює , а в момент часу (рис. 9.4). Це означає, що за проміжок часу рухома площина, а отже, і тіло повер­нулось на кут

Відношення кута повороту до проміжку часу , називаєть­ся середньою кутовою швидкістю:

Границя цього відношення при називається кутовою швидкістю в даний момент чacу:

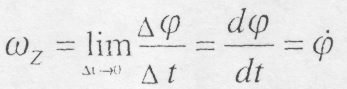^(9.7)

Введений в позначення кутової швидкості індекс Z підкреслює, що кутова швидкість може бути як додатною так і від'ємною в залежності від закону зміни кута .

Абсолютне значення кутової швидкості будемо позначати че­рез ω , тобто,

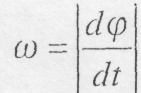
Якщо кут повороту змінюється в радіанах, то розмірність ку­тової швидкості буде:

В техніці часто кутову швидкість при обертанні тіла з по­стійною кутовою швидкістю вимірюють кількістю обертів за хвили­ну. Залежність між кутовою швидкістю і кількістю обертів за хвили­ну визначається формулою:

де n - кількість обертів за хвилину.

Нехай тепер в момент часу t кутова швидкість обертання дорівнює , а в момент зміна кутової швидкості в проміжок часу буде . Тоді за

Середнім кутовим прискоренням будемо називати відношен­ня зміни кутової швидкості до проміжку часу, за який ця зміна відбу­лася, тобто,

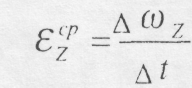
Границя цього відношення при називається кутовим прискоренням в даний момент часу:

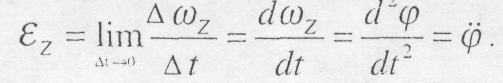^(9.8)

Кутове прискорення, характеризуючи зміну кутової швидко­сті за одиницю часу, дорівнює похідній від кутової швидкості за ча­сом або другій похідній за часом від кута повороті:

Розмірність кутового прискорення .

Досить корисним для подальшого вивчення кінематики твер­дого тіла є введення поняття вектора кутової швидкості і вектора кутового прискорення.

Вектором кутової швидкості твердого тіла, що обертаєть­ся навколо нерухомої осі, будемо називати вектор, чисельно рівний абсолютному значенню похідної за часом від кута повороту тіла і направлений вздовж осі обертання в той бік, звідки з його кінця вид­но поворот тіла, що проходить проти годинникової стрілки.

Нами вже був введений одиничний вектор . Якщо вектори направлені в один бік, то , якщо вони направлені в протилежні сторони, то .

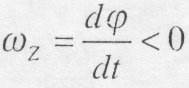Звідси випливає, що вектор кутової швидкості можна визна­чити за формулою:

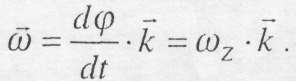^(9.9)

Вектором кутового прискорення будемо називати вектор, що дорівнює похідній за часом від вектора кутової швидкості, тобто

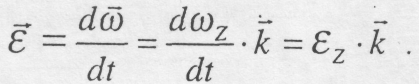^(9.10)

де

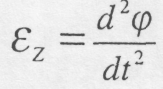
З формули (9.10) випливає, що вектор направлений як і вектор , вздовж осі обертання.

Абсолютне значення кутового прискорення будемо познача­ти через ε , тобто

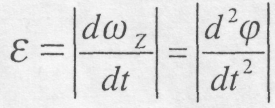
З формул (9.9) і (9.10) випливає, що кутова швидкість і кутове прискорення є відповідно проекціями векторів кутової швидкості і кутового прискорення на вісь Z.

Якщо і мають один знак, то обертання тіла прискорене, якщо різні знаки , то сповільнене, або якщо вектори і направ­лені в бік, то обертання тіла прискорене, якщо в протилежні боки - сповільнене.

Перейдемо тепер до знаходження швидкості і прискорення будь-якої точки тіла, що обертається навколо нерухомої осі.