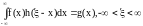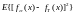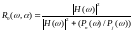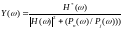Методы дереверберации звуковых сигналов

Ю.В. Ягунова

ВПО «Уральский государственный технический университет – УПИ»

РИ Радиотехнический факультет

Кафедра радиоэлектроники информационных систем

г. Екатеринбург, гр. Р-43043 julia-86@mail.ru

Существующие методы восстановления чёткости изображений применимы также и для дереверберации звуковых сигналов.

1. Метод дереверберации звуковых сигналов на основе фильтра Винера

В задаче восстановления звуковых сигналов, искаженных однородной линейной системой, исходное уравнение приводится к уравнению типа свертки.

(1.0)

Д ля получения устойчивого решения необходимо умножить подынтегральное выражение на некоторую функцию которая называется стабилизирующим множителем. Определим вид стабилизирующего множителя R в случае, когда в задачах восстановления изображений используется дополнительная информация о некоторых статистических характеристиках изображения и шума.

П 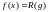усть — точное решение уравнения свертки с пра­вой частью . Полагаем, что , где n(х) —случайный шум. Таким образом, считаем, что g(x) есть реализация случайного процесса и, следовательно, приближенные решения являются также реализациями случайной функции.

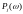
Б 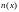удем также считать, что функции и являются реализациями стацио­нарных, некоррелированных между собой случайных про­цессов, а информация о характеристиках этих процессов представлена в виде их спектральных плотностей, которые будем обозначать соответственно и .

Среди операторов R(g) будем искать такой, который минимизирует величину

(1.1)

Следовательно

(1.2)

Передаточная функция восстанавливающего фильтра имеет вид

(1.3)

Выражение является передаточной функцией оптимального фильтра Винера

К достоинствам восстановления изображения с помощью фильтра Винера является простота его реализации. К недостаткам линейного метода относится усиление шума в изображении. Т.е. использование этих методов оправдано в случае не слишком сильной зашумленности изображения

Фильтр Винера является наилучшим среди возможных фильтров, когда осуществляется фильтрация по критерию минимума среднеквадратичной ошибки.

К тезисам прилагаются примеры (звуковые файлы К_ЭлизеФВшум(40), К_ЭлизеФВшум(150), К_ЭлизеФВшум(итог)(40), К_ЭлизеФВшум(итог)(150) ), в которых эксперименты проводятся над отрывком произведения Л.В. Бетховена для фортепиано «К элизе» (6 секунд). На изначальную мелодию накладываюся три её копии: с задержками 10 мс и 12 мс, и амплитудами 0.8А и 0.6А соответственно, где А – амплитуда эталонного сигнала. Для одного примера отношение сигнал/шум равно 40, для другого – 150. Также, хорошие результаты дали эксперименты с двенадцатью задержками, и со «смазом» 1.3 сек, имитирующим сильную гулкость помещения.