
6.4. Геометрическая интерпретация преобразований Лоренца.
Рассмотрим преобразования Лоренца с помощью геометрического метода, развитого Г. Минковским (1908 г.).
Диаграммы Минковского.
Пусть
имеются две ИСО:
система
и
система,
движущаяся относительно нештрихованной
с постоянной скоростью
![]() ,
при чем так, что в момент времени
,
при чем так, что в момент времени
![]() координатные оси этих систем совпадают.
Чтобы сделать рассмотрение наглядным
снова воспользуемся для построения
диаграмм пространства-времени сечением
четырехмерного пространства в плоскости
координатные оси этих систем совпадают.
Чтобы сделать рассмотрение наглядным
снова воспользуемся для построения
диаграмм пространства-времени сечением
четырехмерного пространства в плоскости
![]() (
(![]() ,
,
![]() ,
).
По оси абсцисс диаграммы традиционно
откладываем значения пространственной
координаты, а по оси ординат – величину
,
).
По оси абсцисс диаграммы традиционно
откладываем значения пространственной
координаты, а по оси ординат – величину
![]() ,
где
– скорость света. Обе оси проградуируем
в метрах, причем в одном и том же масштабе.
,
где
– скорость света. Обе оси проградуируем
в метрах, причем в одном и том же масштабе.
Начнем с построения диаграммы для системы.
Каждая
точка диаграммы характеризует некоторое
событие
![]() и называется мировой
точкой.
Всякой частице, даже неподвижной, на
этой диаграмме соответствует мировая
линия.
Например, ось
и называется мировой
точкой.
Всякой частице, даже неподвижной, на
этой диаграмме соответствует мировая
линия.
Например, ось
![]() -
это мировая линия частицы, покоящейся
в точке
.
Ось
-
это мировая линия частицы, покоящейся
в точке
.
Ось
![]() изображает совокупность всех событий,
одновременных с событием
.
изображает совокупность всех событий,
одновременных с событием
.
Мировая
линия, соответствующая распространению
света из точки
в положительном направлении оси
,
представляет собой биссектрису
![]() прямого угла.
прямого угла.
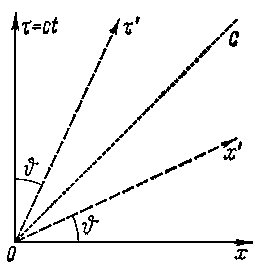
Теперь
изобразим на этой диаграмме оси
![]() и
и
![]() системы
отсчета.
системы
отсчета.
Мировую
линию начала отсчета
системы
получим, положив в преобразованиях
Лоренца
![]() .
.
![]() .
.
Тогда
![]() ,
(6.13)
,
(6.13)
где![]() ,
как обычно.
,
как обычно.
Уравнение
(6.13) есть уравнение прямой, которая
составляет с осью
угол
,
определяемый из условия
![]() .
.
Полученная
прямая – мировая
линия –
представляет собой совокупность всех
событий, происходящих в начале отсчета
системы,
т.е. ось![]() .
.
Ось системы – это прямая, изображающая все события, одновременные в системе с событием . Положив в преобразованиях Лоренца
![]()
![]() ,
получим
,
получим
![]() ,
или
,
или
![]() .
(6.14)
.
(6.14)
Отсюда следует, что ось составляет с осью тот же угол ( ), что и между осями и .
Таким
образом, оси
и
системы
расположены симметрично по отношению
к мировой линии света
,
и координатная сетка
системы
(
,
)
оказывается косоугольной. Чем больше
скорость
системы,
тем более «сплющенной» будет её
координатная сетка, а при
![]() она
вырождается в мировую линию света.
она
вырождается в мировую линию света.
И последнее, что необходимо сделать на диаграмме, - это проградуировать оси , и , обеих систем отсчета. Проще всего это сделать, воспользовавшись инвариантностью интервала:
![]() .
.
Отметим
на оси
системы
точку, соответствующую единице времени
в
системе
(![]() ).
Проведем через эту точку гиперболу
).
Проведем через эту точку гиперболу
![]() ,
,
все
точки которой отвечают инвариантному
интервалу
![]() (при
(при
![]() и
).
Её асимптотой является мировая линия
света.
и
).
Её асимптотой является мировая линия
света.
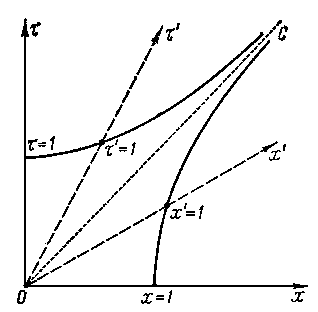
Точка пересечения этой гиперболой оси соответствует единице времени в системе. Действительно,
![]() ,
и при
,
и при
![]() .
.
Аналогично
градуируются оси
и
:
возьмем в
системе
точку
![]() ,
,
![]() и проведем через неё гиперболу
и проведем через неё гиперболу
![]() .
Тогда точка пересечения её с осью
,
где
.
Тогда точка пересечения её с осью
,
где
![]() ,
дает единицу длины (
,
дает единицу длины (![]() )
в
системе
(т.к.
)
в
системе
(т.к.
![]() и
,
то
).
и
,
то
).
Построенная
таким образом диаграмма – диаграмма
Минковского
– соответствует переходу от
к
системе отсчета и отвечает преобразованиям
Лоренца. В согласии с принципом
относительности
для обратного перехода от
![]() к
системе
диаграмма будет иметь совершенно
симметричный вид: у
системы
координатная сетка будет прямоугольной,
а у
системы
– косоугольной.
к
системе
диаграмма будет иметь совершенно
симметричный вид: у
системы
координатная сетка будет прямоугольной,
а у
системы
– косоугольной.
Диаграмма Минковского позволяет просто и наглядно интерпретировать такие релятивистские эффекты, как относительность понятия одновременности замедление времени и лоренцево сокращение.
Относительность понятия одновременности следует непосредственно из рисунка.
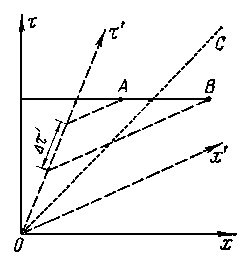
Действительно
события
и
![]() ,
одновременные в
системе,
в системе
оказываются
неодновременными. Событие
произойдет позже события
на время
,
одновременные в
системе,
в системе
оказываются
неодновременными. Событие
произойдет позже события
на время
![]() .
.
Замедление времени.
Рассмотрим
часы
и
,
которые показывали одинаковое время
![]() в момент, когда они находились в одной
точке пространства (
в момент, когда они находились в одной
точке пространства (![]() .
Предполагается, что часы
неподвижны в
системе,
а часы
– в
системе
отсчета.
.
Предполагается, что часы
неподвижны в
системе,
а часы
– в
системе
отсчета.
Пусть по часам прошла единица времени ( ); это отвечает событию на диаграмме.
Проведем
через точку
гиперболу
и прямую
![]() ,
характеризующую все события, одновременные
в
системе
с событием
.
Пересечение оси
(мировой линии часов
)
с гиперболой
,
характеризующую все события, одновременные
в
системе
с событием
.
Пересечение оси
(мировой линии часов
)
с гиперболой
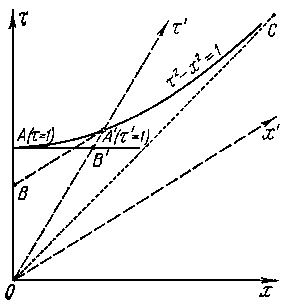
дает
точку
![]() (
(![]() ,
а с прямой
,
а с прямой
![]() –
точку
–
точку
![]() (
(![]() .
Это значит, что в
системе
в момент, когда по часам
уже прошла единица времени, по движущимся
часам
единица времени ещё не прошла, т.е. часы
идут замедленно.
.
Это значит, что в
системе
в момент, когда по часам
уже прошла единица времени, по движущимся
часам
единица времени ещё не прошла, т.е. часы
идут замедленно.
С
помощью этой же диаграммы убедимся, что
эффект замедления времени является
обратимым. Проведем прямую
![]() ,
параллельную оси
,
которая характеризует все события,
одновременные в
системе с событием
(
.
,
параллельную оси
,
которая характеризует все события,
одновременные в
системе с событием
(
.
Точка
пересечения
прямой
с мировой линией часов
системы
(осью
)
показывает, что
![]() т.е.,
в самом деле, по отношению к
системе
замедленно идущими оказываются теперь
часы
системы.
т.е.,
в самом деле, по отношению к
системе
замедленно идущими оказываются теперь
часы
системы.
Лоренцево сокращение.
Пусть
метровый стержень покоится в
системе
(отрезок
![]() ).
Мировые линии его концов – это прямые
).
Мировые линии его концов – это прямые
![]() и
и
![]() .
.
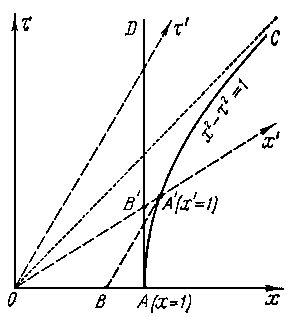
Чтобы
измерить длину этого стержня в
системе,
надо зафиксировать координаты его
концов одновременно
в этой системе. Но в
системе
одновременным с событием
или
![]() (фиксированием левого конца стержня)
является событие
– точка пересечения мировой линии
правого конца стержня с линией
одновременности
(фиксированием левого конца стержня)
является событие
– точка пересечения мировой линии
правого конца стержня с линией
одновременности
![]() .
Из диаграммы видно, что в
системе
.
Из диаграммы видно, что в
системе
![]() ,
т.е. движущийся относительно
системы
стержень будет короче одного метра.
,
т.е. движущийся относительно
системы
стержень будет короче одного метра.
Так
же просто можно показать, что и лоренцево
сокращение является обратимым. Если
метровый стержень покоится в
системе
(отрезок
![]() ),
то, проведя мировые линии его концов в
этой системе (О
и
),
то, проведя мировые линии его концов в
этой системе (О
и
![]() ),
увидим, что в
системе
при одновременном измерении его концов
отрезок
),
увидим, что в
системе
при одновременном измерении его концов
отрезок
![]() ,
т.е. по отношению к
системе
лоренцево сокращение будет испытывать
стержень.
,
т.е. по отношению к
системе
лоренцево сокращение будет испытывать
стержень.
