2.2.3 Производящая функция вероятностей
Математическое ожидание и дисперсию дискретной случайной вели-
чины с целыми неотрицательными значениями удобно находить с помощью
производящей функции вероятностей.
Определение производящей функции вероятностей.
Производящей функцией вероятностей называется конечная сумма
n ∞
ϕ(x) = ∑ pkxkили сумма степенного ряда ϕ(x) = ∑ pkxk.
k=0
k=0
Коэффициенты pkв данных суммах есть вероятности pkдискрет-
ной случайной величины X с конечным P (X = k) = pk, k = 0, 1, 2, . . . , n
или счетным P (X = k) = pk, k = 0, 1, 2, . . . рядом распределения.
∞
Степенной ряд в точке x = 1 равен числовому ряду ϕ(x) =
∑
k=0
pk,
сходящемуся к единице в силу аксиом счетной аддитивности и нормирован-
∞
ности. При значениях |x| ≤ 1 степенной ряд ϕ(x) = ∑ pkxkмажорируется
k=0
∞
числовым рядом
∑ pk, что обуславливает абсолютную и равномерную схо-
k=0
димость данного степенного ряда. Отсюда следует возможность вычисления
производных первого, второго и высших порядков от производящей функции
путем почленного дифференцирования соответствующих степенных рядов.
40
Если производящая функция вероятностей равна конечной сумме, то
ее также можно почленно дифференцировать.
Первая и вторая производные производящей функции ϕ(x) для счет-
ной дискретной случайной величины имеют следующий вид:
ϕ0(x) = ∑k· pk· xk−1=p1+ 2p2x + 3p3x2+ . . . ,
k
00
ϕ (x) = ∑k· (k − 1) · pk· xk−2= 2p2+ 6p3x + . . . .
k
Аналогичный вид имеют первая и вторая производные производящей функ-
ции и для конечной дискретной случайной величины.
Отсюда, значение первой производной производящей функции вероят-
ностей при значении переменной x = 1 равно ϕ0(1) = ∑ k · pkи совпадает
k
с математическим ожидинием случайной величины, так что ϕ0(1) = mx.
Значение второй производной производящей функции при x = 1 равно
00
ϕ (1) = ∑k· (k − 1) · pk= ∑k2pk − ∑k· pk= α2− mx.
k
k
k
Ранее было доказано, что дисперсия выражается через второй началь-
ный момент α2и математическое ожидание mxпо формуле Dx= α2− m2x.
Отсюда и предшествующих формул выводится представление диспер-
сии через значения ϕ0(1) , ϕ00(1) в виде Dx= ϕ00(1) + ϕ0(1) − [ϕ0(1)]2.
Таким образом, математическое ожидание и дисперсия дискретной слу-
чайной величины выражаются через первую и вторую производные произво-
дящей функции вероятностей следующим образом:
00
0
0
mx= ϕ0(1), Dx= ϕ (1) + ϕ (1) − [ϕ (1)]2.
Пример. Найдем математическое ожидание и дисперсию распределе-
ния Бернулли с помощью производящей функции.
Производящая функция распределения Бернулли имеет вид
n
ϕ(x) =
∑
k=0
pkxk= q · x0+ p · x1= q + px.
Отсюда, ϕ0(x) = p , ϕ00(x) = 0 , ϕ0(1) = p , ϕ00(1) = 0 .
Используя формулы вычисления математического ожидания и диспер-
сии через производные производящей функции, получим окончательно:
00
0
0
mx= ϕ0(1) = p, Dx= ϕ (1) + ϕ (1) − ϕ (1)2= 0 + p − p2= p (1 − p) = pq.
41
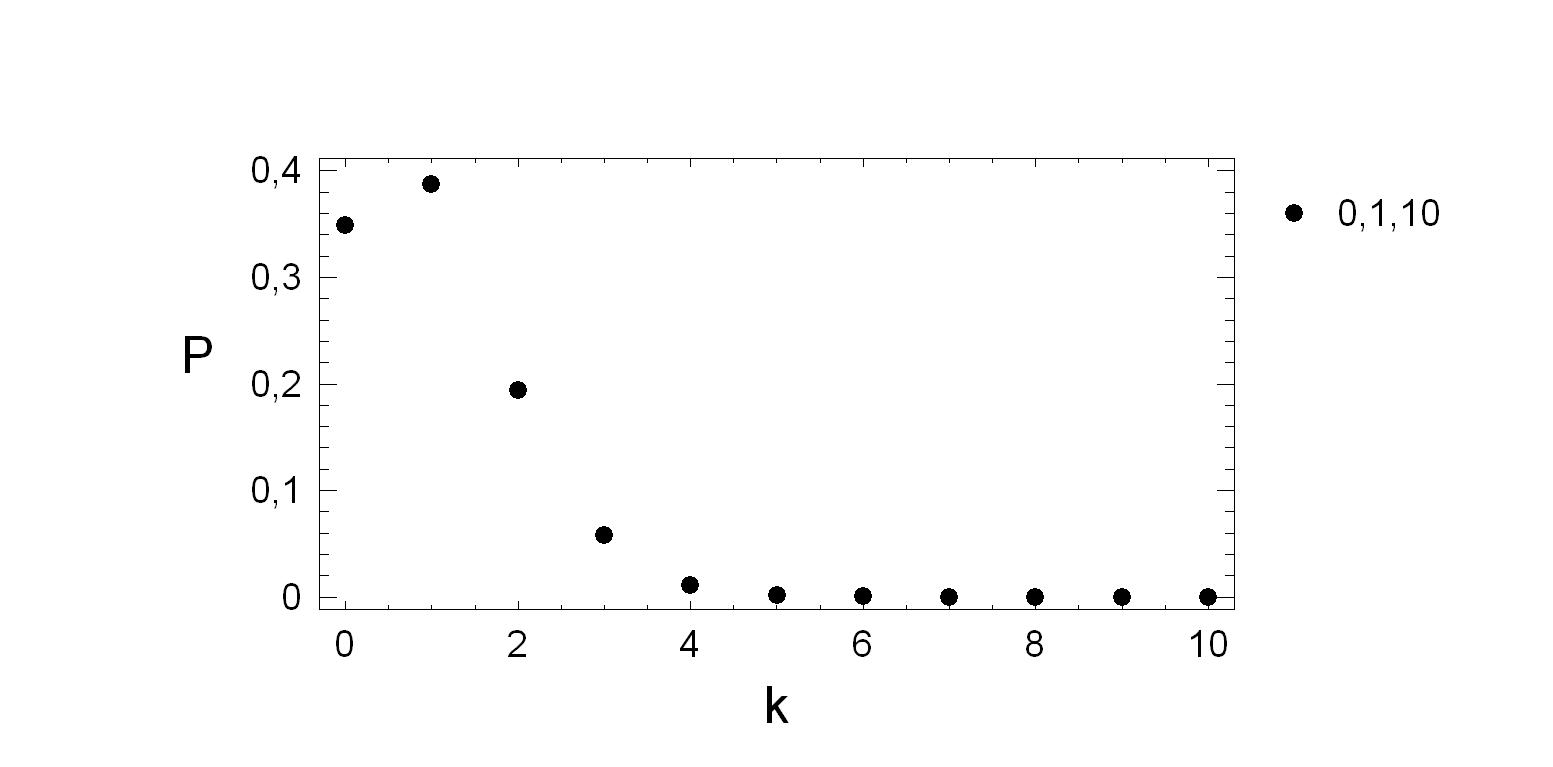
Приведём, в дополнение к уже рассмотренным, законы распределения и
числовые характеристики для тех дискретных случайных величин, которые
на практике и в теоретических исследованиях встречаются наиболее часто.