3.5. Определение направления главных осей инерции. Главные моменты инерции

В расчетах на прочность, жесткость и устойчивость в основном рассматриваются главные центральные оси инерции сечений, так как геометрические характеристики ( , , , , ) относительно этих осей входять в формулы для определения напряжений и деформации. Обозначим такие оси буквами u и v.

Д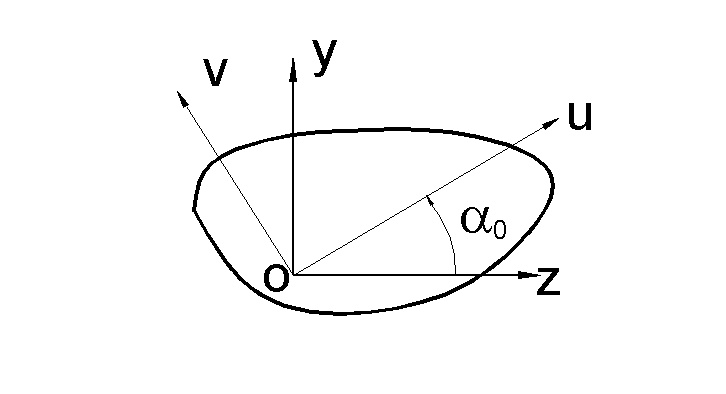 ля определения положения осей u и v для несимметричной фигуры (рис. 22) повернем произвольную исходную систему центральных осей zOy на некоторый угол ₀ , при котором центробежный момент инерции будет равняться нулю.

Следовательно

Рис.22

,

отсюда

, .

Полученные из последней формулы два значения угла ₀ отличаются между собой на 90° и дают положение двух главных осей. Под меньшим углом ₀ к оси Oz проводят главную ось Ou . Отрицательные углы ₀ откладывают по часовой стрелке, положительные  наоборот.

Главные моменты инерции  это моменты инерции относительно главных центральных осей. Их можно найти из общих формул перехода к повернутым осям (см. п. 3.4), взяв  =  ₀ :

Формулы перехода к повернутым на угол  осям zOy относительно главных осей имеют упрощенный вид, т. к.

Важно отметить, что главные моменты инерции имеют свойство экстремальности. В этом легко убедиться, если продифференцировать выражение для момента инерции I_z относительно произвольной оси по переменной  :

Следовательно, , если . Это значит, что моменты инерции относительно главных осей имеют экстремальные значения. Вспомним, что

,

то есть сумма моментов инерции относительно двух взаимно перпендикулярных осей  это величина постоянная. Отсюда делаем вывод, что относительно одной из главных осей момент инерции имеет максимальное значение где рассматриваемого сечения, а относительно другой  минимальное.