МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ М. В. ЛОМОНОСОВА

ФАКУЛЬТЕТ ПСИХОЛОГИИ

ОТЧЕТ

по общему психологическому практикуму

МЕТОД СРЕДНЕЙ ОШИБКИ

Тема: «Влияние местоположения эталона и начальной точки подравнивания на величину переменного стимула, а так же моторного компонента подравнивания переменного стимула к эталону на величину разностного порога»

Выполнила:

студентка 304 группы

факультета психологии

Бугрей Татьяна

Преподаватель:

Степанова О. Б.

МОСКВА, 2011

1. Теоретическое введение

Метод средней ошибки (МСО) был создан (взят из астрономии, где использовался для расчета удаленности неизвестной звезды по ее яркости) Фехнером для измерения дифференциальной чувствительности. Позднее он стал использоваться для измерения абсолютной чувствительности, хотя, по мнению Фехнера, МСО не позволяет прямо измерить порог; он дает меру, пропорциональную чувствительности. Позднее этот метод модернизировался, поэтому на данный момент существуют два понимания данного метода.

I Классический МСО Г.Фехнера

МСО— метод классической психофизики, в котором испытуемый сам устанавливает требуемую инструкцией величину стимула (напр., «стимул должен быть едва ощущаемым», «стимул должен едва заметно отличаться от др. стимула» или «стимул должен казаться равным др. стимулу» и т. д.). Синонимы: метод установки, метод воспроизведения, метод подравнивания. MСО разработан Г. Фехнером для измерения порогов и стал одним из основных в психофизике.

При использовании МСО для измерения дифференциального порога испытуемый изменяет переменный раздражитель, уменьшая или увеличивая его интенсивность, добиваясь, чтобы он перестал казаться отличающимся от др., заданного в качестве эталона (постоянного раздражителя). Т. о., при работе по МСО задача испытуемого сводится к тому, чтобы воспроизвести (или установить) величину эталона. Т. к. в каждой отдельной пробе он, как правило, не может воспроизвести эталон совершенно точно и останавливает свой выбор на каком-то ином раздражителе, можно считать, что, выполняя инструкцию сделать оба раздражителя одинаковыми, испытуемый допускает ошибку, которая им не замечается. Средняя арифметическая этих ошибок, вычисленная для всей серии проб, рассматривается как величина, субъективно соответствующая эталону.

Фехнер справедливо указывал, что, наряду с этой величиной, сенсорная способность испытуемого должна характеризоваться величиной разброса результатов, показанных в отдельных пробах вокруг своего среднего значения. Величина этого разброса, вычисленная как среднее отклонение от субъективного значения эталона (именно ее Фехнер и назвал средней ошибкой), принималась им за величину, прямо пропорциональную дифференциальному порогу, и использовалась как мера чувствительности в МСО.

В качестве статистических мер, необходимых для оценки пороговых показателей, в МСО принято характеризовать полученное распределение чаще всего средним арифметическим и реже — медианой. В качестве мер разброса используются стандартное отклонение и реже — полумежквартальный размах. Очень редко в настоящее время используется такая мера изменчивости полученных данных, как среднее отклонение или средняя ошибка:

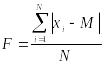
где x_i — одно из значений в ряду подравниваний; M — среднее арифметическое подравниваний (PSE- точка субъективного равенства); n — количество подравниваний.

По-видимому, Фехнер придавал такой психофизический смысл показателю разброса, что чем более расплывчат субъективный эквивалент эталонного стимула, чем меньше испытуемый может отличить его от соседних значений, тем ниже чувствительность. Фехнер для характеристики чувствительности, изображаемой графиком нормального распределения, испытуемого применял два критерия: расплывчатость графика подравниваний (статистической характеристикой которого является среднеквадратичное отклонение) и вершинность (математическое ожидание) этого графика. Понятно, что математическое ожидание графика распределения будет являться точка субъективного равенства, она же PSE. Для характеристики чувствительности, соответственно имеются два показателя:

∆= PSE - Sst

F=Ϭ

где PSE-точка субъективного равенства; Sst – величина эталонного стимула; F-феноменальная мера чувствительности – расплывчатость

Таким образом, ∆ соответствует величине константной ошибки (CE). А F объясняется тем, что чем ниже чувствительность испытуемого, тем более далекие стимулы он принимает за равные эталону, поэтому эти два разные показателя как бы характеризуют чувствительность с разных сторон, и потому оба имеют право на существование.

II Современный МСО

Т.к. инструкция, даваемая Фехнером испытуемому, не уточняла, какую именно точку в интервале неопределенности должен выбрать испытуемый, это стало проблемой метода. В связи с этим ряд исследователей (Челпанов, 1925; Осгуд, 1954; Торгерсон, 1958; Вудвортс и Шлосберг, 1965; Бардин, 1976) предлагают использовать в качестве меры чувствительности также и величину отстояния субъективного эквивалента эталона (центра распределения подравниваний) от эталона. Обосновывается это предложение тем, что чем ниже чувствительность испытуемого, тем более далекие стимулы он принимает равными эталону, поэтому эти два разные показателя как бы характеризуют чувствительность с разных сторон, и потому оба имеют право на существование. Вместе с тем никто из этих авторов не обращает внимания на то обстоятельство, что по смыслу введенных выше определений предлагаемая ими мера оценки чувствительности как разность значений точки субъективного равенства и эталона является константной ошибкой: CE = PSE - Sst .

Экспериментальными исследованиями показано, что константная ошибка определяется главным образом систематическими ошибками измерения, такими как пространственные (при зрительной стимуляции) и временные (при звуковой стимуляции) ошибки.

Для измерения границ интервала неопределенности, и, следовательно, разностного порога как половины интервала неопределенности, испытуемому должно быть указано на поиск точки первого равенства переменного стимула и эталона. В таком эксперименте, где подравнивание начинается от стимулов, заметно больших и заметно меньших, чем эталон, результаты подравнивания представляют собой бимодальное (двугорбое) распределение (рис. 1).

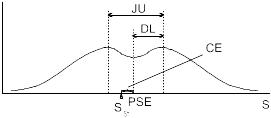
Рис. 1. Распределение результатов подравниваний испытуемым переменного стимула к эталонному при инструкции искать точку первого равенства и чередовании исходных значений изменения переменного стимула от заметно больших и заметно меньших, чем эталон: по оси абсцисс – величина стимула, по оси ординат – частота подравнивания стимула к стандартному

IU=Lh- Ll – интервал неопределености

DL= 1\2 IU – разностный порог

PSE= (Lh+ Ll)\2 – точка субъективного равенства

CE=PSE-Sst – константная ошибка

В случае измерения абсолютного порога чувствительности испытуемый регулирует величину стимула, первоначально вызвавшего отчетливое ощущение, до тех пор, пока не установит такое его значение, при котором он впервые утрачивает ощущение воздействия стимула. Если установка начинается с явно неощущаемой величины стимула, то испытуемый должен найти такое его значение, при котором ощущение впервые появляется. Обычно рекомендуется для оценки абсолютного порога использовать такие меры центральной тенденции, как медиана и среднее. Меры изменчивости (межквартильный размах и стандартное отклонение) в данном случае характеризуют только вариативность установок. В случае получения бимодального распределения за оценку абсолютного порога следует брать середину расстояния между двумя экстремумами аналогично определению точки субъективного равенства в задаче измерения разностного порога.

Цель: Определить влияние местоположения эталона и начальной точки подравнивания на величину переменного стимула, а так же моторного компонента подравнивания переменного стимула к эталону на величину разностного порога.

Задачи:

1)Определить пороговые показатели с помощью МСО ;

2)Установить влияние местоположения эталона на величину переменного стимула;

3)Установить влияние начальной точки подравнивания на величину переменного стимула;

4)Установить влияние моторного компонента на величину разностного порога, полученного в ММИ (Метод минимальных изменений) и МСО.

Гипотезы:

1)Среднее значение переменного стимула, полученное при расположении эталона слева, больше, чем среднее значение переменного стимула, полученное при расположении эталона справа;

2)Среднее значение переменного стимула, полученное при подравнивании от начальной точки больше эталонного стимула, будет больше, чем среднее значение переменного стимула, полученное при подравнивании от начальной точки меньше эталонного стимула;

3)Величина разностного порога, полученного в ММИ больше, чем величина разностного порога, полученного в МСО